消磁电流过渡过程对消磁效果的影响

陈文涛，张国友，张安明

（1．海军装备部沈阳军事代表局驻大连426厂代表室，辽宁大连116005; 2．海军工程大学电气与信息工程学院，湖北武汉 430033）

0 引言

舰船的综合消磁就是工作线圈中通以正负交变，幅值衰减的脉冲电流，在补偿线圈营造的无磁空间中对舰船进行无磁滞退磁［1，7－8］的过程。目前，在磁化效果的分析和建模中，都假定脉冲电流是理想的阶跃，忽略其上升的过渡过程（从0上升到最大幅值的时间），然后再基于铁磁学和电磁学理论来计算脉冲的最大幅值，确定幅值衰减率，通电频率及通断电时间等参数。然而，理想的阶跃在工程中并不可能实现，电流上升的过渡过程总是客观存在的，在实际消磁工作中，对工作电流的过渡过程也有具体的指标要求。过渡过程的存在对消磁效果是否会有一定的影响及这一指标是否合理尚无定论。

本文将通过理论分析和实验验证对这一问题展开研究。

1 不同电流产生的磁场对金属的磁化作用

众所周知，一切的电磁行为都遵循麦克斯韦方程组［2］，消磁时，低频交流线圈中的磁场属于磁准静态场，再依据金属的物质特性方程，可以得到磁场在金属中的传播规律为:

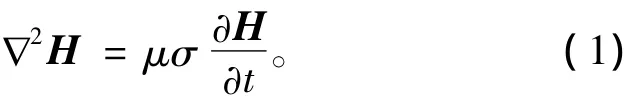
其中，μ和σ分别为磁导率和电导率，这是典型的扩散方程。

假设一种理想的位形，设铁磁物质充满半个空间，如图1所示。取一直角坐标系，令xy平面与铁磁物质的界面重合，z方向指向物质的内部，并假设物质外部的磁场H沿着x方向，即:

在所设条件下，物质内部磁场也必沿着x方向，且只是坐标z的函数［3］:

图1 半空间的铁磁物质Fig.1Ferromagnetic material full of semi-space

下面对3种不同制式的消磁电流对铁磁物质的磁化作用进行分析。

1.1 理想脉冲电流的磁化作用

由于外磁场由理想脉冲电流产生，所以设物质外部磁场的表达式为:

用拉普拉斯变换的方法求解上述方程，对式（5）和（6）进行拉普拉斯变换，得到如下方程:

式中:s为常量，且s和z是互相独立的变量，则满足边界条件式（8）和式（9）的解为

通过拉氏逆变换得到式（10）的时域表达式为

即:F（u）是t和z的二元复合函数。这里仅讨论以z为参数，F（u）随t的变化关系，即不同深度的H/H0随时间t的变化关系。对于造船钢板，取μ=500 μ0，σ=107西门子/m，选取3 mm，7 mm和10 mm等3种不同的深度，并且作用的时间都为10 s，通过Matlab编程仿真并绘图［4－6］，如图2所示。

图2 理想阶跃消磁电流在不同深度上的曲线Fig.2The ideal leap's magnetization effect in different depth

可见，不同深度上的磁场强度随时间的增加而上升，z越小，磁场强度上升越快，随着时间的增加，磁场强度上升趋势渐缓。

1.2 匀速上升电流的磁化作用

1.2.1 直接积分法

由于外磁场由匀速上升电流产生，所以设物质外部磁场的表达式为:

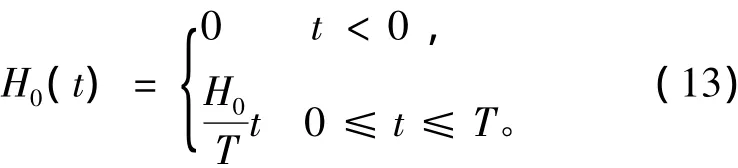
其中，T为电流作用的时间，将式（13）代入传导方程（5），并确定边界为:

初始条件为:

同样，用拉普拉斯变换的方法解此方程，可得:

如果能直接获得式（16）的时域表达式，便可进行相关的分析和计算，然而却是不容易办到的，必须另辟蹊径。

通过对式（16）变形可得:

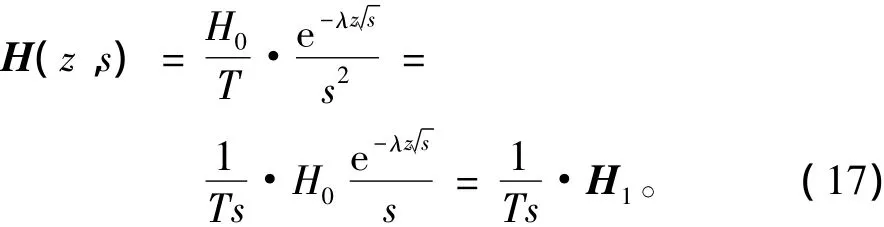
其中，H1即为式（10），再由拉氏变换的性质可知，只要对式（10）的时域表达式（11）在0～t内对t求一次积分，再乘以相应的系数，便可得到式（17）的时域表达式:

这样，可以据此式计算过渡过程内不同时间点不同深度上的磁场强度。暂时称其为直接积分法。

1.2.2 小阶跃叠加法

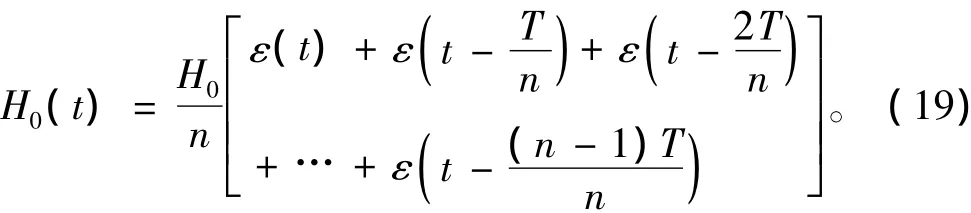
将式（13）的外磁场看成是由n个幅值相同（均为H0/n）、作用时间依次递减的小的理想阶跃组成，即:其中，ε（t）为理想阶跃函数，再利用式（11），采用叠加的方法可计算出过渡过程内不同时间点不同深度的磁场强度，n值越大，则计算精度越高。表1列出了5种深度，n从100，200直到10 000，2 s过渡时间结束时的H/H0值。

可见，剖分数n的值越大，小阶跃叠加法的计算值越接近直接积分计算值，当n取10 000时，叠加计算值已和直接计算值基本相同，从而验证了小阶跃叠加法的正确性。为分析梯形波的磁化效果打下基础。

为了能实时显示过渡过程内每个时间点的H/H0值，利用小阶跃叠加法，选3种不同的深度，分别为3 mm、7 mm和10 mm，过渡过程T设为2.5 s，Matlab数值仿真结果如图3所示。

图3 匀速上升电流不同深度的H/H0曲线Fig.3Equal up current's value of H/H0in different depth

同样可以看出，z越小，磁场上升越快，但是和图2对比明显看出，匀速上升电流的磁化效果远不如理想阶跃电流的磁化效果。

1.3 梯形波电流的磁化作用

梯形波电流是指先匀速上升一段时间，再维持一段时间不变的消磁电流。该电流最接近实际消磁工作中所用的消磁电流。假设有2种梯形波电流，通电时间均为2 s，最大幅值相同，1号梯形波的过渡过程时间为0.5 s，稳定时间为1.5 s;2号梯形波的过渡时间为1.0 s，稳定时间为1.0 s。如果用解析法进行分析，则式（5）会成为1个非齐次方程，特解的寻找非常困难。表2列出了用小阶跃叠加法仿真计算得到的这2种梯形波电流在5种不同深度的H/H0值。

可以看出，同样通电时间和幅值的梯形波电流，过渡时间越短的磁化效果越好。

24 种制式消磁电流磁化效果比较

上文单独分析了4种制式消磁电流对铁磁物质的磁化作用，为了便于比较，将通电制式参数进行调整，具体参数见表3。Matlab的动态仿真结果如图4所示。

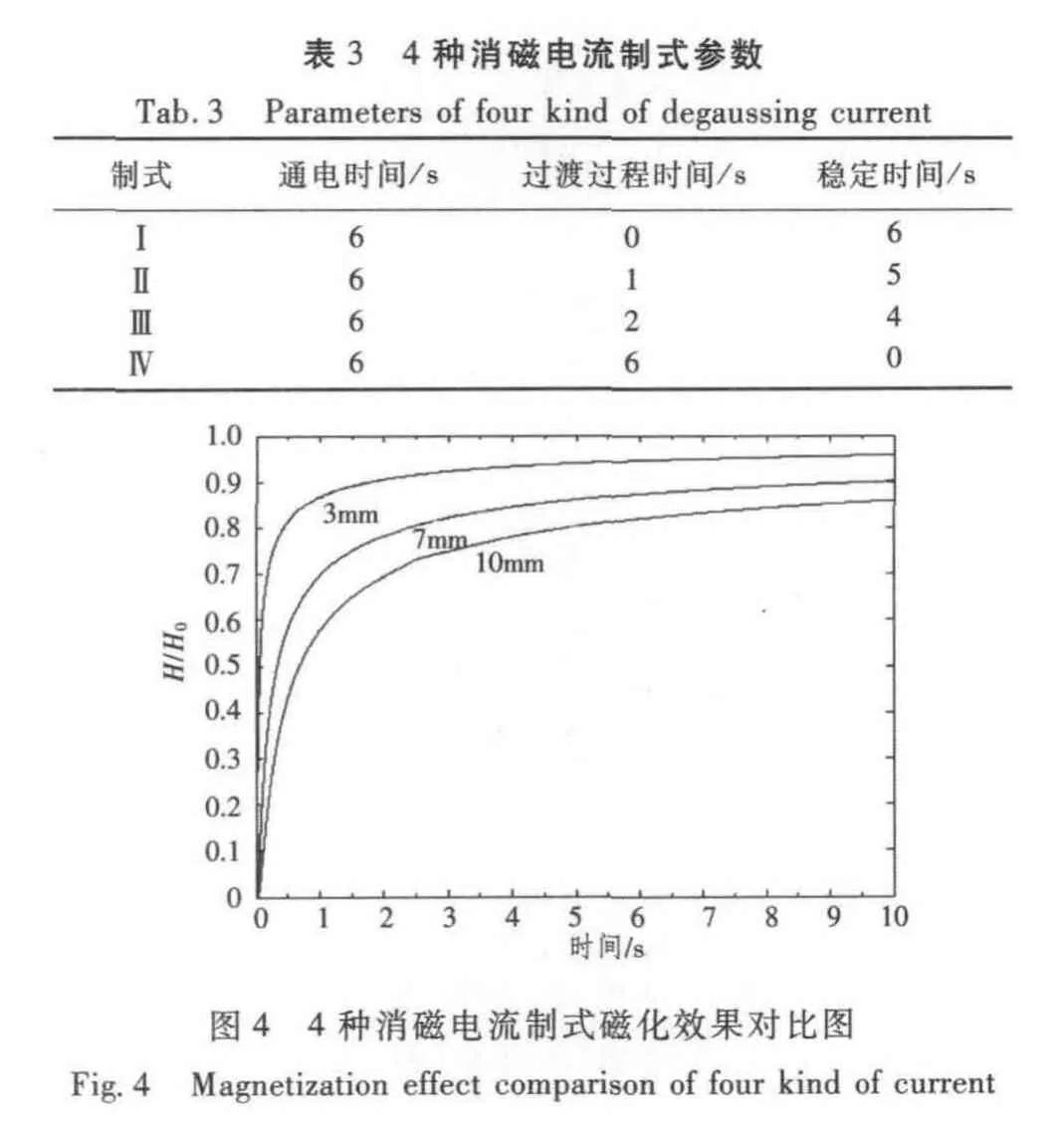
可以看出，匀速上升电流制式的磁化效果最差，梯形波相对于理想脉冲，在过渡过程有较明显差别，进入稳定阶段后，差别迅速减小，最后非常接近。

3 实验设计与结果分析

由于实时的磁化效果无法用实验验证，设计实验的目的主要是为了检验各种波形的消磁效果和结果磁场的稳定性。

首先设计制作了由计算机控制的可控电源系统，并开发了相应的控制软件，此系统可以输出参数可调的电流，这些参数包括脉冲个数、衰减模式，衰减比、上升时间、稳定时间、下降时间及断电时间等。

3.1 消磁实验

选用12 mm和20 mm两种厚度的钢板在北航向上进行消磁实验，通电时，消磁电流从小电流开始通起，以很小的幅度逐渐增加，反复通电和测量，直到结果磁场能达到消磁规范，这时认为找到了能否消磁的消磁电流的能量临界值，以此模式作为0号波，在此基础上对每一块钢板分别设定4种波形，波形的参数分别如表4和表5所示。其中，对12 mm板消磁时，首脉冲的幅值为6.4 A，脉冲个数均为36个，衰减模式为等差衰减，等差为0.17 A。对于20 mm钢板，首脉冲的幅值为22.2 A，脉冲个数为50个，衰减模式为等差衰减，等差为0.45 A。测量点均为21个。

通电结果表明，与每一块钢板对应的5种波形均可以达到消磁规范，消磁过程中还发现，对2块钢板均存在如下现象，即从0～3号波，由于过渡过程时间的增加，能量不断减小，通电时纵向补偿电流要不断增加，如对12 mm板消磁时从0～3号波纵向补偿依次为10 A，10 A，11 A和11 A。4号波由于能量最大，纵向补偿与0号波相同为10 A。这表明在消磁电流能量不充足时需要在纵向补偿的帮助下，才能使磁畴充分扭转，也证明了此时消磁电流的确处在临界状态。

3.2 结果磁场的稳定性实验

磁场稳定性定义为在外部磁场改变的情况下，钢板磁场变化的难易。在实验室条件下，通过在工作线圈中通以短时的脉冲电流来改变外部磁场，测量钢板磁场变化量的大小，判断磁场稳定性的好坏。

冲击脉冲的持续时间为0.5 s，幅值为2 A，产生约2倍的地磁场，每块钢板在对应每种波形消磁后均做1次冲击，结果磁场在冲击下的变化量（数据已做归一化处理）分别如图5和图6所示。

由图可以看出，如果考虑测量误差，可以说每种波形消磁后的结果磁场的稳定性几乎没有差别。

3．3 结论

由以上的理论分析和实验，可以得出以下结论:

1）针对不同厚度的船体钢板，可以采用不同的通电时间和脉冲幅值进行消磁，钢板越薄，则通电时间可以越短，幅值可以越小。

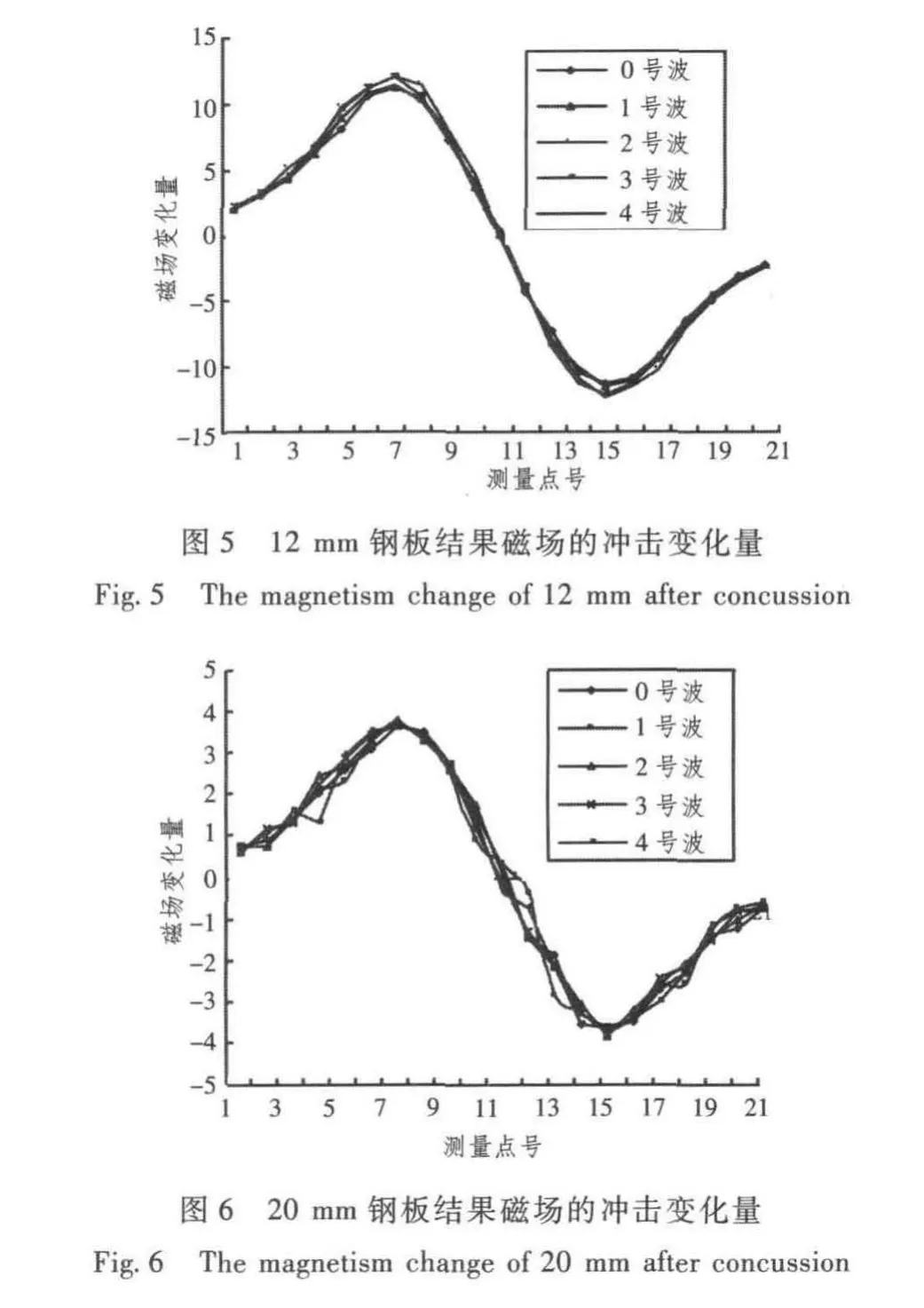
2）从理论上讲，过渡时间不同对磁化效果有一定的影响，但实验结果表明，它的影响微不足道，不是影响消磁效果和结果磁场稳定性的主要矛盾，主要因素是通电时间和幅值。

3）目前消磁工程中，对过渡过程指标的过高要求没有必要。在消磁电源能量足够的情况下，过渡过程相对延长，同样可以达到理想的消磁效果，这样可以降低对消磁电源设备和控制设备的要求，减小通断电时对供电机组的冲击，降低设计难度和造价。

4 结语

本文从消磁工程实际出发，首次提出了小阶跃叠加法，对实际消磁中应用的带有过渡过程的消磁电流对铁磁物质的磁化作用进行了建模和仿真，可以实时地计算出不同时刻不同深度的磁化效果，设计制作的可控电源系统实现了输出电流各种参数的可调，并实验验证了过渡过程不同的消磁电流的消磁效果和结果磁场稳定性的差别，得出的结论可以作为消磁电源系统设计的依据。

［1］张国友．舰船消磁原理及装置［M］．武汉:海军工程大学，2009，68－92．

ZHANGGuo-you．Elementandequipmentofship deguassing［M］．Wuhan:Naval University of Engineering．2009，68－92．

［2］钟顺时．电磁场基础［M］．北京:清华大学出版社，2006，46－50．

ZHONG Shun-shi．Elements of electromagnetic field［M］．Beijing:Publishing Company of Tsinghua 2006，46－50．

［3］肖昌汉．铁磁学［M］．北京:海潮出版社，1999．189－195．

XIAO Chang-han．Elementsofferromagneticmaterial［M］．Beijing:Publishing Company of Wave，1999．189－195．

［4］杨华军．数学物理方法与计算机仿真［M］．北京:电子工业出版社，2005．

YANG Hua-jun．Method of mathmatics and physics and computer simulation［M］．Beijing:Electron Indurstry Publishing Company，2005．

［5］王正明，刘明．精通MATLAB7［M］．北京:电子工业出版社，2006．WANG Zheng-ming，LIU Ming．Mastering of Matlab7［M］．Beijing:Electron Indurstry Publishing Company，2006.7．

［6］何汉林，梅家斌．数值分析［M］．北京:科学出版社，2007．

HE Han-lin，MEI Jia-bin．Analysis of data［M］．Beijing: Science Publishing Company，2007．

［7］BAYNES T M，RUSSELL G J，BAILEY A．Cmparison of stepwisedemagnetizationtechniques［J］．IEEE Transactions on Magnetics，2002，38（4）:1753－1758．

［8］MALCOLM T．Analysis of the demagnetization process and possible alternative magnetic treatments for naval vessels［D］．Sydney:The University of New South Wales，2002．