基于参考机的单机等面积暂态稳定分析＊

吴政球，周 野，匡文凯，刘堂伟

（湖南大学电气与信息工程学院，湖南长沙 410082）

基于参考机的单机等面积暂态稳定分析＊

吴政球†，周 野，匡文凯，刘堂伟

（湖南大学电气与信息工程学院，湖南长沙 410082）

提出了相对参考机的单机稳定裕度评估方法.研究了单一机组功角曲线的表达方式，将多机系统中单机功角曲线表达为本机相对参考机转子角度的函数，提出了基于泰勒级数的功角曲线预测拟合方法.提出了稳定裕度的预测评估方法与事后评估方法，比较了事后评估与预测评估所得稳定裕度的差异.SGEAC方法在判别系统是否稳定时没有任何假设，不需要进行动态二群的识别.实例验证了所提方法的有效性.

暂态分析；裕度预测；功角曲线拟合；单机等面积判据；泰勒级数

电力系统稳定分析在寻找电力系统稳定裕度和失稳机理方面取得了大量的研究成果.分析方法主要有暂态能量函数法［1－4］、数值仿真法［5－9］和二者相结合的混合法.能量函数法又包括基于PEBS与RUEP的能量函数法［10］、扩展等面积法（EEAC及SMEAC）［11－13］、单机等面积（SGEAC）［14］等方法.时域仿真的优点是能考虑任意复杂的系统模型，通过多次计算，可得到基于临界切除时间的稳定裕度，但不能快速得到反应系统暂态稳定裕度的能量型量化指标.对大系统而言，由于很难确定失稳模式及相关不稳定平衡点，基于RUEP的能量函数法使用起来不是很方便.基于最大势能搜索的势能边界法（PEBS）很难得到能量型稳定裕度量化指标.为了克服PEBS能量函数法的不准确性，在系统惯性中心的基础上采用了基于双机等值的修正动能，该修正动能修正掉了与二群各自内部各机组之间的“布朗运动”相对应的、对系统失稳没有影响的动能.EEAC及其改进方法［11－13］在同步坐标基础上定义了动态二群机组的等值角度与速度，并进一步定义了基于动态二群相对运动且能反应系统失稳裕度的加速面积与减速面积（动能与势能）.

文献［14］提出了多机系统的单机等面积法暂态稳定判据，效果很好，但没有对多机系统中单机功角曲线进行深入研究.

本文研究了多机系统中单一机组功角曲线的表达方式，提出了基于泰勒级数的功角曲线预测拟合方法，将多机系统中单机功角曲线表达为本机相对参考机转子角度的函数.提出了稳定裕度的预测评估方法与事后评估方法，比较了事后评估与预测评估所得稳定裕度的差异.基于SGEAC的单机等面积方法没有对电力系统动态模型作任何假设，不需要对失稳模式进行辨别，稳定判别结果与时域仿真完全一致.与时域仿真法相比较，利用单机等面积法可方便地求得基于能量的稳定与不稳定裕度.

通过对简单6机系统及IEEE 17机测试系统的分析，证实了本文所提方法的快速性、可靠性和有效性.

1 SGEAC思想的单机稳定裕度

机组转子运动方程为：

式中：ωi为转子角速度和同步速的偏差；为转子角度；Pm，i为机组的机械功率；g为发电机组总台数.

在系统后向机群中指定一台发电机r为参考机，其运动方程为：

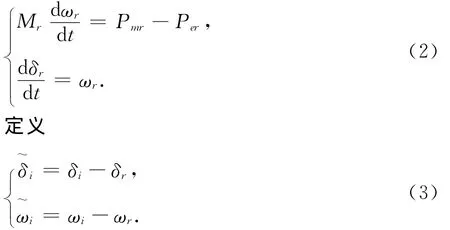
式中：ADec，i为发电机i的减速面积；AInc，i为发电机i的加速面积为发电机i相对参考机的不稳定平衡点角度为故障切除时发电机i相对参考机的角度；为故障切除时发电机i相对参考机的角速度；为发电机i相对参考机的平衡点功角；为发电机i相对参考机的平衡点角速度；为扰动结束后发电机i的功角曲线.若sηi＜0，则发电机i此摆失稳，此时系统将失去稳定；若sηi＞0，则发电机i此摆稳定.

根据拟合得到的曲线，解方程（10）可预测发电机i的不稳定平衡点功角.

显然，实际分析时，选取功角最小的机组作为参考机，对前向机群中功角最大机组进行稳定裕度计算就可判断系统的稳定性.

2 功角曲线拟合的理论基础

不管是采用EEAC方法、还是采用单机等面积方法进行稳定裕度的评估，都必须知道相应的功角曲线.根据EEAC理论，EEAC等值机功角曲线为拟合得到的正弦曲线.在动态二群的思路下，即使在基于参考机的单机情况下，如果系统能动态分为二群的话，其电磁功率也可表达为相对参考机的本机功角的正弦函数.系统动态过程中，正弦函数的参数会不断发生变化，这一点与动态EEAC的思路是一致的.为了获得当前功角点到不稳定平衡点˜δcri之间的尚未仿真得到的功角曲线，本文采用多项式拟合技术进行相对参考机的单一机组的功角曲线拟合，该方法不需要机组分群的假设.

由理论分析可知机组I的等效电磁功率可表达为：

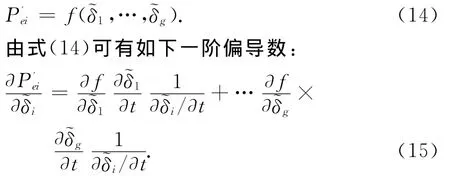
同理可计算出电磁功率对功角的高阶偏导数.

虽然多机系统中，任意发电机电磁功率看起来是所有发电机转子角度的函数，但实际上真正的独立变量只有一个，即时间.由式（15）及其高阶表达式可知：多机系统中任意单机电磁功率都可表达为本机相对参考机转子角度的多项式函数.

这种形势下，专业的人在西王做得了专业的事吗？对于大纪和大龙来说，他们是西王的“外人”，尤其是大纪，在集团和俱乐部来说属于“客人”，最终的话语权在西王老板及其老乡身上；大纪本身的性格特点，也决定了他不争不抢，对于西王方面的一些不合理的事情，估计大纪也难有勇气去抗争。

大量算例表明：机组在达到最大角度之前与之间是一条连续可微曲线.由泰勒级数有：

由数学分析可知，在展开点附近的一个邻域内，泰勒级数能较好地吻合原曲线.由当前功角点之前的时刻点上功角曲线数据拟合得到的功角曲线函数应该可以很好地预测当前功角点到不稳定平衡点之间的曲线.计算上述高阶导数很费机时，本文利用仿真得到的（）通过拟合得到的高阶泰勒级数来预测单一机组从当前功角点到不稳定平衡点之间的曲线.

3 算 例

本文算例采用事后评估与预测评估的方法来评估系统的稳定裕度.对于失稳情况，事后评估是根据仿真结果得到故障切除时刻或稳定平衡点时刻研究机组的角速度，以及研究机组在不稳定平衡点时刻的角速度，由式（11）计算稳定裕度.对于稳定情况，事后评估是根据仿真得到的基于参考机的研究机组到达最大功角之前的功角曲线数据拟合得到最大功角点到不稳定平衡点之间的功角曲线，利用本文提出的相关计算公式计算得到相应稳定裕度.所谓预测评估就是利用当前功角点之前0.1 s的功角曲线数据，利用拟合并外延得到相应功角曲线，能够在机组达到最大功角点或者不稳定平衡点之前并计算出相应机组的稳定裕度.

3.1 6机系统失稳故障的事后评估

在5号节点发生三相瞬时短路，0.38 s故障切除，摇摆曲线如图1所示.其中，1和6号机为前向机群，其余为后向机群.

图1 失稳摇摆曲线Fig.1 Swing curves for unstable case

选取2号机作为参考机，在故障切除时刻0.38 s时，1号机相对参考机的角速度为＝0.007 5，在0.63 s时，1号机相对参考机的临界角速度为＝0.004 4，由（11）式可以得到1号机相对参考机的稳定裕度为－0.344.同样，选取2号机作为参考机，在故障切除时刻0.38 s时，6号机相对参考机的角速度为＝0.009 8，6号机相对参考机的临界角速度为＝0.006 2，由（11）式可以得到6号机相对参考机的稳定裕度为－0.4.上述结果如表1所示，由表1数据可知，临界机群中最严重单机的稳定裕度与EEAC所得稳定裕度基本一致.另外，单机稳定裕度稳定判断得到的临界切除时间与EEAC稳定判断得到的临界切除时间完全一致.

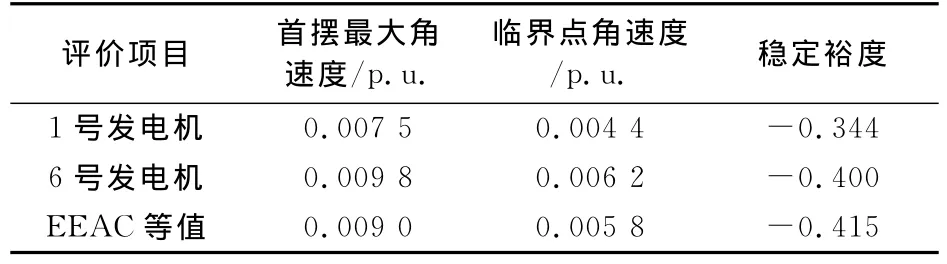
表1 事后评估的不稳定裕度指标Tab.1 Stability margins for unstable scenarios

3.2 6机失稳故障的预测评估

根据故障切除后短时间的仿真数据，样本时间为0.1 s，根据多项式拟合得到研究对象的功角曲线.在当前功角点时，由式（5）可以得到稳定裕度计算式（18）：

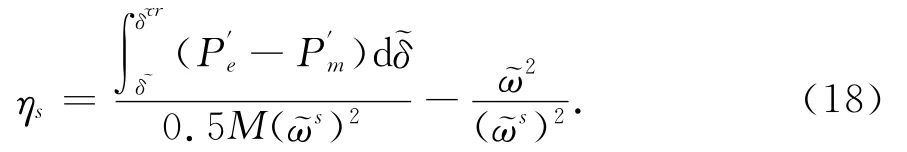
利用故障后0.1 s数据及式（18）计算得到稳定裕度如表2所示.由表中数据可知，不管是EEAC等值机群、还是相对参考机的单机，均能得到相似的稳定裕度；临界机群中最严重单机的稳定裕度与EEAC所得稳定裕度基本一致.

随着仿真时间的延长，拟合样本数据（样本时间窗口为0.1 s保持不变）的不断更新，表2中的单机等面积预测的裕度越来越接近表1所示的事后评估的裕度指标，因而预测评估可用于基于PMU测量的暂态稳定预测分析，可有效提前判别系统稳定性.

表2 基于功角曲线预测的稳定裕度Tab.2 Stability margins by using power angle curve prediction

3.3 6机系统稳定场景的分析

为了得到量化稳定裕度，一个关键问题是要得到相应功角曲线.当故障不是很严重且功角曲线没有越过最大电磁功率点时，不管是基于EEAC等值机、或者是单一机组，不同样本时刻拟合功角曲线得到的裕度指标有一些变化，但都能正确判断系统稳定.当相关功角曲线接近或越过最大电磁功率点时，拟合功角曲线得到的裕度指标比较稳定.

当15号节点发生三相短路，0.16 s故障切除时，系统摇摆曲线见图2.

图2 稳定的摇摆曲线Fig.2 Swing curves for unstable case

由图2可知，不同机组摇摆交织在一起.在2.76～2.85 s内，1，4，5和6机为前向机群，2和3机为后向机群，利用EEAC得到的稳定裕度为0.4.在2.85～2.95 s内，1，2，4，5和6机为前向机群，3机为后向机群，利用EEAC得到的稳定裕度为0.62.

利用基于参考机的单机等面积定则进行系统稳定判别时，不需要知道所有机组的稳定裕度，只需得到临界机群中的单机相对于参考机的稳定裕度就可判别系统稳定性.利用多项式拟合得到1号机在0.35，1.55及2.95 s附近的功角曲线如表3所示，计算得到其稳定裕度分别为3.65，2.38和0.28，可见单机等面积稳定裕度正确反应了机组的摇摆严重程度.

表3 稳定场景的稳定裕度指标Tab.3 Stability margins for stable scenarios

3.4 IEEE 17机标准测试系统分析结果

按照文献［15］中的数据，采用不同仿真数学模型对IEEE 17机标准测试系统进行了分析，结果令人满意.文中给出了发电机采用E′q恒定模型，负荷用恒定阻抗模型的数据分析结果.时域仿真时仿真步长为0.01 s.Bus3母线处的发电机作为参考机.

当系统故障为0 s 75母线处三相短路，0.356 s断开75母线至9母线之间的线路来切除故障时，在故障点附近的Bus6，Bus73，Bus76，Bus114和Bus130遭受巨大扰动，其中Bus130发电机在二摆失稳，故障切除后部分发电机的摇摆曲线如图3所示.

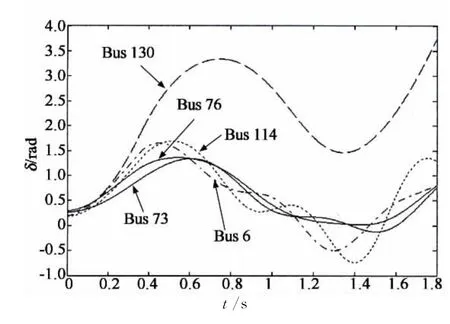
图3 0.356 s切除故障系统部分发电机摇摆曲线Fig.3 Generator swing curve for fault cleared at 0.356 seconds

采用故障后0.1 s内仿真得到的功角数据，由多项式功角曲线拟合得到相对参考机的单机功角函数，利用公式（18），得到故障1时暂态稳定裕度结果如表4所示.由表4可知，系统首摆裕度为0.432，裕度较小，需进一步监视.由单机越过二摆平衡点以后0.1 s的仿真数据进行拟合得到功角函数以后，得到相对参考机的单机稳定裕度如表5所示.由表5数据可知，除了失稳机组以外，其他机组的二摆稳定裕度较首摆裕度都有所增加，仿真得到的摇摆曲线中二摆最大角度均有所减小，因而，稳定裕度反映了机组的稳定情况.

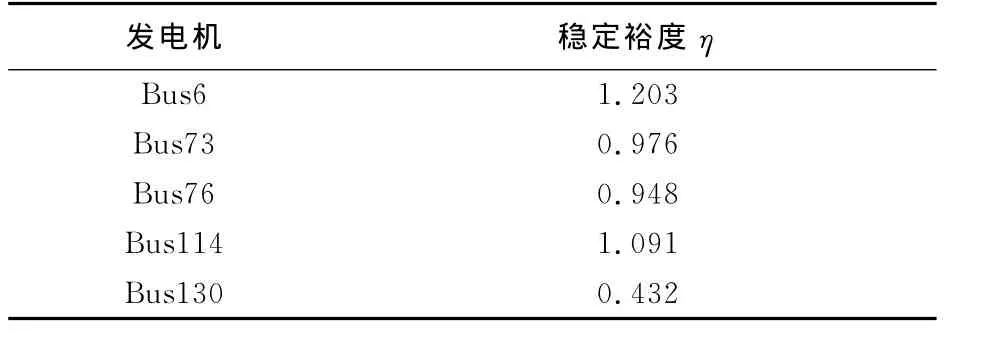
表4 首摆稳定裕度Tab.4 Stability margin for the first swing

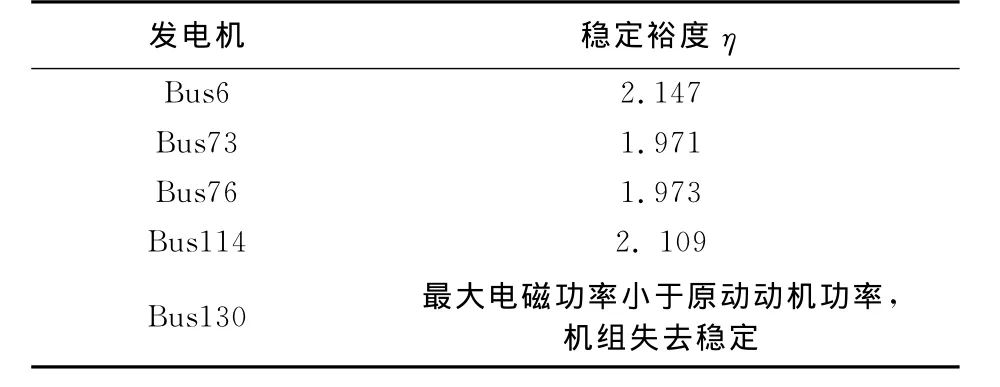
表5 第二摆稳定裕度Tab.5 Stability margin for the second swing

当系统在26母线处发生三相短路，0.194 s后切除（25～26）线路，系统摇摆曲线如图4所示.此时系统是二群失稳模式.本文方法得到73机在0.596 s时的稳定裕度为－0.732，系统将失去稳定，与仿真结果完全一致.应当注意的是，本文方法判别系统失去稳定的时间（0.596 s）要早于180度功角差的时间.

图4 0.196 s切除故障系统部分发电机摇摆曲线Fig.4 Generator swing curve for fault cleared at 0.196 seconds

应当指出的是：本文稳定分析是以参考机为基础进行的，参考机一般为后向机群中的临界机.因此本文方法只需对前向机群中的临界机进行分析就可判断系统的稳定性.

4 结 论

提出了相对参考机的单机稳定裕度评估方法、稳定裕度的预测评估方法与事后评估方法，由泰勒级数分析得出了多机系统中单一机组的功角曲线可由机组本身的转子角度来表示，得到了单机功角曲线的理论曲线.利用时域仿真结果，结合最小二乘法拟合出了单机多项式功角P-δ曲线.分析表明所提算法实用可行正确，具有较好的超前稳定判别能力，可有效减少时域仿真时间，预测方法精度高、计算速度快，不需要进行动态分群.

［1］ PHADKE A G.Synchronized phasor measurements in power systems［J］.IEEE CAP，1993，6（2）：10－15.

［2］ STEWART E S，CHARLIE S，KENNETH M，etal.Application of phasor of measurement and partial energy analysis in stabilizing large disturbances［J］.IEEE Transactions on Power Systems，1995，10（1）：297－306.

［3］ FOUAD A A，VITTAL V.Power system transient stability analysis using the transient energy function method［J］.Prentice Hall，1992，5（3）：23－29.

［4］ 吕志来，张保会，哈恒旭.基于改进的势能界面判据实时预测电力系统稳定性［J］.中国电机工程学报，2002，22（4）：94－99.

LV Zhi-lai，ZHANG Bao-hui，HA Heng-xu.Real time fast predict transient stability based corrected potential surface criterion［J］.Proceedings of the CSEE，2002，22（4）：94－99.（In Chinese）

［5］ 滕林，刘万顺，貟志皓，等.电力系统暂态稳定实时紧急控制的研究［J］.中国电机工程学报，2003，23（1）：64－69.

TENG Lin，LIU Wang-shun，YUN Zhi-hao，etal.Study of real-time power system transient stability emergency control［J］.Proceedings of the CSEE，2003，23（1）：64－69.（In Chinese）

［6］ 于继来，郭志忠，柳焯.基于能量型高阶Taylor级数展开技术的直接法［J］.电网技术，1995，19（2）：18－24.

YU Ji-lai，GUO Zhi-zhong，LIU Zuo.Direct method with high order taylor series expansions of energy function［J］.Power System Technology，1995，19（2）：18－24.（In Chinese）

［7］ 丁军策，蔡泽祥，王克英.基于广域测量系统的混合量测状态估计算法［J］.中国电机工程学报，2006，26（2）：58－63.

DING Jun-ce，CAI Ze-xiang，WANG Ke-ying.Mixed measurements state estimation based on WAMS［J］.Proceedings of the CSEE，2006，26（2）：58－63.（In Chinese）

［8］ MARIA G A，TANG C，KIM J.Hybrid transient stability analysis［J］.IEEE Transactions on Power Systems，1990，5（2）：384－391.

［9］ TANG C K，GRAHAM C E，EI-KADY M，etal.Transient stability index from conventional time domain simulation［J］.IEEE Transactions on Power Systems，1994，9（3）：1524－1530.

［10］江宁强，宋文忠，戴先中.基于稳定域边界的主导不稳定平衡点（BCU）法前提条件的验证［J］.中国电机工程学报，2004，24（6）：48－52.

JIANG Ning－qiang，SONG Wen-zhong，DAI Xian-zhong.A restriction on the power system by theoretical requisitions of the BCU method［J］.Proceedings of the CSEE，2004，（6）：48－52.（In Chinese）

［11］薛禹胜.EEAC和FASTEST［J］.电力系统自动化，1998，22（9）：25－30.

XUE Yu-sheng.EEAC and FASTEST［J］.Automation of Power Systems，1998，22（9）：25－30.（In Chinese）

［12］BETTOIL A L，WEHENKEL L，PAVELLA M L.Transient stability constrained maximum allowable transfer［J］.IEEE Transactions on Power System，1999，14（2）：654－659.

［13］ERNST D，RUIZ＿VEGA D，PARVELLA M，etal.A unified approach to transient stability contingency filtering，ranking and assessment［J］.IEEE Transactions on Power Systems，2001，16（3）：435－443.

［14］吴政球，陈辉华，唐外文，等.以单机等面积稳定判据分析多机系统暂态稳定性［J］.中国电机工程学报，2003，23（4）：48－52.

WU Zheng－qiu，CHEN Hui-hua，TANG Wai-wen，etal.U-sing single machine equal area criterion to analyze multi-machine systems stability［J］.Proceedings of CSEE，2003，23（4）：48－52.（In Chinese）

［15］VITTAL V.Transient stability test systems for direct stability methods［J］.IEEE Transactions on Power Systems，1992，7（1）：37－43.

A Fast Quantitative Transient Stability Margin Determination Method Based on SGEAC

WU Zheng－qiu†，ZHOU Ye，KUAN Wen-kai，LIU Tan-wei
（College of Electrical and Information Engineering，Hunan Univ，Changsha，Hunan 410082，China）

Based on single machine equal area criterion，the stability margin based on single study generator and reference generator was defined.The power angle curve expression for single study machine was analyzed.Based on the Taylor series，the power angle curve of single study generator can be expressed as the function of the rotor angle of the study generator with respect to the reference machine angle，which is fitted by using polynomial function.The stability margins obtained by both prediction method and post event method were compared.Single Generator Equal Area Criterion（SGEAC）based stability margin is the real evaluation of the global stability margin，and it does not need the identification of the two group mode.Lots of example analysis verified the proposed method.

transient analysis；margin prediction；power angle curve prediction；single machine stability margin；Taylor series

TM731

A

1674-2974（2011）06-0049-06＊

2010-06-15

湖南省科技厅重大专项资助项目（2008FJ2003）

吴政球（1963－），男，湖南岳阳人，湖南大学教授，博士生导师

†通讯联系人，E-mail：zhengqiuwu＠163.com