基于格的代理签名方案＊

夏 峰，杨 波，马 莎，孙微微，张明武

（1.华南农业大学信息学院，广东广州 510642；2.海南师范大学信息科学技术学院，海南海口 571158）

基于格的代理签名方案＊

夏 峰1，2，杨 波1†，马 莎1，孙微微1，张明武1

（1.华南农业大学信息学院，广东广州 510642；2.海南师范大学信息科学技术学院，海南海口 571158）

利用原像采样单向陷门函数和盆景树下格的扩展及格基的随机化方法，基于格构造了一个代理签名方案.在随机预言机下，基于平均情况的小整数解问题SIS（Small Integer Solution）和非均匀小整数解问题ISIS（Inhomogeneous Small Integer Solution）的困难性假设，证明该方案在适应性选择消息攻击下是安全的.与基于数论假设方案相比，该方案密钥空间较大，但计算效率更高.

格；随机预言机；代理签名；原像采样

为高效、安全地实现数字签名的委托，1996年，Mambo等［1］提出了代理签名的概念.此后，代理签名体制得到了广泛、深入的研究，出现了许多基于大整数分解和离散对数问题的代理签名方案，并且，这种签名机制已被广泛地应用到网格计算、电子交易、移动通信和移动代理等环境.然而，若量子计算机得到应用，基于数论假设的大整数分解问题和离散对数问题都可在多项式时间内得到解决［2］，大量基于数论假设的代理签名方案将不再安全.因此，设计能抵抗量子攻击的代理签名方案成为该领域需解决的问题.近年来，基于格构造新型密码系统因具有较高的渐近效率、运算简单（通常只需要线性运算）、能抵抗量子攻击和存在最坏情况下的随机实例等特点，成为公钥密码领域的研究热点，并取得了一系列的研究成果［3－7］.本文基于格中平均情况下SIS和ISIS问题的困难性假设，利用带原像采样的单向陷门函数和盆景树下格的扩展及格基的随机化方法，基于格构造了一个高效、安全的代理签名方案.

1 预备知识

1.1 符号说明

1.2 格上的困难问题

1.3 格上的高斯分布

对于任意s＞0，定义以向量c为中心，参数为s的高斯分布为：

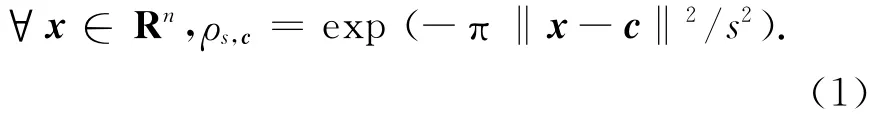
格上的离散高斯分布为：

式（1），式（2）中，若s，c分别是1和0，在书写时则可省略.离散高斯分布是一个条件分布函数，是由对格中的元素按高斯分布取样所获得的分布.

高斯分布格点范围的大小主要由s来决定，当s的取值满足一定条件时，则在离散高斯分布中采样输出格点的分布及长度会有一些比较好的性质，下面的定义给出与s相关的平滑参数的定义.

定义5［9］平滑参数（The smoothing parameter）.设任意一个n维格Λ和ε＞0，定义平滑参数ηε（Λ）为最小的s＞0，使得ρ1／s（Λ＊＼｛0｝）≤ε.

当s≥ηε（Λ）时，定理2给出了对离散高斯分布中的向量进行采样时获得向量概率的最大上界.

定理2［3］对于任意秩为k的n维格Λ，c∈Rn，正数ε＜exp（－4π）和s≥ηε（Λ），对每一个x∈Λ有：

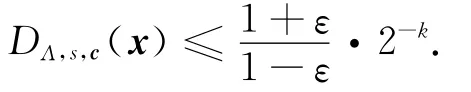
特别地，DΛ，s，c（x）的最小熵为k－1.

1.4 采样算法和原像采样单向陷门函数

文献［3］给出了运行时间约为格基长度的O（n2）的采样算法SampleD（B，s，c），通过该采样算法获得的向量满足下面的定理.和，则以压倒性的概率，u＝Aemodq在

定理4描述若以格的离散高斯分布上采样所得的格点作为输入，则其与随机均匀选取的矩阵向量积在该矩阵所生成的向量空间上也是均匀分布的.

定理4［3］设n和q为正整数且q为素数，令m≥2nlgq，对于所有的时，基于平均情况问题SIS和I-SIS的单向陷门函数，简单描述如下［3］：

1）按定理5生成（A，S）.其中，A为公钥，S为私钥.

2）函数fA定义为fA（e）＝Ae（modq），定义域为上是统计均匀分布的.

基于平均情况问题SIS和ISIS，文献［3］构造了一个单向陷门函数，在描述该函数之前，我们给出下面定理.

定理5［10］给定任意素数q＝poly（n）和任意m≥5nlgq，存在一个概率多项式算法，输入1n，输出矩阵A∈Zn×mq和一个满秩的集合S⊂Λ⊥（A，q），A在Zn×mq上是统计均匀分布的，并且‖S‖≤L＝m2.5.

在文献［3］中，Gentry等人将L优化到m1＋ε.，值域为Rn＝Znq.e的输入分布满足DZm，s.

3）单向陷门求逆算法SampleISIS（A，S，s，u）求得f－1A（u）如下：先计算t∈Zm，然后利用高斯采样算法用私钥S采样出v←DΛ⊥，s，－t，输出e＝v＋t.e即为u在给定定义域的原像.

定理6［3］算法SampleISIS（A，S，s，u）若是单向的，则平均情况是困难的.而且若fA（e）＝Ae（modq）是抗原像采样碰撞攻击的，则平均情况是困难的.

1.5 格的扩展和格基的随机化操作

在2010年的欧密会上，David Cash等［11］把盆景树的思想引入到格中，给出了对格进行扩展（使其秩增加）和对基进行随机化操作的具体方法.下面给出本文中要用到的有关定理和定义.

定理7［12］每一个格Λ⊆Zm都可用埃尔米特插值标准形式（Hermite normal form）唯一地表示出来，它可用给定格的任意基B高效地计算出来，写成HNF（B）.

定理10说明了SR和S相互独立，即由SR得不到任何S的特定信息，通过该定理，可有效地实现格基的委托，即把原来的基随机化之后，得到新的基，且从新的基无法推导出原来的基.该定理主要用到定理7和定理8的结果.

2 基于格的代理签名方案

2.1 方案描述

定义6 基于格的代理签名方案（LatticeProSig）包括系统密钥生成（SigKeyGen）、代理密钥生成（ProSigkeyGen）、代理签名（ProSig）和签名验证（Ver）4个算法，具体描述如下.

2.2 安全性证明

对该定理的证明分为3个部分：首先证明代理密钥不泄露原始签名者私钥的任何信息，而且，不知道原始签名者私钥，任何人无法伪造代理密钥；其次证明任何不知道代理密钥的第3方无法伪造代理签名；最后证明不知道代理签名的私钥者无法冒充该代理人伪造代理签名.

证 先证明第1部分：在用算法RandBasis（S‴，s）生成Sδ时，根据定理10，这是一个随机化的操作，生成的Sδ与S‴相互独立，从Sδ得不到任何关于S‴的特定信息，从而，无法从Sδ求出S‴，进一步，也无法求出S′.相反，因为A′和都是均匀随机选取的，所以A′‖也是均匀随机的，在给定A′‖时，假设一个敌手在不知道原始签名者的私钥S′时，能伪造代理密钥Sδ，则他可通过采样算法SampleD（S，sδ，0）获取eδ，使得（A′‖）eδ＝0（modq），这样，他就解决了在下的平均情况SI问题，这与定理1矛盾.因此，在不知道原始签名者的私钥时，敌手无法伪造代理密钥.第1部分得证.

第2部分是证明H（M）＝（A′‖）eδ的安全性，我们将基于随机预言机模型证明它能抗击适应性选择消息攻击.证明方法与文献［3］提出的证明方法类似，证明如下：

假设存在一个敌手AI能伪造代理签名，则存在一个多项式时间算法SI能找到关于H（·）的一对碰撞.

H（·）询问：对AI每一个不同的M∈｛0，1｝＊，SI先查找本地存储是否有（M，eδ），若有，则返回H（M）＝（A‖）eδ，否则用采样算法SampleD（S，sδ，0）随机获取eδ，计算H（M）＝（A‖A¯）eδ，并将其返回给AI，并保留（M，eδ）.

签名询问：当AI询问M的签名时，SI查表（M，eδ），并将eδ做为M的签名返回给AI.

最终，AI将伪造出一对有效的签名（M＊，eM），因为AI在伪造签名时必须要对M＊进行H（·）询问，从而，SI在本地保留（M＊），根据定理4，eδ←SampleD（S，sδ，0）有均匀输出的特性，根据定理2，在随机均匀地给定H（·）的情况下，发生的概率最大值为），对于足够大的m＋m¯和足够小的的概率可以忽略，所以有.从而，SI找到了，使得（A，即找到，使得，这与是困难的相矛盾.第2部分得证.

第3部分是证明u＝A″e′的安全性.这部分证明与第2部分证明类似，在这里不做详细描述.

证毕.

若同一个原始签名者要选择多个代理人，可选择不同的A¯（列数相同），并分别生成不同的代理密钥，定理12说明这并不影响代理签名的安全性.

定理12 同一个原始签名人的不同代理者无法从自己的代理密钥推导出其他代理者的密钥.

证毕.

由以上证明可知，完全可将代理者信息用杂凑函数计算后陷入到中而并不影响签名的安全性.

2.3 效率分析

该代理签名方案的效率主要取决于代理签名和签名验证部分的效率，密钥的长度约为O（n2），采样算法所需运行的时间约为输入参数长度的O（n2），验证eδ，e′范围所需的时间为O（n）.此外，还需要做2个杂凑函数的运算和2个向量的线性运算即可.在效率上，与基于数论的代理签名方案相比，其缺点是密钥长度比效大，但不需要模指数运算，其计算效率显然更高.

3 结束语

基于格的密码体制在最近几年有了较快的发展，构造基于格的签名体制主要依赖于平均情况SIS问题的困难性假设，而盆景树下格的扩展和格基的随机化方法在构造具有某些特殊属性的签名体制方面有着重要的应用.本文利用带原像采样的单向陷门函数和盆景树下格的扩展和格基的随机化方法，构建了一个基于格的代理签名方案，并基于随机预言模型，证明该方案在选择消息攻击下是可证安全的.与传统的基于数论的代理签名方案相比，该方案的密钥空间较大，但运算简单（只需线性运算），能抵抗量子攻击.

［1］ MAMBO M，USUDA K，OKAMOTO E.Proxy signatures for delegating signing operation［C］／／Proc 3rd ACM Conference on Computer and Communications Security.New York：ACM，1996：48－57.

［2］ SHOR P W.Polynomial-time algorithm for prime factorization and discrete logarithm on a quantum computer［J］.SIAM Journal on Computing，1997，26（5）：1484－1509.

［3］ GENTRY C，PEIKERT C，VAIKUNTANATHAN V.Trapdoors for hard lattices and new cryptographic constructions［C］／／Proc 40th ACM Symp on Theory of Computing（STOC）.New York：ACM，2008：197－206.

［4］ REGEV O.On lattices，learning with errors，random linear codes，and cryptography［J］.Journal of the ACM，2009，56（6）：1－40.

［5］ PEIKERT C.Public-key cryptosystems from the worst-case shortest vector problem［C］／／Proc 41st ACM Symp on Theory of Computing（STOC）.New York：ACM，2009：333－342.

［6］ AGRAWAL S，BONEH D，BOYEN X.Efficient lattice（H）IBE in the standard model［C］／／Advances in Cryptology-Eurocrypt 2010.Berlin：Springer Verlag，2010：553－572.

［7］ LYUBASHEVSKY V，PEIKERT C，REGEV O.On ideal lattices and learning with errors over rings［C］／／Advances in Cryptology-Eurocrypt 2010.Berlin：Springer Verlag，2010：1－23.

［8］ LENSTRA A K，LENSTRA H W，LOV′ASZ L.Factoring polynomials with rational coefficients［J］.Math Ann，1982，261（4）：515－534.

［9］ MICCIANCIO D，REGEV O.Worst-case to average-case reductions based on gaussian measures［J］.SIAM J Comput，2007，37（1）：267－302.

［10］AITAI M.Generating hard instances of the short basis problem［C］／／ICALP 1999.Berlin：Springer Verlag，1999：1－9.

［11］CASH D，HOFHEINZ D，KILTZ E，etal.Bonsai trees，or how to delegate a lattice basis［C］／／Advances in Cryptology－EUROCRYPT 2010.Berlin：Springer Verlag，2010：523－552.

［12］MICCIANCIO D，WARINSCHI B.A linear space algorithm for computing the Hermite normal form［C］／／Proceedings of the 2001 International Symposium on Symbolic and Algebraic Computation（ISSAC）.Berlin：Springer Verlag，2001：231－236.

Lattice-based Proxy Signature Scheme

XIA Feng1，2，YANG Bo1†，MA Sha1，SUN Wei-wei1，ZHANG Ming-wu1

（1.College of Informatics，South China Agricultural Univ，Guangzhou，Guangdong 510642，China；2.School of Information Science and Technology，Hainan Normal Univ，Haikou，Hainan 571158，China）

By using trapdoor functions with preimage sampling，lattice＇s growth，and lattice basis randomization in the bonsai tree，a lattice-based proxy signature scheme was proposed.The security of the proxy signature is based on the hardness of average-case SIS（Small Integer Solution）and ISIS（Inhomogeneous Small Integer Solution）.It is also existential unforgeability under adaptive chosen-message attack in the random oracle.Compared with the schemes based on factoring or discrete log，the public and secret keys of our scheme are larger，but it requires only linear operation on small integers.

lattice；random oracle；proxy signature；preimage sampling

TP309

A

1674-2974（2011）06-0084-05＊

2010-12-01

国家自然科学基金资助项目（60973134）；广东省自然科学基金资助项目（10351806001000000）

夏 峰（1975－），男，湖南永州人，华南农业大学博士研究生

†通讯联系人，E-mail：byang＠scau.edu.cn