驱动场下二组份BEC原子的量子动力学

刘志荣

（华东交通大学基础科学学院，江西 南昌 330013）

1924年印度科学家玻色（Bose）将光子作为数量不守恒的粒子成功地导出了普朗克黑体辐射定律。爱因斯坦（Einstein）将其推广到全同粒子理想气体，并从理论上预言了玻色-爱因斯坦凝聚现象的存在即在很低的温度下无相互作用的玻色子会在最低能量量子态上突然凝聚达到可观的数量。玻色-爱因斯坦凝聚体具有奇特性质，通过对它的研究可以发现原子间的相互作用力、外场等对物质凝聚过程及动力学的影响，这不仅对基础研究有重要意义，而且在原子激光、原子钟、原子芯片技术、精密测量、量子计算机和纳米技术等领域也有很好的应用前景。早期由于找不到合适的实验体系以及受当时实验技术的限制，玻色-爱因斯坦凝聚的早期实验研究进展十分缓慢。1995年7月美国科罗拉多大学实验天体物理联合研究所（JI⁃LA）Wiema小组[1]首先在实验中观察到了87Rb原子的玻色-爱因斯坦凝聚现象。同年美国的另两个小组分别在锂（7Li）[2]和钠（23Na）[3]原子蒸汽中实现了原子BEC。2001年度诺贝尔物理学奖分别授予了Eric A.Cor⁃nell，Wolfgang Ketterle及Carl E.Wieman，以表彰他们在实现弱相互作用玻色气体的玻色-爱因斯坦凝聚实验方面的开创性工作。2004年国际著名学术刊物《科学》将实现费米子的玻色-爱因斯坦凝聚评为年度国际科技十大进展之一。当前玻色-爱因斯坦凝聚的理论和实验研究已成为国际物理学界的研究热点之一。

2001年D.S.Hall等[4]对BEC的实验研究发现，外场下二组份BEC中第二组份原子数密度的演化呈现周期性振荡。中国科学院物理研究所李卫东研究员等[5]的理论研究结果与文献报导的实验结果符合。文献[5]还研究了二组份BEC的干涉等特性并得到了一些有趣的结果。本文研究驱动场作用下二组份BEC原子数密度的长时演化规律，深入研究驱动场Rabi频率、驱动场与原子的耦合强度及系统BEC二组份原子初始相对位相差对原子数密度演化特性的影响规律。结果表明：长时间的动力学行为表现出与短时间动力学行为不同的结果，即长时间范围内原子数密度演化呈现出量子体系特有的崩塌-复苏现象，且在较大的参数范围内，体系的崩塌-复苏特性不会改变。

1 物理模型

考虑一个零温度下的二组份BEC系统，该系统的原子间具有弱的非线性相互作用及耦合驱动。实验中驱动耦合可由一短的双光子脉冲把原子从一个自旋态转变成另一个自旋态，即通过双光子拉曼过程得到[6]。二次量子化后，该系统的哈密顿量可写成

它们分别描述各组份内原子的相互作用、耦合驱动及不同组份间的原子的相互作用。式中φ1（）x为Gross-Pitaevskii方程的稳态解。

为了获得哈密顿量（5）式的解析本征态，引入以下玻戈留玻夫变换[5]

2 计算结果与分析

2.1 驱动场Rabi频率对原子数密度演化特性的影响

图1给出了原子数密度N2（t）随时间及驱动场Rabi频率的演化图，基本参数如下：q=1，g=0.49，χ=0.5，φ=π/6，ωrf=0.001，t=1.2，Ω=20～50。由图1（a）可见，在较短时间范围内原子数密度随着时间的演化呈现出近似周期性振荡，并似一余弦函数。同时可以看到，驱动场Rabi频率的大小对原子数密度振荡的周期的影响显著：随着Rabi频率的增大原子数密度演化周期将减小。

现将演化时间延长以考查原子数密度的长时间演化行为。从图1（b）可以看到原子数密度的长时间演化中呈现出量子力学中典型的崩塌-复苏现象。这与短时间的演化行为中Rabi频率显著影响原子数密度振荡的周期不同，长时间动力学行为中呈现的崩塌-复苏的周期并不受Rabi频率的显著影响。

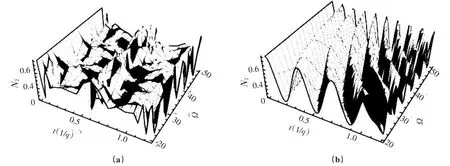
图1原子数密度N2（t）随时间及驱动场Rabi频率的演化关系图Fig.1The time evolution of the atomicity density N2（t）

2.2 驱动场耦合场强对原子数密度演化特性的影响

现研究驱动场耦合强度g的变化对原子数密度演化特性的影响，参数如下：q=1，χ=0.5，φ=π/6，ωrf=0.001，t=1.2，Ω=20，g=0～1.0。从图2（a）可以看到，短时间内原子数密度随时间演化呈现出周期性变化，且随着g的增大振荡的周期减小。特别当g为0时，原子数密度振荡周期为无穷大，即原子数密度维持在某一特定值不变。

在长时间的演化中，从图2（b）可以看到不论驱动场与原子的耦合是弱是强，原子数密度的演化均呈现出典型的崩塌-复苏现象，且崩塌-复苏的周期并不随耦合强度g的变化而显著变化。

图2原子数密度N2（t）随时间及驱动耦合场强度的演化关系图Fig.2The time evolution of the atomicity density N2（t）

2.3 二组份初始相对位相差对原子数密度演化特性的影响

从图3（a）可见（其中q=1，χ=0.5，ωrf=0.001，t=1.2，Ω=20，g=0～1.0，φ=0～4π），短时间内二组份初始相对位相差周期性地改变原子数密度的演化。位相差在kπ～kπ+1/2π（k为整数）范围振荡的幅度单调递增，而相差在（k+1/2） π～（k+1） π范围振荡的幅度单调递减。更有趣的是当φ=kπ时，原子数密度不随时间改变而维持在某一固定值不变。

从图3（b）可见，长时间内体系呈现的崩塌-复苏的幅度的变化规律与短时间振荡变化规律相似。

图3原子数密度N2（t）随时间及二组份初始相对位相的演化关系图Fig.3The time evolution of the atomicity density N2（t）

3 总结

本文研究了二组份BEC原子数密度的时间演化规律，研究结果表明原子数密度的长时间的演化特性与短时间演化特性不同，长时间范围内原子数密度演化呈现量子体系特有的崩塌-复苏现象。由于崩塌-复苏现象是量子体系特有的现象，它完全取决于体系的量子特性，系统崩塌-复苏性质不显受外场的影响。故在一定参数范围内原子数密度的演化呈现崩塌-复苏的特性不变。另本文详细讨论了驱动场Rabi频率、驱动场与原子的耦合强度以及BEC二组份初始相对位相差对原子数密度演化特性的影响规律。

[1]ANDERSON M H，ENSHER J R，MATTHEWS MR ，et al.Observation of Bose-Einstein condensation in a dilute atomic vapor[J].Science，1995，269（14）：198-201.

[2]DAVIS K B，MEWES M O，ANDREWS M R，et al.Bose-Einstein condensation in a gas of sodium atoms[J].Phys Rev Lett，1995，75（22）：3969-3973.

[3]BRANDLEY C C，SACKETT C A，TOLLETT J J，et al.Evidence of Bose-Einstein condensation in an atomic gas with attractive interactions[J].Phys Rev Lett，1995，75（9）：1687-1690.

[4]HALL D S，MATTHEWS M R，WIEMAN C E，et al.Measurements of relative phase in two-component Bose-Einstein condensates[J].Phys Rev Lett，1998，81（8）：1543-1546.

[5]LI W D，ZHOU X J，WANG Y Q，et al.Time evolution of the relative phase in two-component Bose-Einstein condensates with a coupling drive[J].Phys RevA，2001，64（1）：5602-5605.

[6]MATTHEWS M R，HALL D S，JIN D S，et al.Dynamical response of a Bose-Einstein condensate to a discontinuous change in internal state[J].Phys Rev Lett，1998，81（2）：243-247.

[7]KUANG L M，TONG Z Y，OUYANG Z W，et al.Decoherence in two Bose-Einstein condensates[J].Phys Rev A，2000，61（1）：3608-3613.

[8]CIRAC J I，LEWENSTEIN M，MOLMER K，et al.Quantum superposition states of Bose-Einstein condensates[J].Phys Rev A，1998，57（2）：1208-1218.

[9]MILBURN G J，CORNEY J，WRIGHT E M，et al，Quantum dynamics of an atomic Bose-Einstein condensate in a double-well potential[J].Phys RevA，1997，55（6）：4318-4324.

[10]WRIGHT E M，WONG T，COLLETT M J，et al.Collapses and revivals in the interference between two Bose-Einstein condensates formed in small atomic samples[J].Phys RevA，1997，56（1）：591-602.

[11]STEEL M J，WALLS D F.Pumping two dilute-gas Bose-Einstein condensates with Raman light scattering[J].Phys Rev A，1998，57（5）：3805-3808.

[6]胡红亮.图Cn及其r-冠的新的优美标号[J].纯粹数学与应用数学，2010，26（3）：454-457.

[7] 吴跃生，李咏秋.关于圈Cn的（r1，r2，…，rn）-冠（n=7，8）的优美性[J].阜阳师范学院学报：自然科学版，2010，27（3）：20-23.