基于组合滤波算法IP电话的回声消除
2011-03-06吴检波陈忠辉徐艺文魏宏安
吴检波,陈忠辉,徐艺文,魏宏安,陈 新
(福州大学 物理与信息工程学院,福建 福州 350108)
0 引言
近年来,随着网速的提高以及通信费用的降低,IP电话成为因特网上实现实时传送语音信号的一种新型通信业务,同时也成为计算机技术和通信技术研究的热点。IP电话之所以成为现代技术研究的热点,主要原因是 IP电话的网络带宽利用率高、通话成本低、灵活地提供丰富的增值功能而备受市场的关注。然而,IP电话与传统电话相比,由于其回声的影响,IP电话在因特网上进行语音的传输质量较差;因此,要提高IP电话话音质量,就必须对IP电话进行回声消除。为了消除 IP电话的回声,常用的自适应滤波算法有:最小均方误差算法(LMS,Least Mean Square)、能量归一化LMS算法(NLMS,Normalized LMS)、递归最小二乘算法(RLS,Recursive Least Square)、频域LMS算法(FLMS,Frequence LMS)等,但是这些算法都存在一些收敛速度、稳定失调的问题。综合各种算法的收敛性能和稳态性能,提出了一种组合比例算法,使其在快速收敛的情况下,具有较好的稳态性能。
1 相关算法
回声消除常用的自适应滤波算法有:LMS算法、NLMS算法、RLS算法、FLMS算法;LMS算法最简单,计算量最小,但收敛速度较慢,滤波器阶数过高时,容易造成误差积累,导致算法发散;NLMS算法是归一化的LMS算法,是自适应信号处理中应用最广泛的算法之一;它简单易实现,计算量适中,性能优于LMS算法,但收敛速度慢,对非平稳信号自适应能力差;RLS算法收敛性较好,但运算量正比于滤波器阶数的平方,IP电话中的回声信号延时达到几十毫秒,甚至更长,这就要求滤波器阶数较高,运算量也较大,稳态性能不好;FLMS算法是在频域内计算的一种方法,由于噪声抑制一般在频域内进行,如果回声抵消采用 FLMS算法,那么对噪声也会有一定的滤波作用,但计算量很大,且收敛速度慢。基于以上分析,提出一种组合比例自适应滤波算法,所选的组合算法在收敛性和稳态性方面必须具有一定的互补特性。
1.1 LMS算法
标准LMS算法是由其创始人Widrow和Hoff提出来的,该算法是线性自适应滤波算法。算法包括两个基本过程:滤波过程(filtering process)和自适应过程(adaptive process)。这两个过程一起工作组成一个反馈环,如图1所示,首先,围绕横向滤波器构造LMS算法,作用是完成滤波过程;其次,“自适应控制算法”部分对横向滤波器抽头权值进行自适应控制过程[1]。自适应滤波器控制原理是用误差序列e(n)按照误差的均方值最小化准则和算法对其系数w(n)进行调节,最终使自适应滤波的目标(代价)函数最小化,达到最佳滤波状态。LMS算法的基本思想是用平方误差来代替均方误差[2]。

图1 自适应滤波器框
标准LMS算法的运算步骤如下:
①初始化设置抽头输入向量u(n)(n=1,2,…,N -1)为任意值(一般均值为零),然后对每一次采样作以下各步的循环运算;
②计算经过滤波器的抽头权向量wH(n)输出;

③计算估计误差:

其中,d(n)为期望响应;
④更新N个滤波器权重系数:

其中µ为步长因子,是控制稳定性和收敛速度的参数;
⑤循环返回到②。
1.2 RLS算法
[3]。递归最小二乘算法旨在使期望信号与模型滤波器输出之差的平方和达到最小。当每次迭代中接收到输入信号的新采样值时,可以采用递归形式求解最小二乘问题,得到递归最小二乘算法(RLS)。该算法的目的在于选择自适应滤波器的系数,使观测期间的输出信号y(n)与期望信号在最小二乘的意义上最匹配。
①算法初始化


②对每一时刻,n=1,2,…计算增益矢量:

2 组合比例自适应滤波算法
组合比例自适应滤波算法是由LMS算法和RLS算法按照一定的比例组成,一方面可以解决收敛速度和稳态失调的矛盾,另一方面可以解决一种算法很难在多个性能指标上表现都好的问题。此算法的做法是,选择两种算法进行组合,同一时刻不同算法调整不同参数来达到最优组合,用误差能量最小的方法来调节组合比例系数得到一种性能好的算法。该算法只带来了计算量比较大的问题。但是,目前芯片技术的发展已大大提高了芯片的运算速度,这为该算法的运行提供了基础,因此运算量已不成问题。所以,将LMS和RLS两种算法按照一定的比例组合起来,形成组合比例自适应滤波算法(CP-RLSM,Combinate Proportionate RLS And LMS)。
组合比例自适应算法框图如图2所示。首先分别计算出LMS和RLS算法的误差,然后计算每一帧的误差能量,将LMS和RLS算法得到的能量误差进行分析,调整LMS和RLS相乘的参数λ(n)和1−λ(n)的比例得到一种算法,使得 CP-RLSM算法误差比这LMS和RLS算法都小。最后,将最小帧误差能量的误差作为输出。

图2 组合比例自适应算法框
组合比例自适应算法描述如下:

y1(n)和y2(n)分别是两个滤波器在n时刻的输出,yi(n)=(n) u(n),i=1,2,(n)和u(n)组成权向量滤波器,λ(n)是通过定义一个函数a(n)来限制范围为[0,1],函数a(n)和λ(n)对应的函数关系式为:λ(n)=sg m[a(n)]=。独立的滤波器w(n)和w(n)根据参数λ(n)组合得12到最优性能滤波器。

根据最速下降算法的定义可知 a(n+1)=a(n)-µa∇n从而可得a(n)变形的更新式如下:

式中µa为调整步长的参数,它的量纲为信号功率的倒数。
3 算法的仿真和分析
3.1 测试条件和方法
为了测试新算法的性能,使用采样频率为8 kHz正弦信号叠加零均值高斯加性白噪声来模拟语音信号。将信号通过自回归(AR,Autoregressive)滤波器产生的延迟信号来模拟通过听筒到麦克风而产生的回声信号。考虑到实际的实验环境和现有的实验条件,利用 MATLAB进行仿真,选择抽头数为9,步长为0.09的自适应滤波器来测试算法的性能,主要对算法的收敛性和稳态性进行分析。而这两项也正是自适应滤波算法应用于实际回声消除器时的主要指标。
3.2 自适应算法的性能分析


其中d(n)是期望信号,e(n)是误差信号。图3为MSE性能曲线,图4为误差性能曲线。从两图可以看出,经过自适应滤波以后,均方误差己经达到了10-30数量级以下,这相对于激励信号的幅度来说,基本可以忽略。回声衰减达到30 dB以上,因此,证实该算法的性能是比较优越的。图5为误差信号的输出曲线。可以看出误差曲线的幅度越来越小,说明回声消除起到了很好的效果。
从图3可以很清楚的看出,LMS算法以及RLS算法的收敛速率同CP-RLSM算法的收敛速率是无法比拟的,LMS和RLS算法要经过200多次迭代运算才会收敛,而CP-RLSM算法只需要几十次就己经收敛了。但是这并不能说明CP-RLSM算法比LMS和RLS算法在任何情况下收敛性都优越,因为实验仿真中在系统上并未做很苛刻的限制。此外,仿真中使用MATLAB的tic和toc命令[4]来测算程序运行的时间,时间越长代表对系统资源的消耗越多。三种算法中CP-RLSM算法用时最长,是RLS算法用时的一倍,是LMS算法用时的二倍。根据图5可以得出,在误差上CP-RLSM算法比LMS算法和RLS算法都优越。

图3 LMS、RLS、CP-RLSM算法均方误差

图4 LMS、RLS、CP-RLSM算法回声衰减增益
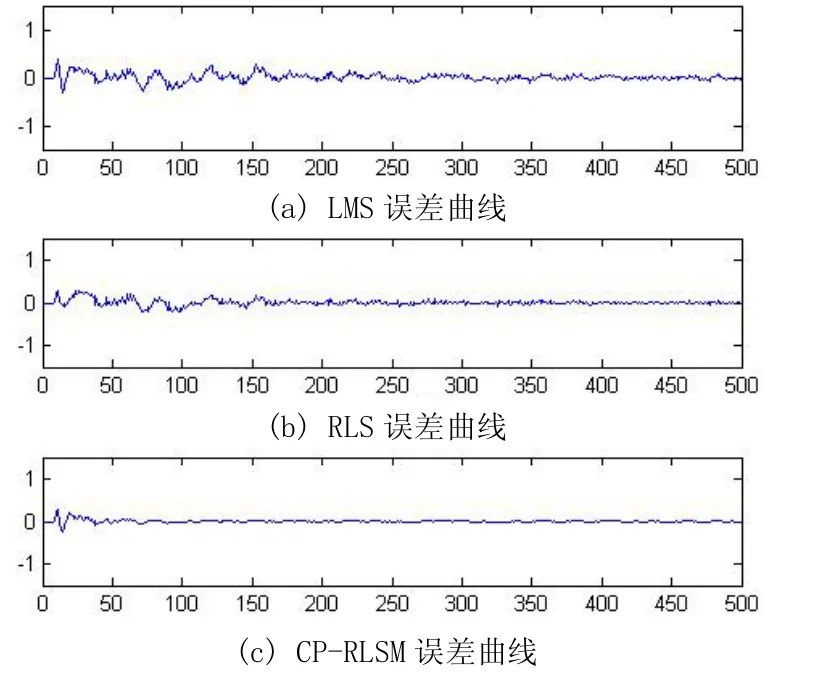
图5 LMS、RLS、CP-RLSM算法误差输出曲线
4 结语
这里分析和讨论了 LMS、RLS自适应滤波算法在收敛速度和稳态失调方面的矛盾以及算法的优缺点,提出了组合比例自适应滤波算法,通过组合比例调整算法的性能,来获得稳定的回声消除效果。组合比例算法首先分别分析各自的误差之后,再利用最小帧误差能量作为判决依据来组合一种最优比例算法作为输出。MATLAB[5]仿真结果表明,该算法在保持更快收敛速度的同时,能获得更好的稳态性,其性能比LMS与RLS两种算法都优。该算法不仅性能优,而且具有开放性,进一步拓展组合越多具有互补性的自适应滤波算法,其收敛速度越快,稳态性越好。
参考文献
[1] 西蒙.自适应滤波器原理[M].北京:电子工业出版社,2006.
[2] 何振亚.自适应信号处理[M].北京:科学出版社,2002.
[3] 刘世金,张榆锋,龚璞,等.NLMS与 RLS算法的仿真比较及其在 FECG提取中的应用[J].计算机仿真,2006,23(04):78-80.
[4] Steven L G.Telecommunication Jacob Benesty, Acoustic Signal Processing for[M].Boston:Kluwer Academic Publishers, 2000.
[5] 陈怀琛,吴大正,高西全.MATLAB及在电子信息课程中的应用[M].北京:电子工业出版社,2002:124-223.
