腔体滤波器的频率计算
2011-03-06马军昌魏文珍
马军昌,魏文珍
(西安富士达科技股份有限公司,陕西 西安 710077)
0 引言
滤波器是一种二端口网络。它具有选择频率的特性,即可以让某些频率顺利通过,而对其它频率则加以阻拦[1],目前用于在雷达、微波、通信等部门,常见有螺旋振子滤波器、微带滤波器、交指型滤波器等等。虽然它们的设计方法各有自己的特殊之处,但是这些设计方法仍是以低频综合法滤波器设计为基础。随着多频率工作越来越普遍,对分隔频率的要求也相应提高,尤其是临近频道的抗干扰[1-2]要求越来越严格,这样常见的滤波器就很难满足。腔体滤波器就是随着通讯技术的发展而产生的新秀,就目前还没有完整的理论来指导其设计。下述理论和方法是工作经验和实践的总结。
1 实例设计
以小灵通滤波器为例来研究腔体滤波器的设计过程。小灵通(PHS,Personal Handyphone System)是数位式行动电话系统,提供高速上网,高清新话质,随着用户量的增大,PHS的网络优化问题也日益尖锐,它采用微蜂窝技术,通过微蜂窝基站实现无线覆盖,要做好网络覆盖问题,就必须做好基站内部的器件指标,滤波器只是其中的一个小部件。指标设定如表1所示。

表1 10 MHz PHS滤波器技术指标
1.1 确定腔体节数
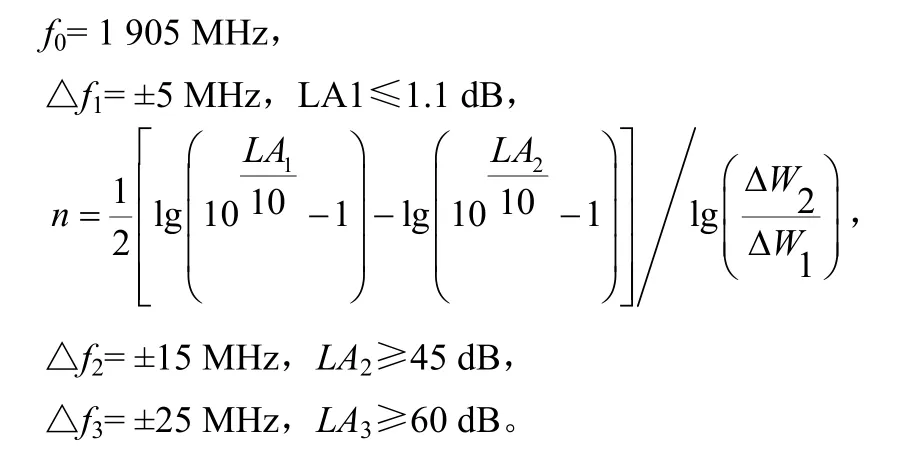
代入 LA1= 1.1,LA2= 45,△W2= 5,△W1= 15,有 n= 5.28;同样代入LA2= 45,LA3= 60,△W2= 15,△W3= 25,有n= 3.378,因此取6腔。
1.2 根据外形尺寸确定单个腔的大小
单腔的排列法有很多种,具体根据输入/输出的位置和需要加的传输零点[3]的情况而定。就如上给定参考尺寸和技术指标的情况下,可以确定必须要有一对腔用来做传输零点,排列方法有图1、图2、图3的基本形式。
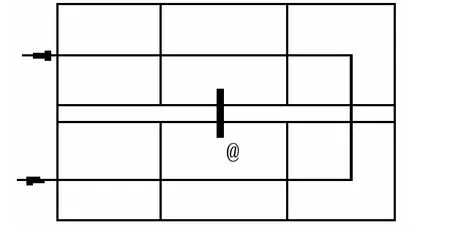
图1 单腔排列
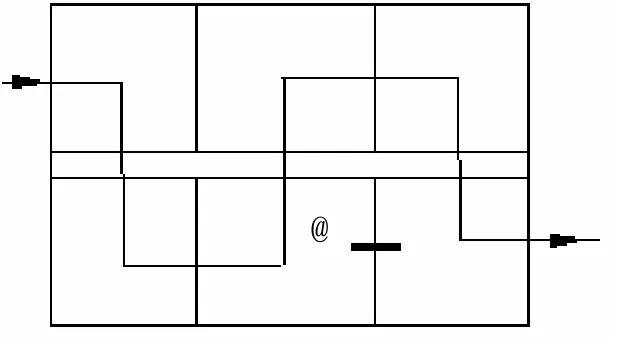
图2 单腔排列
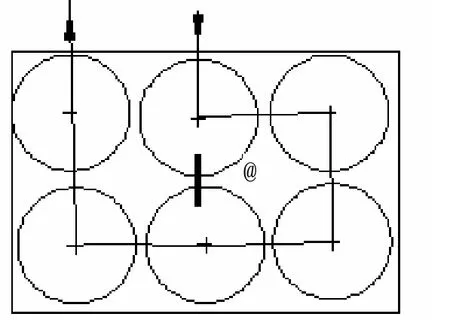
图3 单腔排列
所有图中“@”处为加零点位置;方腔:腔体体积大,电磁容量多;圆腔:单个腔体的摆放更灵活。
1.3 根据Q确定谐振杆的直径
同轴腔的Q值计算公式[4]:

当阻抗是上面值时,理论上的插入损耗可以得到的最小值。在实践中当抽头同样匹配在最佳时只要阻抗[5]在一定范围,都可以得到理想的效果:圆柱腔:55~106 Ω;矩型腔:58~110 Ω。
1.4 腔体、谐振杆直径的确定
通过以上数值的取得就可以确定腔体、谐振杆直径。
①在外形116X80的面上布腔:33.2×33.2的矩型腔;
②阻抗取76 Ω: 可以得出谐振杆直为Φ9.9取整数Φ10。
1.5 谐振杆长度的确定
滤波器总高38 mm.减调谐螺钉高出盖板(锁紧螺母)的高度5 mm,盖板厚度取3 mm,底面留3.5 mm,则腔体净深剩38-5-3-3.5=26.5 mm,谐振杆能产生谐振必须和盖板有一定的距离,无源器件都有功率要求,为避免在系统运行中出现功率打火,谐振杆和盖板的距离应≥0.5 mm,这里暂取2.0 mm,这样谐振杆的长度为26.5-2=24.5 mm。
24.5mm的高度显然不能确定为滤波器的谐振频率,此高度只是它的一个暂定值,至于能不能满足要求,则要通过计算去验证,现进行验证:
同轴滤波器的谐振频率到底怎么计算。很多资料都有提到,但只是一部分即考虑到其平板电容 C=&πD2/4S,即内导体的开路端面与外导体(可看做盖板)之间形成的集中电容、故称加载电容。
在实际中没有不调试的同轴腔体滤波器,这样就会出现图4的情况。

图4 谐振杆剖视
图4通过平板和筒状电容的计算可以得其谐振频率。根据同轴腔的谐振条件:

得出:

其中,L为谐振杆长度(注:这里一定等于腔深);C为光速;Z为阻抗;ωO为频率;Ct为总电容;所以可以求出:

δ为常数;S为内导体的开路端面与外导体之间的距离;m为调谐杆的平均调入深度;Rb为谐振杆的内径;Ra为调谐杆的直径。
代入前面的暂定数据,可得:

所以 Cf= 1.007 5 PF,Cf中暂定 Rb= Φ8 mm; Ra= Φ5 mm,用M5的调谐螺钉。则:

谐振杆的结构如5图所示。
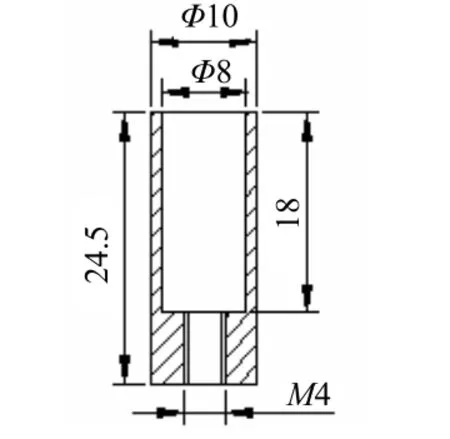
图5 谐振杆
可见只要算出Ct,通过调整S、Ra、Rb和m值,总能找到符合要求的数值.(必须满足:Rb-Ra≥1;S≥0.5 mm)如果 Ct很大, 在保证S≥0.5 mm的前提下,可以通过加大加载电容的方法去满足。如图6所示。在计算阻抗时用图6的Φd;计算平板电容时用图6中的ΦD。

图6 电容加载谐振杆
1.6 窗口的宽度和深度计算
比较繁杂,根据所选择的函数式及波纹,查出它的耦合系数[6]k12, k23, k34,…, kij,再根据公式求出其耦合面积[4],再根据面积等效关系求出它的深度,经过修正得出结果。
ansoft仿真频率结果如图7示,可以看出谐振频率满足(没有加陷波)。
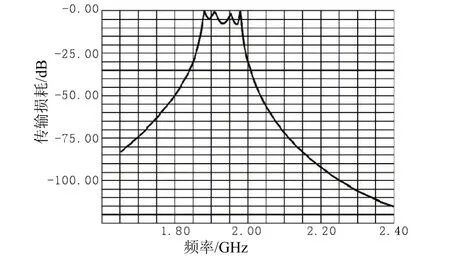
图7 仿真曲线
1.7 实际产品加传输零点后
经过矢量网络分析仪进行调试,得出最后指标,网络分析仪测试曲线如图8示。

图8 产品调试曲线
2 结语
以上方法将比较复杂深奥的微波电磁理论和公式,通过转换,用简洁易懂的计算达到了设计目的,在实际中,通过十几种不同频率的验证,用以上方法是可行的。
[1] 成都电讯工程学院七系.LC滤波器和螺旋滤波器的设计[M].北京:人民邮电出版社,1978.
[2] YOUNG L, SCHIFFMAN B M.New and Lmproved Types of Waffle_Lron Filters[J].Proc.Lee(London), 1968(100): 1191-1198.
[3] 胡皓全,曹纪刚.新型微带交叉耦合环微波带通滤波器[J].电子科技大学学报,2008(06):22-23.
[4] 贺瑞霞.微波技术基础[M].北京:人民邮电出版社,1988.
[5] 程昆仑,李平辉,赵志远.一种宽阻带带通滤波器的设计方法[J].通信技术,2011,44(03):141-142.
[6] 常建刚.高性能滤波器的谐振器结构设计[J] 通信技术,2008,41(12):300-301.
[7] MAKIMOTO M,YAMSHITA S.无线通信中的微波谐振器和滤波器原理论[M].北京:国防工业出版社,2002.
