舰载卫星信道模型的探讨

黄晓飞，徐 池，张海勇，姜凤娇

（①海军大连舰艇学院，辽宁 大连 116018；②大连海洋大学，辽宁 大连 116023）

0 引言

在无线通信链路仿真中最不确定的因素即为无线信道。因此正确地选择信道模型对信道仿真结果的准确性至关重要。对信道模型的研究，传统上集中于给定范围内平均接收场强的预测和特定位置附近场强的变化。海上的通信对抗日趋激烈，简单从功率的角度研究信道已远远不能满足信道建模需要。这里结合舰载通信装备实际情况，对Rummler模型和经典的平坦衰落模型的波形级仿真进行了推导和探讨。

1 无线信道衰落机制

当移动台远离发射机时，当地平均接受场强逐渐减弱，该平均接收场强由大尺度传播模型预测。当移动台在极小范围内移动时,可能引起瞬时接受场强的快速波动，即小尺度衰减。其原因是接受信号为不同方向信号的合成。由于相位变化的随机性,其合成信号的变化范围很大。在小尺度衰减中,当接收机移动距离与波长相当时,其接受场强可以发生4个数量级的变化[1]。

信号参数（带宽、符号间隔等）与信道参数（均方根时延和多普勒扩展）决定了不同的发送信号将经历不同的小尺度衰落。无线信道中的时间色散与频率色散可能产生四种显著效应，这些是由信号、信道及发送速率的特征引起的。当多径的时延扩展引起时间色散和频率选择性衰落时，多普勒扩展就会引起频率色散以及时间选择性衰落。这两种传播机制彼此独立。

如果信道带宽大于发送信号的带宽且在带宽范围内有恒定增益及线性相位，则接收信号就会经历平坦衰落过程；如果信道具有恒定增益和线性相位的带宽范围小于发送信号带宽，则该信道特性会导致接收信号产生频率选择性衰落。

根据发送信号与根据信道变化快慢程度的不同，信道可分为快衰落信道和慢衰落信道。在快衰落信道中，信道冲激响应在符号周期内变化很快。即信道的相干时间比发送信号的信号周期短。多普勒扩展引起了频率色散，从而导致信号失真。在慢衰落信道中，信道冲激响应变化率比发送的基带信号的变化率低得多，因此可假设在一个或若干个带宽倒数间隔内信道均为静态信道[2]。

2 舰载卫星信道特点

在通信系统效能评估的信道建模中，经常考虑的信道模型是高斯加性信道。其所谓的通信对抗条件下的情况也只不过是把两条分别只考虑加性白噪声的信道简单处理。在对抗环境下只考虑加性噪声显然是不够的。主要是由于敌方的干扰样式不同，所以接收到叠加后的信号所表现的变化不只是功率上，简单的作功率上的加减处理不能反映接收性能的变化。小尺度衰落建模属于波形级建模，体现了无线信道的复杂性和随机性,反映了经过不同幅度和相位的衰减后的大量传播路径信号的叠加，是研究通信对抗效能的基本问题。因此深入研究信道衰落机制，建立合适的小尺度衰落模型是研究通信对抗效能评估的首要任务。

目前对无线信道已进行了大量的研究，主要集中在接收天线为全向天线的移动信道上。卫星舰载站信道建模与一般移动通信的主要区别有以下几点：①接收机天线不同，移动通信的接收机天线为 360°全向天线，而卫星舰载站使用的天线为抛物面天线；②通信环境恶劣程度不同，无论舰艇在海上航行时还是在港口或岛屿周围航行时都可以认为天线不受遮挡。所以影响舰载卫星设备的主要因素应该是由运动引起的频率色散。海上信道由于遮挡较少，上述可知，可以认为海上卫星信道为快衰落信道。

需要做两点说明：①对快衰落信道的描述，部分参考文献中把小尺度衰落都称为快衰落，其所谓的“快”实际上是相对于大尺度“慢”而提出的，这样会产生歧义，因此不采用这种提法；②一般来说当信道被认为是快衰落或慢衰落信道时，就不用再指它为平坦衰落或频率选择性衰落信道。快衰落仅与有运动引起的信道变化率有关。但是在进行信道建模时一般不从频率色散的角度进行划分，而是按照时间色散划分。

3 Rummler模型

根据不同的应用、频带和物理环境，对一个多径信道存在许多可能的模型。当海况较好时,卫星通信信道可以建模为一个固定信道。在此讨论推导一种针对两个固定天线之间的陆地通信链路的多径模型,即Rummler模型[3]。Rummler模型见图1示。

图1 Rummler信道模型结构

Rummler信道是视距无线信道，其中的多径衰落是由于在某种气候条件下大气层的分层效应导致的。由于舰载站使用了更大的天线，天线视场被限制在一个小的角度内，因而多径分量的数目相应减少。由于天线是固定的，信道特性中的唯一的时变性是大气层条件的变化。这些变化相对于信道带宽来说可以认为是很慢的，因为信道带宽大约是几十兆赫兹。因此，Rummler模型是一个衰落很慢的多径模型，这个模型广泛用于两个固定点之间频率范围在2～18 GHz的地面微波通信[2]。

3.1 信道数学模型

在给定链路的集合长度和天线参数的情况下，Rummler假定了一个模型，在复数情况下，其形式为：

信道的低通等效传输函数由式（2）给出：

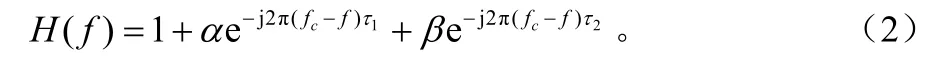
所以，在分析低通等效信道时，可以用f代替(f−fc)，其中 f是低通频率； f≤B/2；B是信道带宽。

为了达到模型参数和经验数据的最佳拟合，Rummler作了几处修正，的一个修正鉴于如下假设：在感兴趣的带宽上，有Bτ≤1，从而导致频率非选择性衰落，因此 e−j2πfτ1≈ 1。

1

式（2）表示的信道可以等效为两径模型：

考虑到要使模型参数符合实验数据，需要在模型中确定一个陷波频率 f0。在 f0上最小。因此令τ2=[(f-f0)/f]τ，其中τ是一个连续延迟。这样就得到了模型的最终表达式：

式中a=1+α，作为整体天线参数；τ是第二路射线的相对路径延迟；2πf0τ和 b=−β/(1+α)是第二路射线的相位和相对幅度。因为式（4）是一个模型不是物理实体，所以只要最终模型是正确的，就可以任意选择参数τ了。已经证明，τ取在(6B)−1量级上，对剩余自由参数的拟合可以很好地表示信道的特征。在这个模型中选择τ=6.3ns。

该模型幅频响应的平方是：

群延迟由相位特性的导数给定：

如果b＜1，因为传输函数仅仅在s平面的左半部有零点，所以它是最小相位的。如果 b≥ 1，传输函数在s平面右半部分有零点，所以他是非最小相位的。低通等效信道的冲激响应，即式（4）的傅里叶变换是：

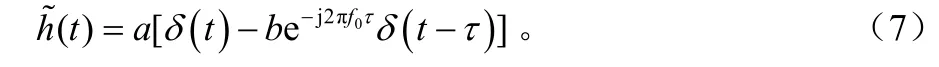
Rummler信道模型结构如图1所示。

参数a和b是随机变量，它们的分布特性由经验分布近似确定，可以用对数形式方便描述。因此，对于最小相位衰落信道，定义：

对于非最小相位衰落信道，b的范围是无界的，可以方便的把式（4）写为[3]：

3.2 参数的概率分布

最小相位和非最小相位衰落出现的概率相等，它们被认为具有如下相同的分布[4]：B1和B2都是指数分布，均值是3.8 dB；参数 A1和A2是高斯随机变量，均值是：

式中，对于A1，B=B1；对于A2，B=B2；A1和A2的标准差是5 dB。注意，由式（9）知，参数a与b是相关的，即A的均值依赖于B。

相位 θ=2πf0τ 分布在[−π,π]范围中，在和具有恒定密度：

陷波频率为：f0=θ/(2πτ)，其中τ=6.3ns。

4 平坦衰落模型

4.1 信道数学模型

当海况较差或者舰艇处于航行状态时，显然Rummler模型不再适用。因此下面讨论一个平坦衰落信道模型[5]。在平坦衰落信道模型中认为到达接收机天线的反射信号分量和散射信号分量的传播时延差相对于符号间隔是可以忽略的，因此接收信号的随机波动可以建模为发射信号和一个合适的随机模型过程的乘积。其结构见图2示。为不失一般性，将输入信号x(t)通过衰落信道后的输出信号y(t)表示如式（11）：

图2 平坦衰落信道模型

式（11）中，n(t)为加性高斯白噪声，d(t)由衰落引起的接收信号的随机波动。由于多径信号是由大量反射、散射产生的，因而有中心极限定理可知,d(t)可用复高斯过程来建模。在任意时刻,其实部和虚部的概率密度函数服从高斯分布,即∶

式中,dr(t)和 di(t)为互相独立的实随机过程.当在发射机和接收机之间存在直视路径时,式(12)改写为：

式中,ρ为直视路径的强度；ωd为直视路径的多普勒频移；θ为直视路径的相位。

经理论分析及大量实测结果表明，当信道的遮挡情况d(t)的包络具有不同的概率分布[6]。当信道中存在一条比较强的直射路径时包络服从莱斯分布；当信道遮挡严重无直射分量时包络服从瑞利分布。研究无线信道的实质就是研究概率分布。相应的瑞利信道和莱斯信道是用于信道建模的两种最经典的概率分布模型。许多科研工作者对经典信道模型做了有利的改进。但考虑到舰载卫星通信装备的实际情况，经典信道模型完全可以满足建模需要。

4.2 瑞利衰落分布

在移动无线信道中，瑞利分布是常见的用于描述平坦衰落信号或独立多径分量包络统计时变特性的一种分布类型。两个正交的噪声信号之和的包络服从瑞利分布。瑞利分布的概率密度函数为：

式中σ是包络检波之前接收电压信号的均方根值，2σ是包络检波之前的接收信号包络的时间平均功率。不超过某特定值R的接收信号包络的包络由相应的累积积分给出：

瑞利分布的均值为：

因此瑞利衰落信号的平均值与中值仅相差0.55 dB。这里所说的中值常用于实际中，因为衰落数据的测量一般在实地进行，此时不能假设服从某一特定分布，采用中值而非均值容易比较不同衰落的分布。

4.3 赖斯衰落分布

当存在一个主要视距传播信号分量时，小尺度衰落的包络分布服从赖斯分布。这种情况下，从不同角度随即到达的多径分量叠加在静态的主要信号上。包络检波器的输出端就会在随机多径分量上叠加一个直流分量。主要的信号到达时附有许多弱多径信号，形成莱斯分布。

莱斯分布概率密度函数为[7]：

参数A指主要信号幅度的峰值，I0(⋅)是0阶第一类修正贝赛尔函数。贝赛尔分布常用参数K来描述，K被定义为主信号的功率与多径分量方差之比。K的表示式为（单位：dB）：

参数K是莱斯因子，完全确定了莱斯分布。当A→ 0,K →−∞ dB，且主信号幅度减小时，莱斯分布转变为瑞利分布。

5 结语

根据舰载卫星通信装备的实际情况，对舰载卫星信道进行建模时不能简单的把信道建模为固定信道。为高效率的得到更准确的仿真结果，应分类建模讨论。海况好时，选取Rummler模型对信道进行建模；舰艇航行时选取一种平坦衰落信道对信道进行建模。

[1] RAPPAPORT T S.Wireless Communications Principles and Practice[M].New Jersey:Prentice Hall Inc.,1996:139-192.

[2] JERUCHIM M C, BALABAN P,SHANMUGAN K S.Simulation of Communication Systems: Modeling, Methodology and Techques 2nd ed.[M].New York：Kluwer Aeademic Publishers,2002:451-510.

[3] RUMMLER W D.A New Selective Fading Model:Application to Propagation Data[J].Bell Syst.Tech., 1979,58(05):1037-1071.

[4] BALABAN P.Statistical Model for Amplitude and Delay of Selective Fading[J].ATT Tech.,1985,64(10):2525-2250.

[5] 潘新华，成建波，徐明,等.一种款带航空无限信道的模拟方法[J].通信技术，2010，43（03）：4-6.

[6] 杨美华.一种无线信道复合衰落模型的分析与仿真[J].通信技术，2010，43（08）：94-96

[7] PÄTZOLD M.Mobile Fading Channels[M].England: John Wiley and Sons,2002:27-39.