单电子辐射跃迁选择定则的讨论

牛振风

(河北北方学院理学院,河北张家口075000)

1 引 言

在量子力学和原子物理两门课程的教学中都会遇到电子辐射跃迁选择定则,本文分别采用量子和半经典两种方法,对电子轨道和自旋无耦合情况下的辐射跃迁选择定则加以讨论,使我们对两门课中的电子辐射跃迁选择定则从形式和本质上有更加深入统一的理解.

2 量子方法讨论选择定则

原子对光的发射和吸收是原子体系与光相互作用所产生的现象.原子在光波的作用下,单位时间内由Φk态跃迁到Φm态的几率为:

由此可知,要实现Φk态到Φm态的跃迁,必须满足矩阵元由此可得出原子跃迁选择定则.不为零,即其三个直角坐标系分量 z ,x和y不同时为零时,原子的跃迁几率方不为零.mkmkmk

设原子中的电子在中心力场中运动,不考虑轨道和自旋相互作用情况下,电子的波函数可表示

跃迁选择定则为

即 xn′l′m′lm′s,nlm lms, yn′l′m′lm′s,nlm lms, zn′l′m′lm′s,nlm lms不同时为零.

利用球谐函数的一个递推公式:

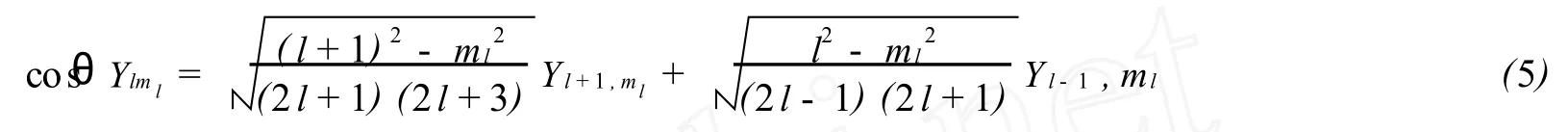
及球谐函数的正交归一化表示式可知, 若使矩阵元 zn′l′m′lm′s,nlmlms≠0, 必须满足:

利用球谐函数的另一个递推公式:

及球谐函数的正交归一化表示式可知, 若使矩阵元 xn′l′m′lm′s,nlmlms≠0,yn′l′m′lm′s,nlmlms≠0, 必须满足:

则为

3 半经典方法讨论选择定则

3.1 角动量的矢量合成

3.2 电子变动组态定则

原子中的辐射属电磁相互作用过程,所以辐射前后体系的宇称守恒.对单个电子,其宇称决定于它的轨道量子数l,当l为奇数时,宇称为寄;当l为偶数时,宇称为偶.用符号 I标记宇称,则在中心场中运动的单个电子的宇称:I= (-1)l,而原子的宇称为原子内所有单电子的宇称之积,所以含有个 N电子的原子宇称为

设辐射前后原子的宇称分别为 IN、IN′,因辐射出的光子的宇称为 I=-1,则由宇称守恒定律得 IN=IN′·I=-IN′, 即:

它等价于

这就是关于电子组态变动的定则.

3.3 跃迁选择定则

设电子的轨道和自旋无耦合情况下,在辐射前后的角动量和自旋角动量分别为辐射出的光子的角动量为,其中i=1.在电偶极辐射中角动量守恒

根据角动量的合成公式 (13),可得

由于i=1,则有:

当 l2≥1时,l1=l2+1,l2,l2-1,即

当l2＜1时,由于轨道角动量量子数是大于或等于零的整数,所以 l2=0.由 (18)式得 l1=1,所以有

根据电子组态变动的定则公式 (15),舍去 (19)式中的Δl=0,可得选择定则:

在电偶极辐射前后不但角动量守恒,而且角动量沿场方向分量也守恒:

即

对于光子i=1,mi=0,±1代入上式,得

在电偶极辐射中,由于电偶极算符与自旋无关,所以它恒不改变电子的自旋状态,应用自旋角动量的矢量模型,可以认为辐射前后原子的自旋角动量相同,即:

辐射前后电子的自旋角动量沿场方向分量也守恒:

故有

所以

因此,电子的跃迁选择定则为

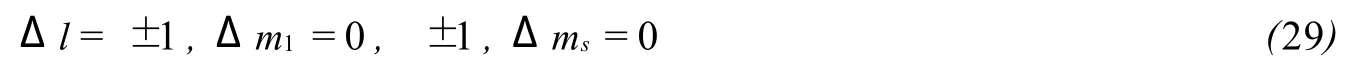
4 结 论

本文用量子和半经典两种方法对单电子辐射跃迁选择定则进行推导,由公式 (11)和 (29)可知得到的选择定则在形式和内容上完全一致.从整个推导过程可看出,量子方法比较严密、完善,而半经典方法则简单易懂.从结论中我们知道并非任何两能级之间的跃迁都是可能的,只有遵从选择定则的能级之间才能实现跃迁.

[1] 周世勋.量子力学教程 [M].北京：人民教育出版社,1979：60-100

[2] 褚圣麟.原子物理学 [M].北京：高等教育出版社,1979：115-190

[3] 曾谨言.量子力学 [M].北京：科学出版社,1981：86-150

[4] 杨福家.原子物理学 (第二版)[M].北京：高等教育出版社,1990：155-215

[5] 张哲华,刘莲军.量子力学与原子物理学 [M].武汉：武汉大学出版社,1997：125-205

[6] 谷震槐.电偶极辐射跃迁的选择定则 [J].西北师范学院学报,1985,(03)：36-38

[7] 郭顾鸿.电动力学 [M].北京：人民教育出版社,1979：80-100

[8] 顾建中.原子物理学 [M].北京：高等教育出版社,1990：65-173

[9] 李平,尹海涛,冯立峰,等.关于选择定则△L=0的研究 [J].东北林业大学学报,2005,33(02)：109

[10] 郝培苓.原子辐射跃迁选择定则的研究 [J].河北大学学报：自然科学版,1991,(04)：82-84