基于软阈值的图像增强
2011-02-28丁西明段汉根
丁西明,段汉根
(1.安徽科技学院工学院,安徽凤阳233100;2.安徽科技学院理学院,安徽凤阳233100)
1 传统的图像增强方法
图像增强的方法很多[1],主要可以分为两大类:空间域增强和频率域增强.空间域增强就是直接对像素值进行操作,频率域增强方法是对图像进行傅里叶变换的操作.常用的空间域增强技术有灰度拉伸、直方图均衡、邻域平均、中值滤波、图像锐化等.频率域增强方法很直观,对图像的平滑主要是减少图像的高频部分,对图像的锐化主要是加强图像的高频分量.频率域的增强方法主要有:低通滤波、高通滤波、同态滤波.从计算效率来看,频率域的实现要比空间域的实现效率高.
2 基于小波变换的图像增强
但是传统的方法在增强图像的同时,也会带来相应的块效应,不符合人们的视觉效果.小波变换是多尺度多分辨率的分解方式[2],可以将噪声和信号在不同尺度上分开.根据噪声分布的规律可以得到图像增强的目的.
数字图像从根本上可以看成一个能量有限的二维信号 f(x,y),可以通过二维小波变换对其进行分解和重构.对二维信号 f(x,y)进行离散小波变换后,得四个子图像:一个低通图像和三个具有方向性的高通子图像,对低通图像可以继续分解,从而得到 f(x,y)的多级小波分解.分解结果如图1示:

图1 小波变换图像分解
上图表示了图像经过小波变换后分解为低通图像,水平细节图像,垂直细节图像和对角细节图像.其中低通图像表示了图像的低频信息,其余三个图像分别表示了三个不同方向的高频信息.分解后的高频成分中包含着大量的图像边缘细节信息.故可以用各种增强算法来增强不同频率的图像,可以改善图像层次感和视觉效果,改善图像的质量,也可以对某一范围内的频率的系数进行增强,从而实现对图像中感兴趣的区域增强.在具体实现过程中,增强系数可以灵活选取,具体的实现步骤为:
1)读入原图像.
2)对原始图像进行小波分解,得到低频成分和高频部分 (细节成分).
3)对高频系数进行非线性增强,这样达到了去噪并增强的目的,其函数如图2所示.其函数满足:
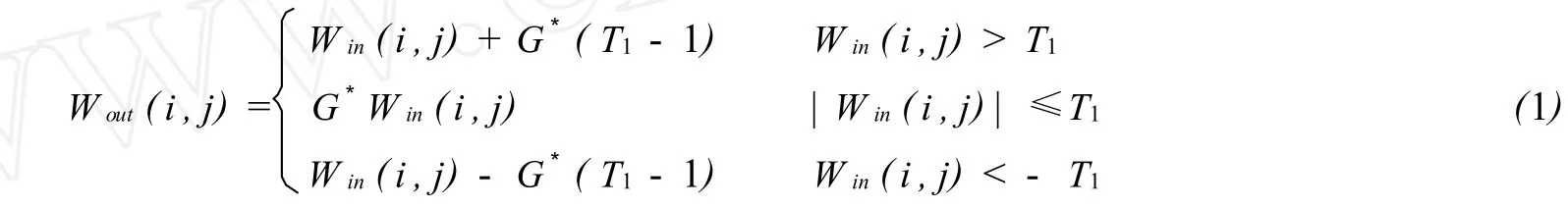
其中G是小波系数增强倍数,T1是小波系数阈值,Win(i,j)是图像分解后的小波系数,Wout(i,j)是图像增强后小波系数.
4)将处理后的两种小波系数进行小波逆变换,从而得出增强后的图像 (输出图像).
3 基于小波变换的阈值图像增强
由于图像经小波变换后,信号的噪声经常出现在高分辨率图像上,并且小波系数表现为较小的值,而图2的非线性映射函数对所有的系数都进行放大,因此在增强图像的同时又放大了图像的噪声,所以采用硬阈值和软阈值的图像增强函数对图像进行增强处理,以保证在增强图像的同时可以有效地抑制噪声的影响.
3.1 硬阈值增强函数[3]
给定一个阈值 Tj,i,对每一层的小波系数进行变换,认为幅值小于 Tj,i的系数为噪声,进行抑制,而幅值大于 Tj,i的系数,给予提升.即设定一增强系数W i,j,对保留下来的小波系数进行变换,得到:

图2 非线性增强的函数
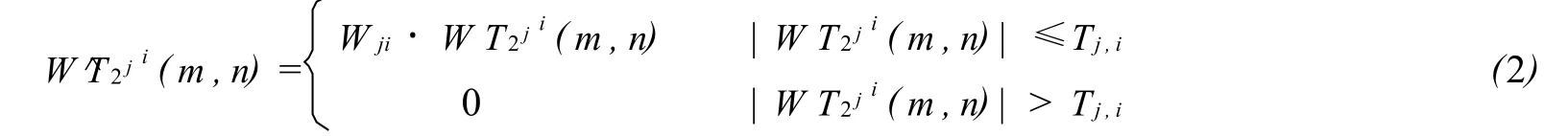
其中W^T2ji(m,n)为处理后的小波系数,Wji为增强系数.这样达到了去噪并增强的目的,其函数如图3所示.

图3 硬阈值增强函数
用硬阈值增强得到的图像,虽然能对图像的边缘锐化,但是图像的像素值集中在某一个区间,不能很好地用到图像输出设备的有效动态范围,输出图像会出现块效应.
3.2 软阈值增强函数[4-6]
给定一个阈值 Tj,i,对每层得到的小波系数按下式进行变换,得到:

其函数如图4所示:

图4 软阈值增强函数
该方法在增强图像的同时,能较好地抑制图像的噪声,较好地保持图像的边缘细节.
4 实验仿真
下面对图像分别采用小波非线性增强和小波软阈值增强方法

图5 小波变换图像增强图
从上图可以看出,传统的小波增强图像算法在放大边缘信息的同时,不能很好地抑制图像噪声.而基于软阈值增强算法克服了传统小波算法中噪声过增强的问题,同时还保持了边缘的细节信息.
5 结 语
给出了基于小波软阈值的图像增强算法,实验结果表明,通过软阈值增强的图像在没有增加计算量的同时更加符合人类视觉效果.图像增强还是数字图像处理中没有完全解决的难题,无法实现对图像的完全真实的还原,还存在许多需要进一步探讨和研究的问题,下一步继续探讨小波变换在图像领域的应用.
[1] 阮秋琦.数字图像处理学 [M].北京:电子工业出版,2001:192-199
[2] 彭玉华.小波分析与工程应用 [M].北京:科学出版社,2004:13-56
[3] 潘泉,戴冠中,张洪才,等.基于阈值决策的子波域去噪方法 [J].电子学报,1998,26(1):115-117
[4] Donoho DL.Denoising by soft-thresholding[J].IEEE Trans IT,1995,541(3):613-627
[5] Baraniuk RG.Wavelet soft-thresholding of time frequency representations[EB/OL].http://eeexplore.ieee.org/xpl/freeabs all.jsp?arnumber=413277
[6] Liu B,Wang YY,Wang WQ.Spectrogram enhancement algorithm:A soft thresholding-based approach[J].Ultras Med Biol,1999,25(5):839-846
