漳浦县旧镇梅宅村海水入*侵的动力系统模型研究
2011-02-26蔡建堤
蔡建堤
(福建省水产研究所,福建 厦门 361012)
漳浦县旧镇梅宅村位于福建省南部沿海。降水量一般年份全年降水日数100多天,1-3月份常有小雨,4-6月份多雷阵雨,7-9月份常有台风暴雨,10-12月份少雨。鹿溪是旧镇主要河流,鹿溪在入海处设有水闸,用于排洪水和含蓄淡水,断开和海水的直接联系。
漳浦县旧镇梅宅村一带有上千亩的池塘围垦养殖,当地养殖户大量抽取地下水进行水产养殖。长期不合理和过量开采地下水,造成海水入侵淡水含水层,养殖区附近的地下水海水入侵十分严重,且入侵有进一步加深的趋势。因此我们加强对地下水资源的监管和建立海水入侵的有效预警机制尤为重要。
海水入侵是世界上海岸含水层中十分普遍和广泛分布的污染问题,认识、预测、防治以及含水层管理最好的途径便是进行监测和计算机的数值模拟[1-2,4,8,13]。在海水入侵模拟的数学模型与数值方法方面做了大量的研究工作[5,7,9,14-15],数学模型主要有突变界面模型和过渡带模型两种;主要的数值方法,海水入侵水质模型求解方法以有限元方法居多,为了解决求解对流弥散方程所引起的数值弥散及过量现象,所采取的方法有迎风(上游加权)有限差分法或有限元法、交替方向隐式差分或有限元法、特征法和变形网格法、人工弥散加权法及欧拉拉格朗日混合解法(即特征有限元法,简称ELM法)等。但是,这些方法的推广还存在一定困难,特别是在三维情况下,而且在程序中对边界的处理也是十分复杂、费时的。
动力系统模型[16]广泛用于农业、金融、医疗等领域,获得很大的成功。本文首次推导出海水入侵预警的动力系统模型,独创模型参数的求解方法,并对模型参数进行灵敏性检验,建立模型的仿真系统。本模型不需要详细了解:海水入侵过程中交换Na+、Ca2+的运移行为[6,12],咸淡水界面[3,10-11]和海水的潮水变化的影响等复杂问题。通过历年的海水入侵监测数据:地下水开采量和监测站点矿化度等信息,确定模型参数,建立模型,预测海水入侵的发展趋势,提出科学的防治措施。目前,国内有关动力系统模型研究海水入侵的方法未见有报道。
1 资料和方法
1.1 研究区位
受国家海洋局和福建海洋与渔业局的委托,对福建省漳州地区进行海水入侵监测。在漳浦县旧镇梅宅村设1个断面,断面布设站位3个监测站位(海水入侵区,过渡带,人为入侵区),站号分别是1号、2号、3号(图1)。
水样品中矿化度测定,采用重量法(SL79-1994),样品的检测结果,见表1。
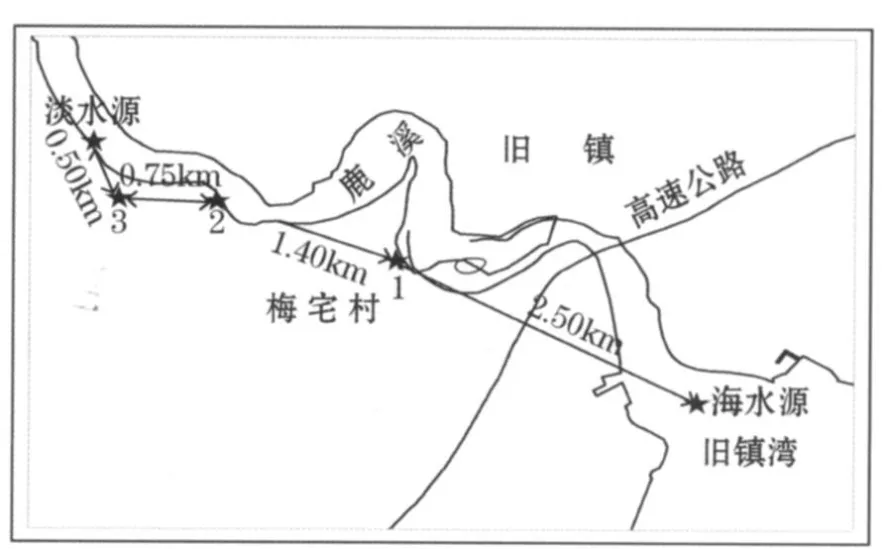
图1 海水入侵监测站位示意图Fig.1 Station locations for seaw ater intrusionmonitoring
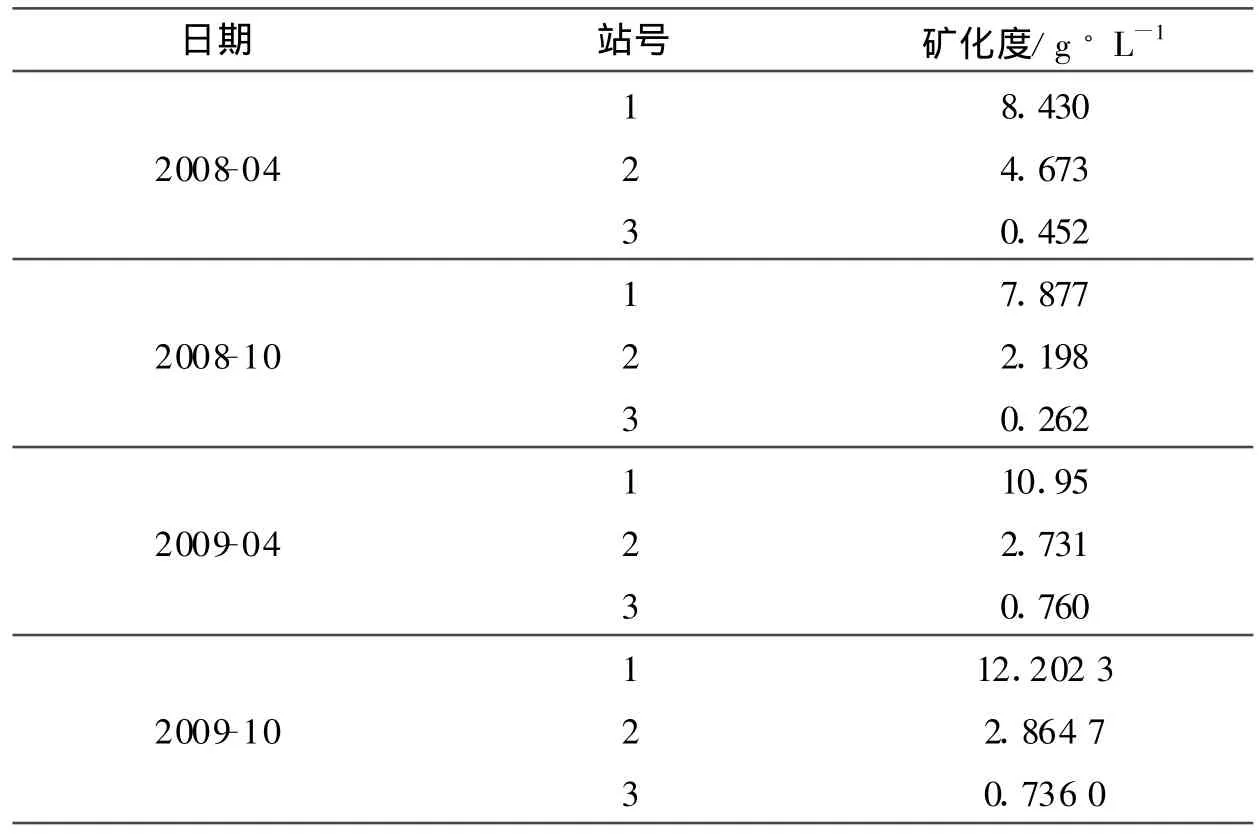
表1 海水入侵监测数据Table 1 Seaw ater intrusion data from themonitoring
1.2 方法
1.2.1 推导模型的数学表达式
漳浦县旧镇梅宅村海水入侵是海湾层状沉积体孔隙式层状入侵,此种入侵取决于咸、淡水之间的平衡状态。一般来讲,阻止海水入侵必须形成一定的淡水水头压力,为此在原有平衡基础上需要有源源不断的淡水供应。咸、淡水之间平衡的破坏主要表现为地下淡水资源量的明显减少,即地下水开采量明显大于地下水在相同时间段内的储积增量,造成咸、淡水相互作用带上的地下淡水水位下降、水头压力不足,不足抵制海水水头压力,导致海水入侵。对基岩海岸海水入侵来讲,也应具备类似上述的地下水动力学特征。因此,淡水水头压力引起监测点淡水水位的变化(∂d/∂t)应该和地下水的水头水位(d)和海水水头的水位(h)有关。淡水水头水位(d)造成淡水水头压力,增大监测点淡水的供应量,使得监测点淡水水位的变化(∂d/∂t)变大,从而抵制海水入侵。由于淡水含水层有一定的水容量,因此,淡水和海水存在竞争关系。当地下水淡水水头水位升高,造成监测点淡水水位的变化(∂d/∂t)变大,使得海水水位(∂h/∂t)变小。同时,监测点淡水水位的变化(∂d/∂t)和监测地点距离淡水水头的距离(x2)有关,离淡水水头越近,淡水水位的变化(∂d/∂t)就越大。
因此,监测点淡水水位的变化和监测点离淡水水头地点(x2)的平方成反比和淡水水头水位d的平方成反比。具有这样性质的海水入侵的动力系统模型为:

式中,α2为淡水扩散率,与淡水密度和水文地质有关;β为淡水含水层资源限制强度度量,与水文地质有关;x2为离淡水水头的距离;k2为抽取监测点的地下水中淡水水位。
同样,监测点海水水位变化(∂h/∂t)的动力系统方程为:

式中,α1为海水扩散率,与海水密度和水文地质有关;β为淡水含水层资源限制强度度量,与水文地质有关;x1为监测点离海水水头的距离;k1为抽取监测点的地下水中海水水位。
海水入侵的动力系统和淡水含水层的实际水位、水文地质、海水的潮汐变化、降雨量、开采地下水的量、地下水赋存条件等很多因素有关,而有些因素我们无法准确的得知。如果建立模型都考虑这些因素,那么将使得模型建立或者求解变得很困难,甚至无法建立或者求解,这样的模型毫无意义。因此,我们应该对模型进行简化。由于海水水量相比淡水水量大的多,监测点抽取地下水用于养殖用,对淡水头水位有较大的影响,对海水头水位影响忽略不计,同时从时间大的尺度(年)上,不考虑海平面变化和潮汐作用影响。另外,式(1)和式(2)中,当地的水文地质情况反映在 α1,α2和β参数,因此,不需要知道实际水文地质。这样简化的动力系统模型,考虑了海水入侵最基本要素的淡水和海水水头水位、水文地质、地下水开采量。这样的模型简单,且有实际的意义,能预警海水入侵。
1.2.2 模型参数的求解方法
随机取一批淡水水头和海水水头的水样,测其矿化度,淡水水头水样矿化度平均值为m,海水水头水样平均的矿化度为n,根据公式:监测点的矿化度=n×c+m×(1-c),求解出海水比例c和淡水的比例(1-c)。通过监测断面各个监测点的观测和测量,取得监测点的矿化度,采水量k1+k2,x1,x2和监测点的水位变化(∂d/∂t+∂h/∂t)。这样,只要利用两个监测点的数据,就可以计算出 ∂d/∂t和∂h/∂t,再利用监测点的淡海水的比例,计算出该监测点的水位大小。根据监测点的水位大小和当地实际海水开始入侵的时间,估算出淡水水头水位(d)。根据Fick化学物体扩散的模型,扩散率和扩散物质的密度有关,假设淡水的扩散率α2=1,则海水的扩散率α1=1.03。这样就可以计算出所有参数h,β,k1和 k2。
2 分 析
2.1 漳浦县旧镇梅宅村动力系统模型的建立
测量海水矿化度的平均值为34.369 5 g/L,淡水矿化度的平均值为0.179 5 g/L。根据公式:矿化度=34.369 5×c+0.179 5×(1-c),算出各个监测站点海水比例c和淡水的比例(1-c),以及淡水和海水的比(1-c)/c(表2)。

表2 淡水海水的比例Table 2 The proportion of freshwater to seaw ater
1号监测站位 x1=2.50 km,x2=2.65 km(图1)。2008年4月-2009年4月,抽水引起的1号监测站位井水水位年变化量为∂d/∂t+∂h/∂t=-0.044 6单位,抽水量年变化量为k2+k1=0.682 0单位,其中1单位=5 m。由式(1)+式(2),得
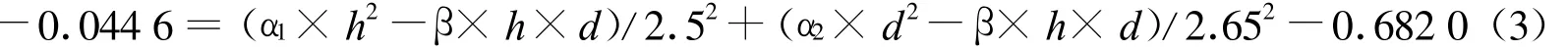
同样,3号监测站位 x1=5.15 km,x2=0.5 km(图1);2008年4月-2009年4月,抽水引起的3号监测站位井水水位年变化量为∂d/∂t+∂h/∂h=-0.100 0单位,抽水量年变化量为k2+k1=4.172 5单位。
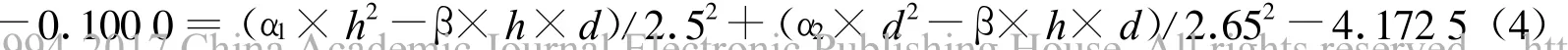
由式(1),(2),(3),(4)得:

d11表示1号监测站位2008年4月淡水水位,h11表示1号监测站位2008年4月海水水位,由表3得:
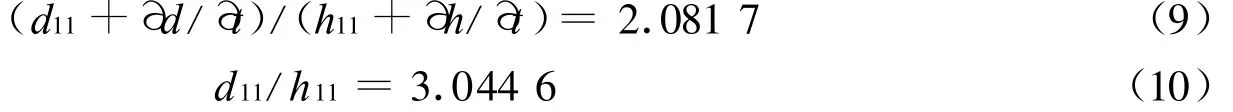
由式(7),(8),(9),(10)得:h11=1单位,d11=3.044 6单位。即2008年监测站位的水位为4.044 6单位。根据Fick化学物体扩散的模型,扩散率和扩散物质的密度有关。假设α2=1,则 α1=1.03,据此估算淡水源的水位 d=5单位。由(5)和式(6)得h=5.121 8单位,β=0.935 6。由式(1),(2),(5),(6),(7),(8)得,k1=0.191 4单位,k2=0.490 6单位。
因此,1号监测站位的动力系统模型方程为:
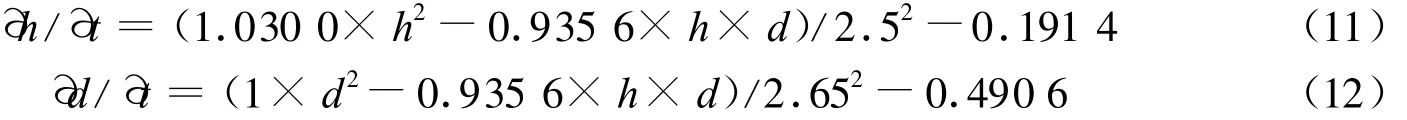
2.2 海水入侵的趋势分析
当∂h/∂t=0的时候,海水停止入侵,假设海水源水位保持不变。如果我们停止开采地下水资源,k1=0,k2=0。由式(11)得出d=5.638 6单位,由式(12)得出 ∂d/∂t=0.189 1。
初始值h=1单位;d=3.149单位,保持淡水水位为5.638 6单位,可以阻值海水入侵,停止开始地下水,经过t=(5.638 6-1-3.044 6)/0.189 1=8.429 4 a后,1号监测站位的井水矿化度淡化为6.243 09 g/L。
当我们停止开采,并让淡水源水位保持在5.638 6单位,经过大约8 a海水矿化度减轻为6.243 0 g/L。因此一旦发生海水入侵,要比较长时间减轻海水入侵,且恢复比较缓慢。
假设我们停止开采地下水,并让淡水水位上升并保持为6.2单位,则∂h/∂t=-0.621 8。
初始值h=1单位;d=3.044 6单位,最高水位 6.2单位,经过 t=1/0.621 8=1.608 1 a,经过大约2 a海水完全淡化。表明:增加淡水的资源可以加速抵制海水的入侵。
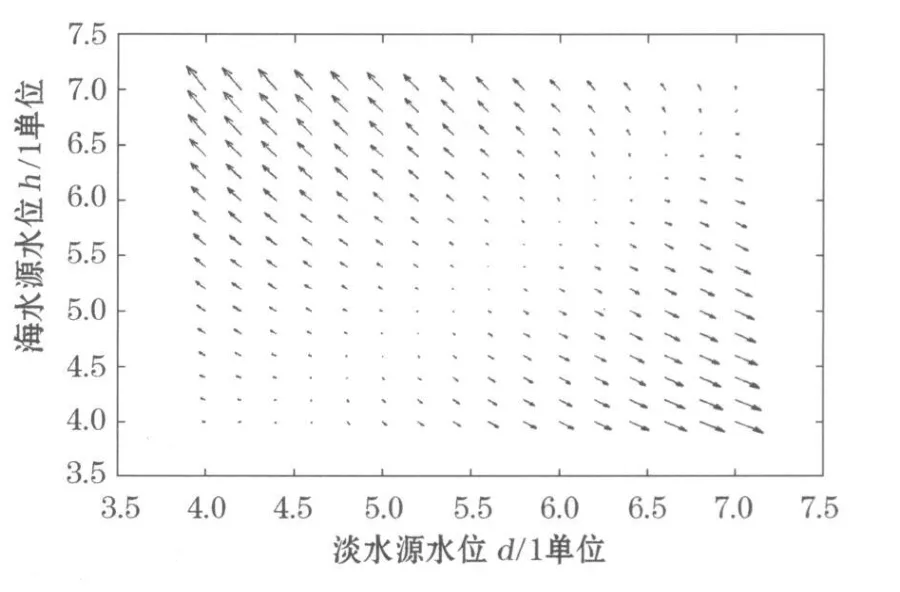
图2 动力系统模型的向量图Fig.2 Vector diagram from the dynam icmodel
动力系统模型的向量图(图2),可以清晰分析漳浦县旧镇梅宅村1号监测站位淡水和海水的变化关系。当淡水水源水位d保持不变,且h>1.100 1×d时,海水水源h越大,向量越大,向量向负的方向,说明第2年1号监测点淡水水位下降越明显,海水的水位则上升明显。再考虑,海水水源h保持不变,且d>1.068 8×h时,淡水水源水位d变大,向量越大,向量向正的方向,说明第2年1号监测点淡水水位出现明显上升,海水水位下降。向量场在h=d附近,向量大小比较小,说明如果保持淡水水源水位和海水水源水位一样大时,第2年1号监测点的海水入侵变化不明显,动力系统到达基本的平衡态。如果增加淡水源水位,使得h>1.068 8×h,则监测点的第2年的矿化度变小,减缓海水入侵。这为我们科学合理的利用地下水资源而几乎不破坏地下动力系统的平衡,提供理论基础。
2.3 模型的预警
采用两种预警方式,静态预警方式:根据当地实际估算第2年的淡水水头水位和地下水用水量等参数(表3)。动态预警方式:根据实际的降水量和地下水用水量,动态调整淡水水头水位和开采量大小等参数(表4)。

表3 静态预警模型方式Table 3 Static prediction model

表4 动态预警模型方式Table 4 Dynam ic predictionmodel
两种预警方式主要误差原因,2010年3-4月漳浦出现大量的降水,增加了淡水的水位,同时用于养殖的地下水开采量也变小,海水入侵减慢。动态预警模式估算的矿化度和实际监测结果比较接近,误差在2%以内,预警精确度比较高。而静态模型主要优点在于能提前对海水入侵趋势做出初步的预测,为水资源的规划和管理提供参考依据,缺点是预测进度比较差,误差在15%左右。
3 讨 论
1)动力系统在建模过程中对一些问题做出假设,我们很少保证这些假设都是完全正确的。因此我们需要考虑模型对每个假设的敏感程度,这就是灵敏性分析,是数学建模的一个重要面。我们不能对模型中的每个参数都计算灵敏性系数,只选择那些有较大不确定性的参数进行灵敏性分析。本模型的推导过程,估算淡水水头水位d=5,并假设α2=1,对于这些假设,我们需要对灵敏性分析,确定对其它参数的敏感程度。
h对d的灵敏性分析,灵敏度分析公式为:

由式(13),当我们在 d=5,h=5.121 8时,由(5)(6)得出:

由式(14)说明:若d增加1.000 0%,将h只增加0.796 6%。说明d的不确定性变化,会导致h的稍微小的变化,但是这样变化不是很明显。
β对d的灵敏性分析,灵敏度分析公式为:

由式(15),当我们在 d=5时,β=0.935 6由(5)(6)得出:
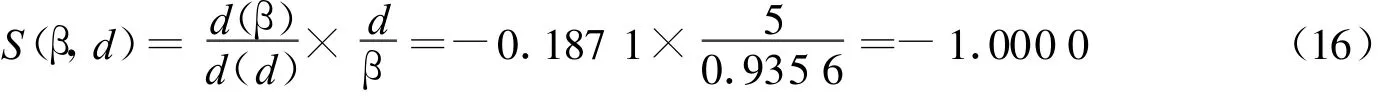
由式(16)说明:若d增加1%,β将大约减少1%。说明我们原始假设的d不确定度,对β成反比,而对h影响成正比。
同样,模型的推导假设α2=1,我们确定与α2相关的主要灵敏性的分析。
β对α2的灵敏性分析,灵敏度分析公式为:

h对α2的灵敏性分析,灵敏度分析公式为:


由式(17),(18)和(19)得:如果 α2增加1%,则 β和h增加均1.043 4%,而 d减少0.960 2%。说明我们原始假设的α2不确定度,对d成反比,而对 β和h影响成正比,且影响的比例一致。
2)应用MATLAB数学软件的SIMULINK对模型进行计算机仿真,通过建模、仿真和分析,可以实时修改参数,减少繁杂的数学运算和推导,对模型的推广有着重要的作用。如:对式(2),建立仿真模型,组建各个模块(图3)。在2个常值信号输入模块d,输入淡水水位d的值;在常值信号输入模块h,输入海水水头水位h值;在2个常值信号输入模块x2,输入离淡水水头的距离x2的值;在常值信号输入模块k2,输入抽取监测点的地下水中淡水水位k2;在常数增益模块a2,输入淡水扩散率α2值;在常数增益模块b,输入淡水含水层资源限制强度度量β值;动态仿真结果就可以在显示输入模块Disp lay1上显示∂d/∂t的值。图3中的参数是按式(12)中的参数输入的,容易得出 ∂d/∂t≅-0.324 6。同样,式(1)的仿真模型和图3大致相同。
d对α2的灵敏性分析,灵敏度分析公式为:

图3 动力系统模型仿真Fig.3 Flow chart for the dynam icmodel
3)模型预警需要通过监测点的水位、矿化度、采水量,预警海水入侵。除了矿化度数据可以精确测量外,水位数据是通过当地的降水量结合井深水位估算、采水量根据养殖户的用水量估算,精确度难以保证。为了获得更为准确的数据,需要改进监测设备,如:采用YSI等自动测定仪器,连续跟踪监测井水的盐度、温度、水深,可以得到更准确和详细的井水开采量和矿化度,从而完善动力系统模型,对精确预警海水入侵有着重要的意义。此外,模型参数在一定程度上反映当地的实际地质特征,因此每个地方参数是不同的,推广应用在其它海水入侵地方需要重新计算参数。动力系统模型是一种新的研究海水入侵的方法,还需要在预警实践中不断地完善。
4 结 论
海水入侵预警的动力系统模型特点:1)模型建立、求解容易;2)模型参数简单:地下水开采量、监测站点矿化度、降水量等信息,不需要了解复杂的水文地质条件;3)采用动态预警方式预警海水入侵,误差在2%以内,精度高。
漳浦县旧镇梅宅村海水入侵的特点:1)要比较长时间减轻目前的海水入侵,大约需要8 a时间,且恢复比较缓慢,矿化度=6.243 0 g/L;2)采用大量增加淡水资源的措施可以加速抵制海水的入侵,如:让淡水水位上升并保持为6.2个单位,大约只需要2 a,监测点完全淡化。3)合理保持淡水水位和海水水位一致,则海水入侵不会加剧。
通过以上综合分析,模型能有效预警漳浦县旧镇梅宅村海水入侵,为我们合理规划和管理水资源提供理论依据。
致谢:参加本项目的人员还有姜双城、陈财珍、洪云、钟硕良,谨致谢忱。
[1] 丁玲,李碧英,张树深.海岸带海水入侵的研究进展[J].海洋通报,2004,(2):82-87.
[2] 王潘平,李天科,王兵,等.莱州湾海水入侵原因分析与防治措施[J].山东农业大学学报:自然科学版 ,2009,(1):93-97.
[3] 艾康洪,陈崇希.漫尾岛咸淡水界面运移剖面二维流水质模型模拟研究[J].勘察科学技术,1994,(6):3-9.
[4] 安永会,张福存,贾惠颖,等.莱州湾滨海平原咸水入侵分析与趋势预测—以山东省广饶县为例[J].环境科学与技术,2009,(5):79-82.
[5] 成建梅,黄丹红,胡进武.海水入侵模拟理论与方法研究进展[J].水资源保护,2004,(2):3-10.
[6] 吴吉春,薛禹群.海水入侵过程中水-岩的阳离子交换[J].水文地质工程地质,1996,23(3):18-19.
[7] 张乃兴,郑新奇,李新运.莱州湾东南沿岸海水入侵发展规律与趋势预测[J].山东师范大学学报:自然科学版,1996,11(4):72-77.
[8] 李国敏.海水入侵研究现状与展望[J].地学前缘,1996,(2):161-168.
[9] 李新运.莱州湾东南沿岸海水入侵相关分析和趋势预测[J].中国地质灾害与防治学报,1994,5(4):20-23.
[10] 姚秀菊,王洪德.黄河三角洲地区地下淡水(微咸水)的形成与演化[J].地球学报,2002,23(4):375-378.
[11] 姜效典,王硕儒.海水入侵地区咸水与淡水分界面计算-B样条函数方法的应用[J].青岛海洋大学学报:自然科学版,1995,25(2):213-220.
[12] 郭笃发.莱州湾东南岸海水入侵区地下水中若干离子的主成分分析[J].海洋科学,2004,(9):6-9.
[13] 黄奕普.海水入侵问题研究综述[J].水文,2003,(3):10-15.
[14] 蔡祖煌,马凤山.海水入侵的基本理论及其在入侵发展预测中的应用[J].中国地质灾害与防治学报,1996,7(3):1-9
[15] 潘世兵,张福存,安永会.咸水入侵趋势预测的非确定模型研究[J].勘察科学技术,1999,17(6):5-8.
[16] M ARK M.Meerschaert.MathematicalModeling[M].北京:机械工业出版社,2005.
