长江口潮波传播影响因素探讨*
2011-02-26路川藤罗小峰陈志昌
路川藤,罗小峰,2,陈志昌,2
(1.南京水利科学研究院,江苏南京 210024;
2.水文水资源与水利工程科学国家重点实验室,江苏南京 210024)
河口是河流与海洋的交汇地带,受径流、潮汐、波浪等因素作用,水流结构较复杂,长江口潮汐作用是影响河口水动力条件的主导因素。潮波传播主要受地形、河口平面形状、径流、底摩阻及科氏力[1]等影响,前人在此方面已有丰硕的研究成果,叶安乐[2]利用考虑摩擦的一维线性流体动力学方程,探讨杭州湾潮波的形成问题,认为断面收缩造成的能量集中是杭州湾潮差增大的原因。修日晨[3]用W.K.B方法求解一维协振潮波在截面积变化水域中阻尼运动的解析解,并将截面积考虑为水深和河宽的二维函数,认为在开阔的浅滩中,最大潮差出现在离岸边一定的距离,而能形成大潮差的喇叭形水域,最大潮差出现在湾顶和湾口之间。随着潮波理论及计算机的迅速发展,潮波数学模型得到快速发展,张金善[4]等建立了平面二维数学模型,分析了长江口风暴潮的特点。姜大荣[5]建立了乐清湾潮波数学模型,分析了乐清湾潮波传播特性。以上数学模型均以N-S方程为控制方程,综合考虑了影响潮波传播的各因素,但未能说明各因素对潮波传播影响的大小。本文概化长江口南支以下地形,通过简单的数值计算来讨论各因素对长江口潮波传播的影响,从而为潮汐河口数学模型的调试工作提供理论依据。
1 河口潮波计算假定
在河口段潮波计算中,做以下基本假定[6]:
1)假定河口口门处的水面周期性升降是已知的,并且是由海洋潮汐引起的。河口内的水体与大洋相比是很小的,所以月球和太阳对河口内水体的引潮力作用可以忽略。
2)河口的几何形状是各式各样的,由河口向内陆,河道断面可能是扩展的,也可能是收缩的,或者先收缩后扩展的。为简化计算,假定河口具有矩形定常断面,或沿程断面变化为纵向距离的某种函数。

表1 河口潮波波长与水深的关系Table1 The relation between tidalw avelength in a estuary and w ater dep th
随着潮波的传播,水质点运动可假定是水平的。潮波波长一般远大于河口段长度。潮波振幅a比波长小的多,和河口段水深比较,一般也可假定是小值。
4)在河口段,水的含盐度在水平及垂直方向均有变化。但进行潮汐计算,可假定水的密度是均匀不变的。
2 模型概化
崇明岛南侧建立概化模型,见图1。因5号和6号断面横跨长兴岛,其断面平均水深远小于两侧断面平均水深,不符合长江口潮波传播实际情况,故假设长兴岛和横沙岛不存在,南北港水域相接。模型上边界取至南北支分流口,下边界取至北槽中,概化后的理想模型见图2,概化模型沿程断面宽度及断面面积见表2。长江口潮汐属于正规半日潮,M2分潮占主导地位,因此分析M 2分潮振幅的沿程变化,能够反映长江口潮波传播规律。本文采用2007年8月长江口水文资料计算调和常数。
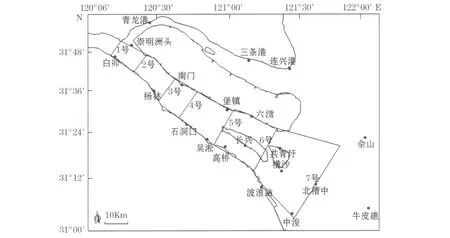
图1 概化模型Fig.1 A model for sim plified topographic outline
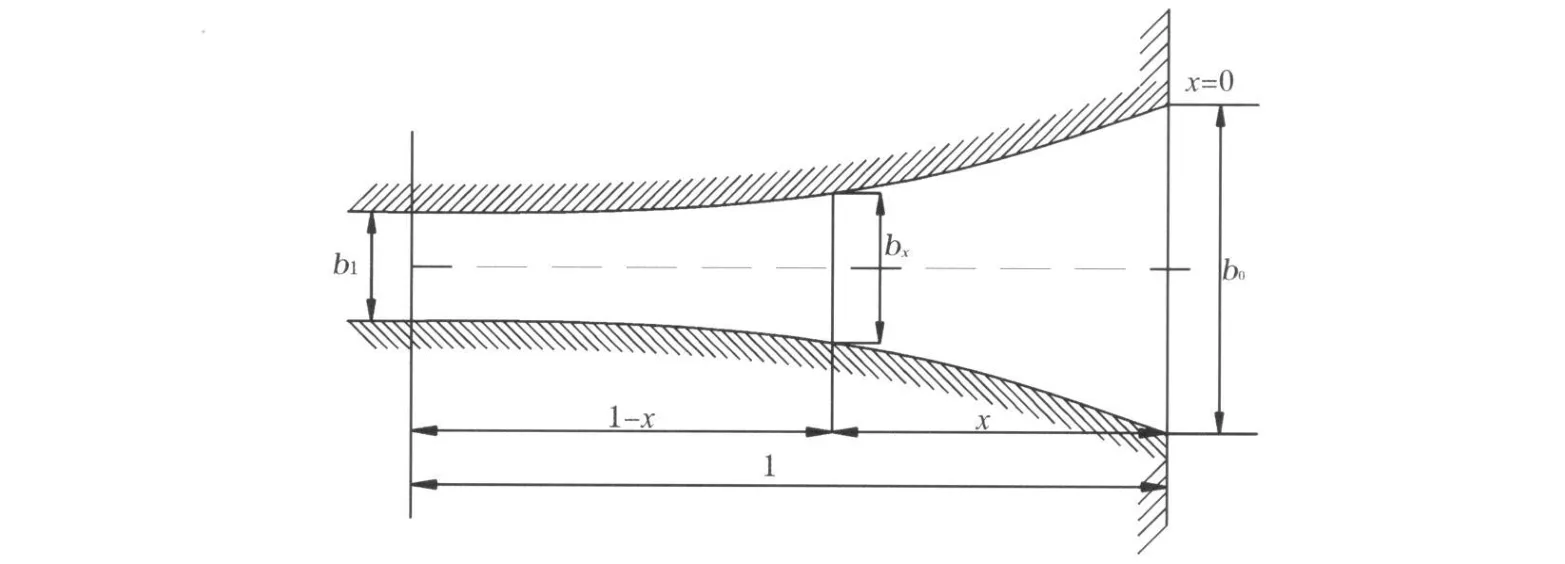
图2 理想模型Fig.2 An idealmodel
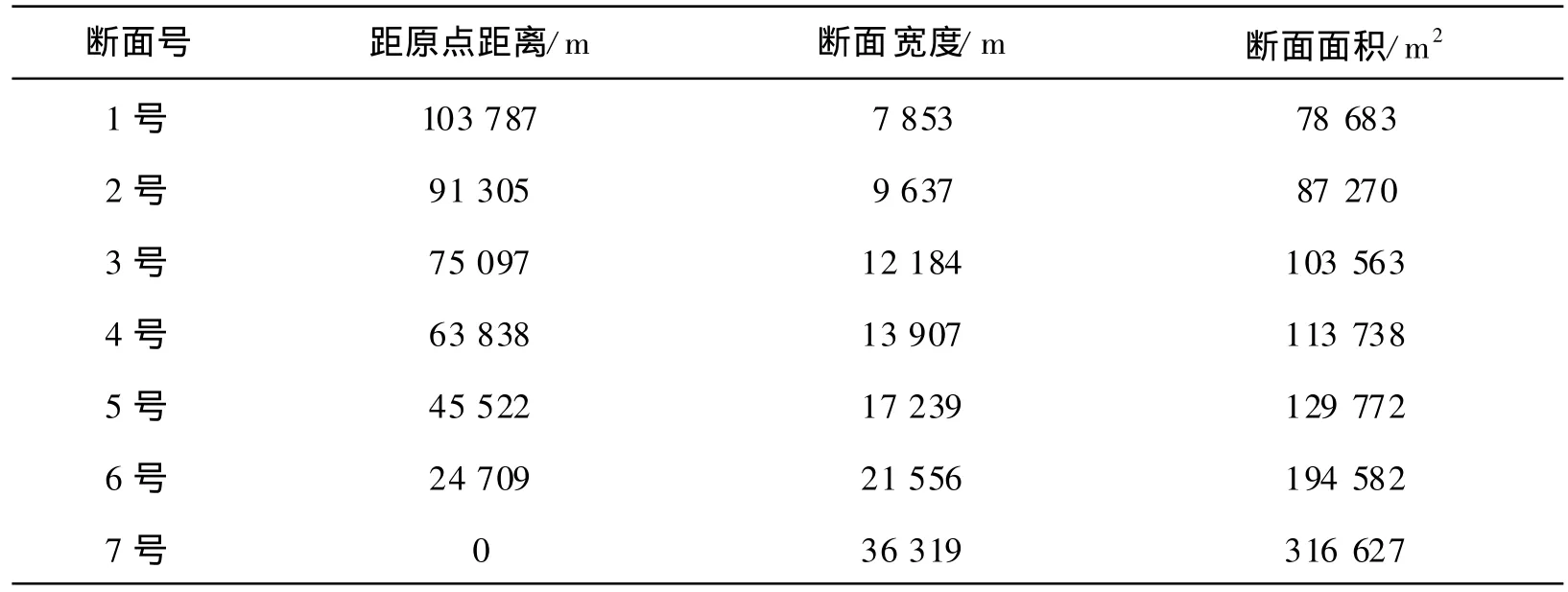
表2 长江口概化模型纵向断面尺寸Table2 The longitudinalvariation of the cross sections in themodel for simplified topographic outline of the Yangtze Estuary
3 概化模型计算
3.1 概化模型(一)——不考虑摩擦渐变宽度等水深河口
图2中,b为河口宽度,x为河口断面距离口门距离,假设河口宽度变化服从指数变化,且bx=b0 e-cx,根据表2,由最小二乘法求得c=3.05×10-5,根据断面宽度及断面面积,由最小二乘法求得平均水深为8.72 m。
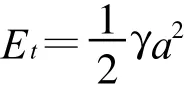
计算结果如图3所示,M2分潮振幅向上游急剧增大,与实际情况差别较大。说明潮波能量在没有损失的情况下,河口宽度缩窄将使能量集中,表现为潮差增大。

图3 模型计算结果Fig.3 Resu lts from themode l calcu lation
3.2 概化模型(二)——考虑底摩擦渐变宽度等水深河口
考虑摩擦的一维线性方程和连续方程为[2,7]:

式中,u为河口中断面潮流的平均流速;η为相对于平均海面的潮位变化;p为线性摩擦系量;B为河口断面的宽度;D为河口断面的平均深度。分潮位和分潮流可以表示成式(2):

式中,Y(x)=H cos g-iH sin g是潮位调和常数振幅H和调和常数位相g的复函数,U(x)=U cosξ-iU sinξ是潮流调和常数振幅U和调和常数位相ξ的复函数。

图4 模型计算结果Fig.4 Results from themodel calculation
计算结果表明(图4),呈指数收缩的河口,水深为常数,只考虑摩擦力的作用,M 2分潮振幅沿程增大,增幅明显小于图3,说明河床底摩擦力损耗了部分潮波能量。但只考虑河底摩擦作用仍然不够全面,计算振幅与实际分析振幅仍存在较大差别。
3.3 概化模型(三)——考虑截面面积变化的潮波传播
考虑截面面积是水深和河口平面宽度的二维函数[3]。取截面积S随x的变化呈指数衰减形式,即S=S0 e-cx,此处c=1.63×10-5。
控制方程仍为式(1),边界条件为:
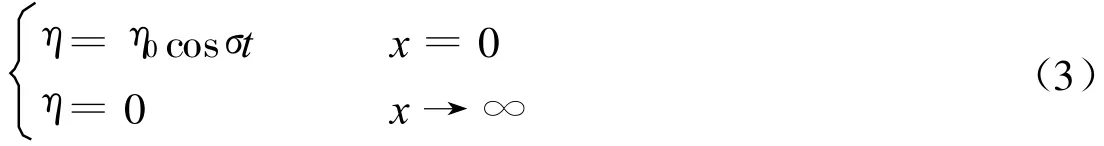
取试解 η=η(x)eiσt,代入式(1)可得 :
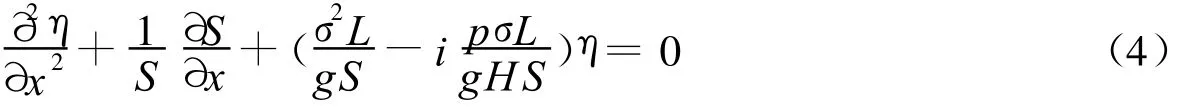
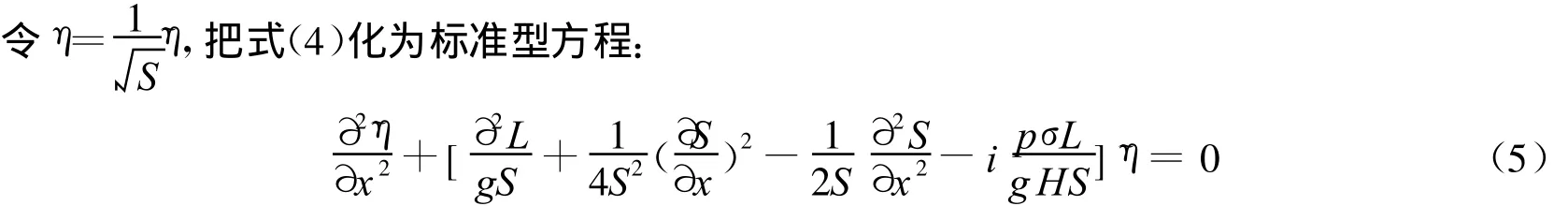
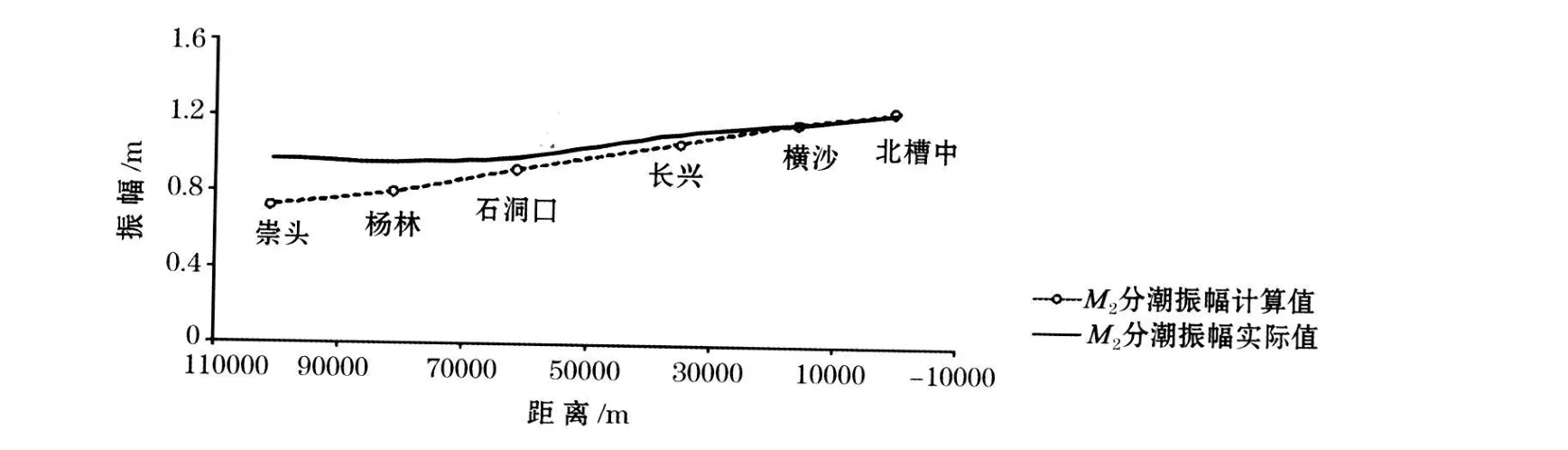
图5 模型计算结果Fig.5 Resu lts from themodel calcu lation
假设截面积S变化很小,根据此假设和边界条件,式(5)的通解为:

式中,A和B为方程的系数;σ为角频率;m、n、ρ为计算过程中物理量合成。计算结果表明(图5),M2振幅沿程减小,但减幅大于实测值。与图4相比,说明断面面积的变化亦是影响分潮振幅的一个重要因素。因模型概化较粗,计算值与实测值仍存在一定的偏差。模型中未考虑潮波反射,故计算值比实测值偏小。
3.4 小 结
3种概化模型的计算结果如表3。由表3知,概化模型(一)计算分潮振幅与实测振幅偏差最大,因其只考虑了河口平面收缩,故可认为偏差完全由河口平面收缩引起。概化模型(二)在概化模型(一)的基础上增加了河床底摩擦作用,与概化模型(一)相比,摩擦的影响仅次于河口平面收缩影响。同理,概化模型(三)与概化模型(二)相比,断面面积变化对分潮振幅影响小于底摩擦的影响。综上所述,在影响长江口潮波传播的主要因素中,河口平面收缩影响最大,其次为河床底摩擦作用,然后是河口断面面积变化。
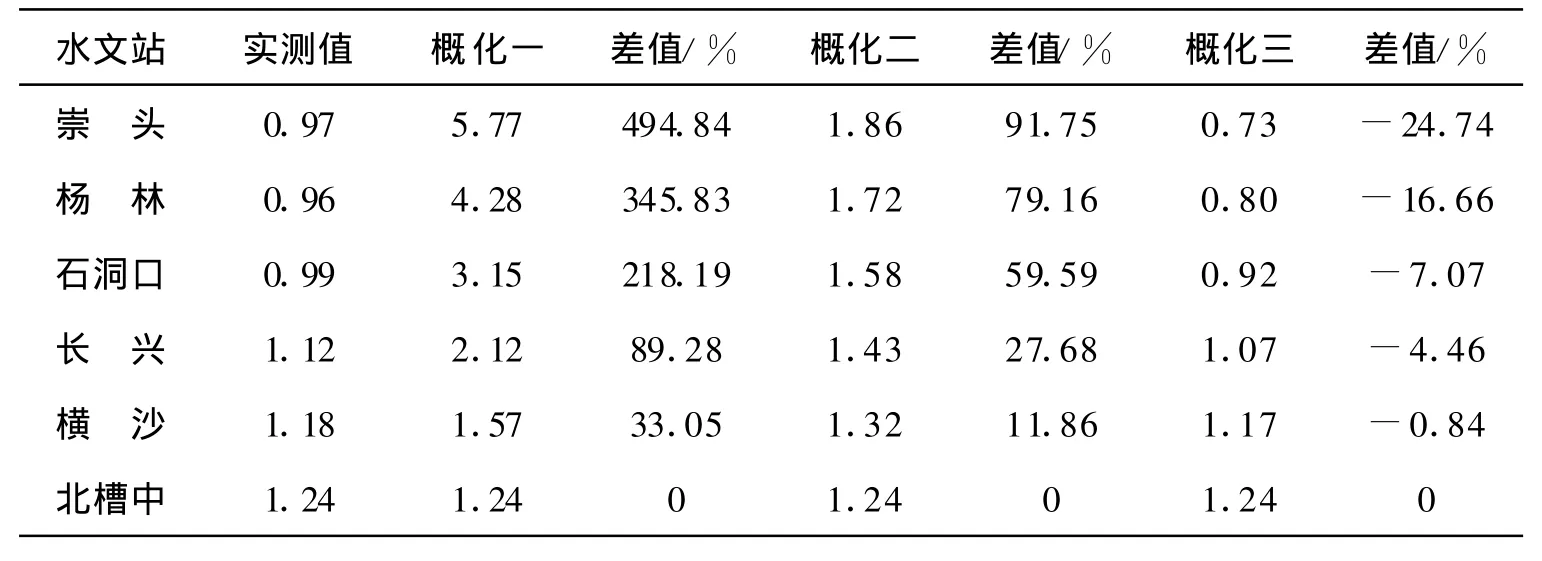
表3 概化模型计算结果分析Table 3 Analysis of the computing resu lts from themodel for the simp lified topographic outline
4 结 论
根据潮波理论建立的3种概化模型,讨论了长江口潮波传播的影响因素。前两种概化模型考虑水深不变,结果无论是否考虑摩擦力,M 2分潮振幅均沿程增加,与实测资料不吻合,说明等水深概化模型不能解释长江口潮波传播过程。因此,考虑了截面面积是河宽和水深的二维函数,建立概化模型,计算结果与实测资料吻合相对较好。
根据3种概化模型的计算结果,在影响长江口潮波传播的主要因素中,河口平面收缩影响最大,其次为河床底摩擦作用,然后是河口断面面积变化。
[1] 吴宋仁,严以新.海岸动力学[M].北京:人民交通出版社,2004.
[2] 叶安乐.杭州湾的潮汐—断面呈指数形式变化的解析模式[J].海洋湖沼通报,1983,(4):9-16.
[3] 修日晨.潮波在截面面积变化水域中传播的探讨[J].海洋学报,1983,5(6):687-693.
[4] 张金善,孔俊.长江河口动力与风暴潮相互作用研究[J].水利水运工程学报,2008,(4):1-17.
[5] 姜大荣.乐清湾潮波变形特点及其数值模拟分析[D].杭州:浙江大学,2007.
[6] 赵今声,赵子丹.海岸河口动力学[M].北京:海洋出版社,1993.
[7] 叶安乐.一种变截面河口中的潮汐效应[J].山东海洋学院学报,1984,14(2):1-11.
[8] 许基义.论河口形状对潮波波高的影响[J].海洋通报,1981,(1):1-8.
[9] 杜珊珊,薛雷平.长江口北支涌潮的一维数值模拟[J].上海水务,2006,22(2):44-48.
