自由活塞式斯特林制冷机压缩活塞间隙密封泄漏的数值模拟

马诗旻 陈 曦 李 静 张 华 袁重雨 祁影霞

(上海理工大学能源与动力工程学院 上海 200093)

1 引言

自由活塞式斯特林制冷机结构紧凑，在低温环境下具有较高的热效率，常用于航天、红外探测、低温物理等领域。目前，自由活塞式斯特林制冷机的压缩活塞与气缸、膨胀活塞杆与压缩活塞内孔，以及排出器与气缸间通常采用间隙密封技术［1－2］。间隙密封是利用密封零件之间的径向微小间隙及该间隙在轴向的一定长度来实现的一种密封形式。相比传统的环密封，间隙密封轴孔两零件采用间隙配合，利用板簧的径向刚度保证零件的定心装配，使两零件无接触。间隙密封减小了轴孔间的磨损、降低了污染，提高了制冷机的寿命。

由于有间隙的存在，当密封两端压力不相等时会引起气体的泄漏，造成冷量损失。对泄漏的分析，通常取活塞轴截面，将流动简化为库埃特流动进行计算。陈曦推导了活塞运动和交变压力波同时存在情况下，环形间隙的泄漏量和一个周期内的平均泄漏量的计算公式，指出泄漏由活塞振动和压差两部分组成［1］。

卢明分析了几种形式的间隙密封的流动特性，并使用Fluent对间隙密封在稳态层流、不可压、定温、定粘度、内外壁面无相对滑动的条件下进行了数值模拟，模拟结果与理论推导非常接近［2］。

在以上工作的基础上，采用数值模拟的方法，计算了交变压力波和活塞振动条件下的泄漏量，并对影响泄漏量的因素进行分析。

2 计算模型

图1为间隙密封的计算模型。该模型作了如下假设:活塞和气缸壁之间没有相对转动，且内外柱面同心，取轴面作为计算区域;L与h相比很大，认为整个流动区域均为层流，且沿着x方向压力均匀变化;忽略质量力的影响;流动为准静态稳定流动［1］。

图1 间隙密封数学模型Fig.1 Mathematical model of clearance seal

计算模型参数为:活塞直径D=40 mm、振幅Xp=10 mm、活塞长度L=70 mm。模型上表面以速度up运动，下表面静止，左右压力分别为p1和p2。

图2为建立的计算网格。在Ansys Workbench中选择Fluid Flow(FLUENT)模块，建立的二维模型并划分网格。设定活塞长度L为70 mm，间隙宽度h为参数P1。由于计算区域为层流，且x方向的梯度远小于y方向的梯度，本着网格与流动相适应的原则，沿x方向划分为高纵横比的矩形网格。

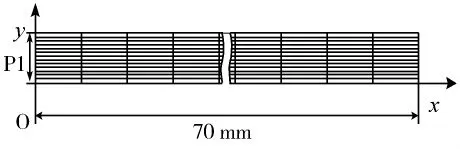
图2 间隙密封计算网格Fig.2 Computational grid of clearance seal

将上述网格导入Fluent，设定计算模型为层流、瞬态。

定义流动气体的参数。在理论计算时，通常认为整个流场中气体的动力粘度μ和密度ρ不变，一般是采用平均动力粘度μm和平均密度ρm。动力粘度μ一般看成温度的函数，在斯特林制冷机的工作温度与压力范围内，氦气的动力粘度 μ在2.03×10－5—2.09×10－5Pa·s之间变化，可以将其看成常数。平均密度ρm的定义为:

式中:p1、p2、T1、T2分别为压缩活塞两端的压力和温度。

上述假设使N-S成为线性方程，简化了计算。数值模拟不受非线性方程的限制，当考虑气体的可压性和气体流动过程中的温度变化时［3］，模拟结果显示:在斯特林制冷机的工况范围内，两者流量差异很小。本着抓出主要矛盾的原则，忽略气体可压和温度变化。设定流体的动力粘度μ为常数2.06×10－5Pa·s，密度ρ等于ρm，按公式(1)由UDF指定。

为模拟活塞振动，设定计算区域上边界为Moving Wall，移动速度由UDF按下式指定:

其中:T为活塞振动周期，φc为活塞位移波与压力波的相位差，t为时间，并设定上边界为无滑移边界。

定义环境压力为充气压力pa;设定左边界表压p1为为背压腔压力，忽略背压腔的压力变化，设为0;设定右边界表压p2为压缩腔压力，通过UDF按下式指定:

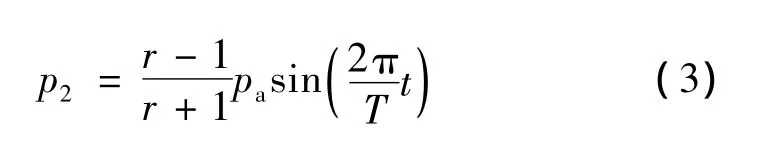
其中:r为压比。

设定时间步长为0.025T，在计算模型的左边界设置表面监视，监视质量流量qm。计算某个时间步时，当监视到左边界的质量流量qm变化不大时，认为该时间步收敛。此时，如果当前时间步所处时刻t大于周期T，则计算一个周期内的质量净流量qnet，m。质量净流量qnet，m的计算方法是将该时间步与前39个时间步的流量求和，再乘以周期T。然后进入下一个时间步的计算。当有连续5个时间步计算得到的净流量变化不大时，认为此时的净流量为当前工况条件下的净流量。

计算了活塞位移波与压力波的相位差φc=40°、密封间隙h=14 μm、频率 f=60 Hz、充气压力 pa=3 MPa、压比r=1.35工况下密封间隙内流动情况，并通过在一定范围内改变上述5个变量中的某一个变量，观察该变量对泄漏的影响。

3 计算结果及分析

3.1 “泵气”现象的模拟分析

图3为间隙密封在1个时间周期T内，体积泄漏流量qv与质量流量qm的变化的曲线，其中:“－”表示流动方向沿x轴负方向。以流量qv=qm=0的水平线为中心线，体积流量曲线以该线为平衡位置作周期震荡。在前后1/2个周期内，流过间隙密封的气体体积相等，方向相反，体积净流量qnet，v为0;而气体密度ρ随压力波变化，在前半周期，活塞右端气体压力大于充气压力，气体密度较大;后半周期，活塞右端气体压力小于充气压力，气体密度较小。密度的变化使前半周期的流过间隙密封的质量流量大于后半周期流过间隙密封的质量流量，质量流量曲线偏离中心线作周期震荡，形成泵气。压缩腔的气体向背压腔泄漏，背压腔压力增大，活塞偏离平衡位置振动，同时压缩腔中的压力波减小，自然频率降低［1］。

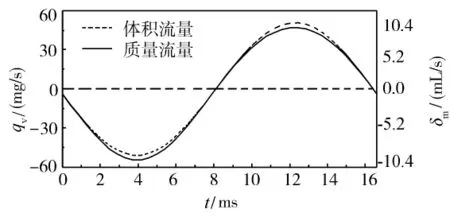
图3 体积流量和质量流量的对比曲线Fig.3 Curves:comparison between volume and mass flow rate

3.2 活塞位移波与压力波的相位差φc对泄漏的影响

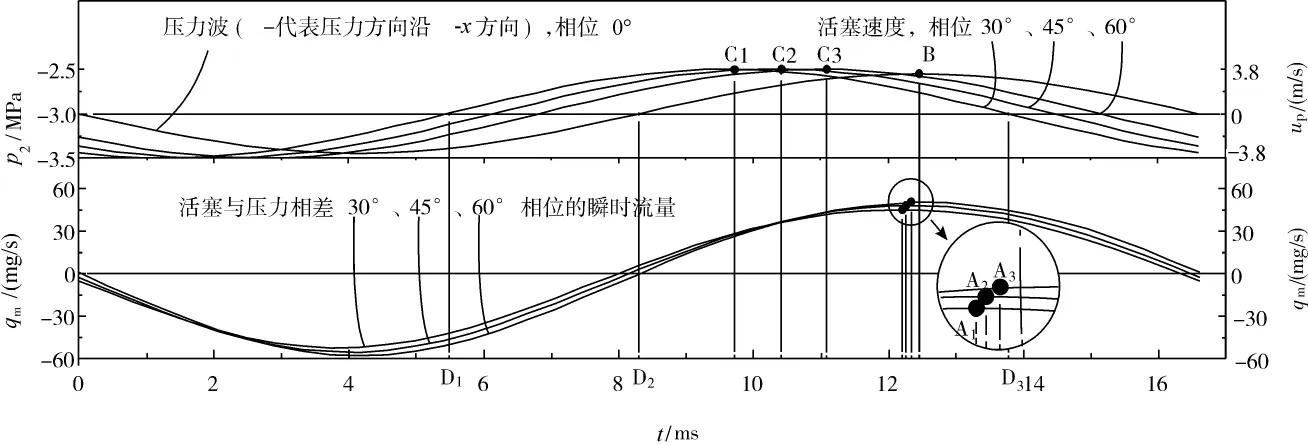
图4 质量流量随φc的变化Fig.4 Curve of mass flow rate with change of φc

图4为1个周期内，活塞位移波与压力波的相位差 φc分别为 30°、45°、60°，质量流量随时间变化的曲线。相位差φc使质量流量出现峰值A1、A2、A3的时刻先于压力波出现峰值B的时刻，但总体影响不大，流量曲线出现峰值的时刻A1、A2、A3与压力曲线出现峰值B的时刻相一致，即压力波在整个流动中起主导作用，活塞运动对流动的影响相对较小。以φc=30°为例，在0—D1ms和 D2—D3ms时间段内活塞速度方向与压力方向相同，活塞运动促进流量的增加;其它时间段内两者方向相反，活塞运动对流动起阻碍作用。在相位差 φc=30°—90°范围内，0—D1ms和D2—D3ms时间段在一个周期内所占的时间比例总是大于50%，也就是从整体上看，活塞运动对流动所起的促进作用大于阻碍作用，即活塞运动促进泄漏净流量的增加。随着相位差φc的增大，D1和D3右移，0—D1ms和D2—D3ms时间段在1个周期内占的比例增加，泄漏净流量增加。当φc=90°时，D1和 D2重合，此时净流量达到最大值。图5是数值计算得到的质量流量峰值(图4中A1、A2、A3)所处时刻与质量净流量qnet，m随相位差φc的变化曲线，在相位差φc=30°—90°范围内。随相位差 φc增加，质量净流量qnet，m增加，峰值时刻推后。

图5 质量流量峰值时间与质量净流量随φc的变化Fig.5 Graph of mass flow rate peak time and mass net flow rate varies with φc

3.3 运行频率对泄漏的影响

图6是不同运行频率f，流量qm随时间t的变化曲线。随着频率f的增加，活塞运动速度up变大。由于在一个周期内，活塞运动对泄漏净流量qnet，m的增加起促进作用，从图7中数值模拟得到的质量净流量随频率的变化曲线看出，净流量qnet，m随频率f的增大而增大。

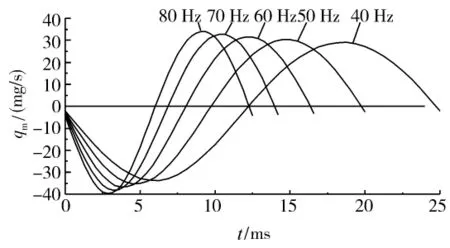
图6 不同活塞频率，质量流量随时间的变化曲线Fig.6 Curves:mass flow rate of different piston frequency

图7 质量净流量随频率的变化Fig.7 Curves:net mass flow rate with change of frequency

3.4 压比对泄漏的影响

图8为不同压比r，质量流量qm随时间t的变化，其中，压比r=1.25－1.45。随着压比r的增加，活塞运动对流动的作用减小，流量曲线出现峰值的时刻推后，向压力波出现峰值的时刻靠近，同时流量曲线的峰值大小增加。图9为质量净流量qnet，m随压比r的变化曲线，随着压比r的增加，质量净流量qnet，m近似线性增加。

图8 不同压比，质量流量随时间的变化Fig.8 Curves:mass flow rate of different compression ratio

图9 质量净流量随压比的变化Fig.9 Curves:net mass flow rate with change of compression ratio

3.5 充气压力对泄漏的影响

图10为不同充气压力pa，质量流量qm随时间t的变化曲线。充气压力pa=1—3 MPa。与压比r的影响类似，质量流量qm随着充气压力pa的变大而变大。图11为质量净流量qnet，m随充气压力pa的变化曲线，充气压力pa变大，质量净流量qnet，m变大。

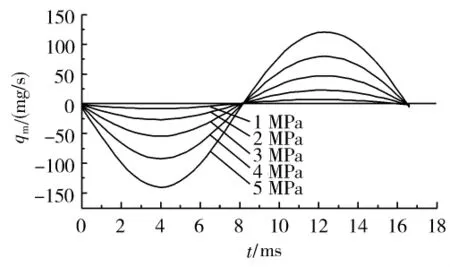
图10 不同充气压力，质量流量随时间的变化Fig.10 Curves:mass flow rate of different charge pressure

图11 质量净流量随充气压力的变化Fig.11 Curves:net mass flow rate with change of charge domination

3.6 密封间隙对泄漏的影响

图12为不同密封间隙h，质量流量qm随时间t的变化曲线。密封间隙h=7—20 μm，泄漏量qm随间隙密封h的增大而变大。图13为质量净流量qnet，m随密封间隙 h 的变化曲线，质量净流量 qnet，m随密封间隙h的变大而变大。

图12 不同密封间隙，质量流量随时间的变化Fig.12 Curves:mass flow rate of different seal width

4 总结

由模拟结果可知:

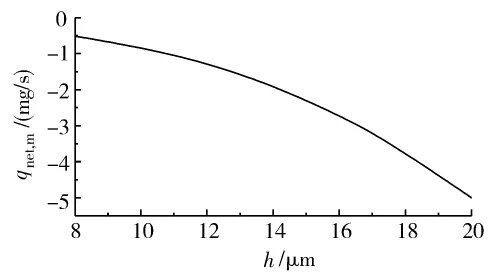
图13 质量净流量随密封间隙的变化Fig.13 Curves:net mass flow rate with change of seal width

(1)在一个周期内，流过间隙密封气体的体积净流量 qnet，v为 0，但气体质量净流量 qnet，m不为 0，净流量方向从压缩腔流向背压腔，背压腔压力将大于压缩腔平均压力，造成压缩活塞向压缩腔一侧偏移振动。

(2)泄漏净流量 qnet，m随间隙宽度 h、充气压力pa、压比r、频率f、活塞位移波与压力波的相位差 φc中任一变量的增大而增大;

(3)通过对比，充气压力pa、压比r以及间隙宽度h对泄漏流量qm和净流量qnet，m的影响较大，而活塞运动的频率f、活塞与压力波的相位差φc对泄漏流量qm和净流量qnet，m的影响较小，即压差是引起泄漏的主要因素;

(4)充气压力pa、压比r以及间隙宽度h任一变量的增加，泄漏净质量流量qnet，m增速变大;活塞位移波与压力波的相位差φc增大，泄漏净质量流量qnet，m近似线性增加，当相位差 φc为90°时，净流量 qnet，m最大;频率f增加，泄漏净流量qnet，m线性增加。

1 陈 曦，武卫东，周志刚，等.自由活塞式斯特林制冷机间隙密封技术研究［J］.低温与超导，2008，36(5):5－8.

2 卢 明.间隙密封式伺服液压缸密封特性研究及仿真［D］.武汉:武汉科技大学，2010.

3 龚 俊，田文静.斯特林发动机气缸与活塞间隙密封的泄漏量分析［J］. 机械制造，2010，48(10):37－39.

4 Bailey P B，Dadd M W，Reed J S.Gas Spring Losses in Linear Clearance Seal Compressors.Cryocoolerl4［M］.Boulder:ICC Press，2007:345－352.

5 Reed J S，Davey G，Dadd M W，et al.Compression Losses in Cryocoolers［C］.13th International Cryocoolers Conference，2004:209－214.

6 Jaime Reed.An investigation of certain thermodynamic losses in miniature cryocoolers［D］.Research report:NSN 7540－01－280－5500，Cryogenics Group，Oxford University，2005:1－29.