基于改进HHT 的水中爆炸冲击波信号时频特性分析方法*

程 擂，韩 焱，王 鉴，杜 娟

(中北大学电子测试技术国家重点实验室，山西 太原030051)

水中爆炸冲击波信号是一种瞬态非平稳信号，特点是持续时间短、频带宽。常用的分析方法有3种:时域分析、频域分析和时频域分析。希尔伯特-黄变换(HHT)［1］是1998 年美国黄锷提出的一种处理非平稳信号、且在实践中得到充分验证的时频域信号处理手段，一些研究者将其应用到了冲击信号等非平稳信号的分析中，并且取得了一定的成果。赖思邈等［2］利用HHT 对水下目标特征进行提取，结果表明HHT 适用于水声非平稳信号的分析，并且有很强的自适应特性和较好的时频聚集性。宋敬利等［3］利用HHT 方法分析了某型舰船在非接触水下爆炸作用下典型部位冲击响应信号，计算了Hilbert 幅值谱、Hilbert 能量谱和Hilbert 瞬时能量，探讨了非接触水下爆炸作用下舰船冲击响应的时频特征。

HHT 处理非平稳信号效果很好，但仍存在一些问题:第1，在低频处会产生一些幅度很小的错误固有模态函数(IMF);第2，在高频处的第1 级固有模态函数，其频带宽度过大，并不是单一组分;第3，由于干扰问题的存在，相邻的IMF 分量不能被很好地区分。另外，HHT 还很容易受到噪声的干扰［4］。

本文中，提出一种改进的HHT 算法，用来对水中爆炸冲击波信号进行时频分析:首先，采用小波分层的方法对信号进行预处理，将输入信号分为多个窄带子信号的结合，使得每一个IMF 为单一组分;第2，采用基于相关系数的IMF 选取原则，对所有的IMF 分量进行筛选，消除错误的IMF 分量。

1 改进的HHT

1.1 HHT

HHT 是一种新的时频分析方法，基本思路是:以瞬时频率为出发点，为了分析信号的瞬时频率，希望把信号分成由有物理意义的瞬时频率的各个信号分量的组合，包括经验模态分解(EMD)和希尔伯特变换［1］2 个部分。

1.1.1 经验模态分解

经验模态分解包括原始信号在连续模式下的信号分解。从原始信号中得到的模式对于信号s 的分解可以写为式中:ci为第i 分量，称作固有模态函数(IMF)，TM是余数。

IMF 需要满足2 个条件:(1)整个数据区间内，极大值和极小值的个数需要相同或者最多相差±1;(2)由每个极小值和极大值产生的包络平均必须为零，而且要求分解到最后时，剩下的余数不能有极值。

首先，找到信号s［n］的极值点，用包络线分别将上下极值点连接起来，得到上包络线u1和下包络线l1，然后算出上下包络线的均值，记作m1。此时m1与原始信号之差

验证是否满足IMF 需满足的2 个条件。若是，则令c1=h1;若不是，则将h1作为原始数据重复上述过程

直到找出符合条件的hk，令其为c1，即求出了IMF 的第1 个分量c1。其次计算

r1(n)仍然包含原始数据的频率信息，因此将r1(n)作为新信号，重复步骤(1)～(4)，循环k 次，直到解出的IMF 分量ck或者残余信号rk非常小或为单调时，循环结束。

1.1.2 希尔伯特变换

通过希尔伯特变换，求出幅度-时间-频率的三维表示。定义一解析信号

式中:SH［n］为s［n］的希尔伯特变换

在极坐标下用指数表示为

根据式(9)即可做出幅度-时间-频率的三维表示图。

1.1.3 希尔伯特边缘谱

定义了希尔伯特谱后，如在时间上对其进行积分，即可求得其希尔伯特边缘谱

与傅立叶频谱相似，希尔伯特边缘谱表示了一个在各个频率处幅值或能量的分布图。

1.2 改进的HHT

针对HHT 的缺陷，首先通过小波分析将原始信号分成不同频段子信号的预处理方法。小波的多分辨分析特性能将信号在不同尺度下进行多分辨率的分解，并将交织在一起的各种不同频率组成的混合信号分解成不同频段的子信号。对于一个N 层分解来说，共有N+1 个途径分解信号。在爆炸冲击波信号中，高频部分为主要分析部分，因此采用如图1 所示的小波分解。其中A 代表高频分量，D 代表低频分量。

通过N 层小波包分解，原始信号被分解成为N+1 个不同频段的子信号，且每一个子信号具有很窄的频带，避免了EMD 分解产生非单一组分IMF 的情况。然而该预处理会使IMF 分量增加，其中会包含许多错误的IMF 分量。

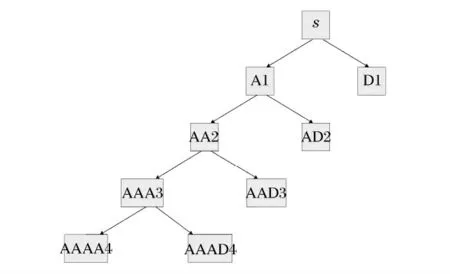
图1 基于爆炸冲击特征的小波分解Fig.1 Wavelet decomposition based on the characteristic of explosion shock wave

理想中正确的IMF 分量将会包含原始信号中所具有的频率成分，因此这些IMF 分量与原始信号应具有良好的相关性。根据这一特性，采用基于IMF 分量与原始信号相关系数的选取原则，来对产生的IMF 分量进行筛选，将低频处幅度很小的错误IMF 以及通过小波包分解产生的错误IMF 去除。设产生的第i 级IMF 分量ci与原始信号的相关系数为ri，根据相关系数的定义，则

设定一阈值ρ，根据ρ 对每一个IMF 分量与原始信号的ri进行对比。若ri＞ρ，则将该IMF 分量保留，若ri＜ρ，则认为该IMF 分量为错误分量，将其去除。ρ 可以通过以下方式确定

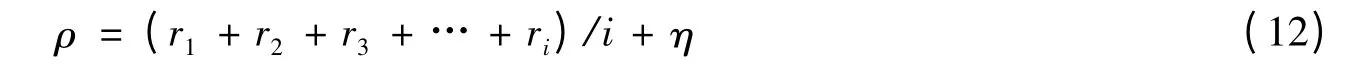
式中:η 的选择取决于所需IMF 分量的程度，ρ 越大，IMF 分量越少，反映的高频信号越明显，但因此可能会丢失某些频率的信息;ρ 越小，所包含高频信号的信息越丰富，但高频信号的反映相对较差。

2 数值模拟与实验

2.1 数值模拟

在上述讨论的基础上，对模拟出的爆炸冲击波信号进行数值分析。爆炸冲击波的数学表达式为

式中:Ps为常数，1≤Ps≤3，b=0.5+Ps;t0可以利用Josef Henrych 的经验公式来计算，即t0=(0.107+0.444R+0.264R2－0.129R3+0.033 5R4)W1/3，其中0.05 ≤R ≤3，W 为炸药质量，kg。

模拟出的爆炸信号如图2(a)所示。图2(c)为加入海洋噪声后的模拟水中爆炸冲击波信号，噪声如图2(b)所示。

对该信号进行HHT，得出该模拟爆炸冲击波信号经EMD 分解后的IMF 分量，信号的HHT 时频表示图如图3 所示。从图3 中可以看出，分量c1包含了高频及低频信息，其频带过宽，不能成为单一组分;分量c6、c7及c8为幅度很小的错误IMF 低频分量。在希尔伯特能量谱的时频表示图中，爆炸冲击波信号的高频部分不能很好地被表现出来，通过局部放大后方可观察到具有高能量的高频信息(如图3(b)放大图中的白点部分)。

图2 模拟爆炸冲击波信号Fig.2 Simulated explosion shock wave

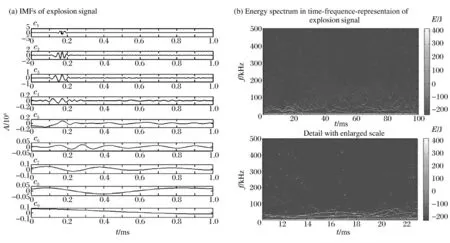
图3 模拟水中爆炸冲击波信号的IMF 及HHT 能量分布时频图Fig.3 IMF and HHT time-frequency representation of simulated underwater explosion shock wave

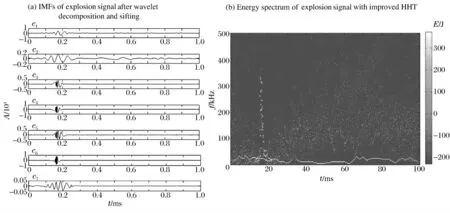
图4 改进后的模拟水中爆炸冲击波信号IMF 及HHT 能量分布时频图Fig.4 IMF and HHT time-frequency representation of simulated underwater explosion shock wave using improved HHT

利用HHT 改进算法对信号进行处理，得出经筛选后的IMF 分量(如图4(a)所示)，对其进行希尔伯特变换，得出改进的HHT 时频表示图，如图4(b)所示。

通过图4 可以看出，经过小波分层以及相关系数筛选后，爆炸冲击波信号的IMF 分量中去除了幅度较小的错误低频分量，在高频部分中频率信号也较为单一，更好地反映了爆炸冲击波信号的EMD 分解。而在能量分布时频表示图中，冲击信号中的高频部分被有效地体现出来(如图4(b)中在10 ～20 ms 处的白点)，通过该图可以看出改进的HHT 算法有效地去除了错误的低频干扰。对比图3 与图4 的IMF 分量以及HHT 能量时频表示图可以看出，改进的HHT 解决了在原始HHT 变换中存在的问题，能够更好地反映出信号的时频特征图。

2.2 水中爆炸实验

图5 所示为水面下70 cm 处，10 g TNT 炸药的实测爆炸冲击波信号，冲击波传感器位于距离炸点2.45 m的同一水平面上。该信号为2008 年11 月于地下目标毁伤技术国防重点学科实验室中北大学爆炸塔处测得。

采用改进的HHT 对该爆炸冲击波信号进行经验模态分解，选取相关系数最高的前10 组IMF 分量，并计算其能量分布时频表示图，结果如图6、7 所示。

图5 实测水中爆炸信号Fig.5 Experimental underwater explosion shock signal

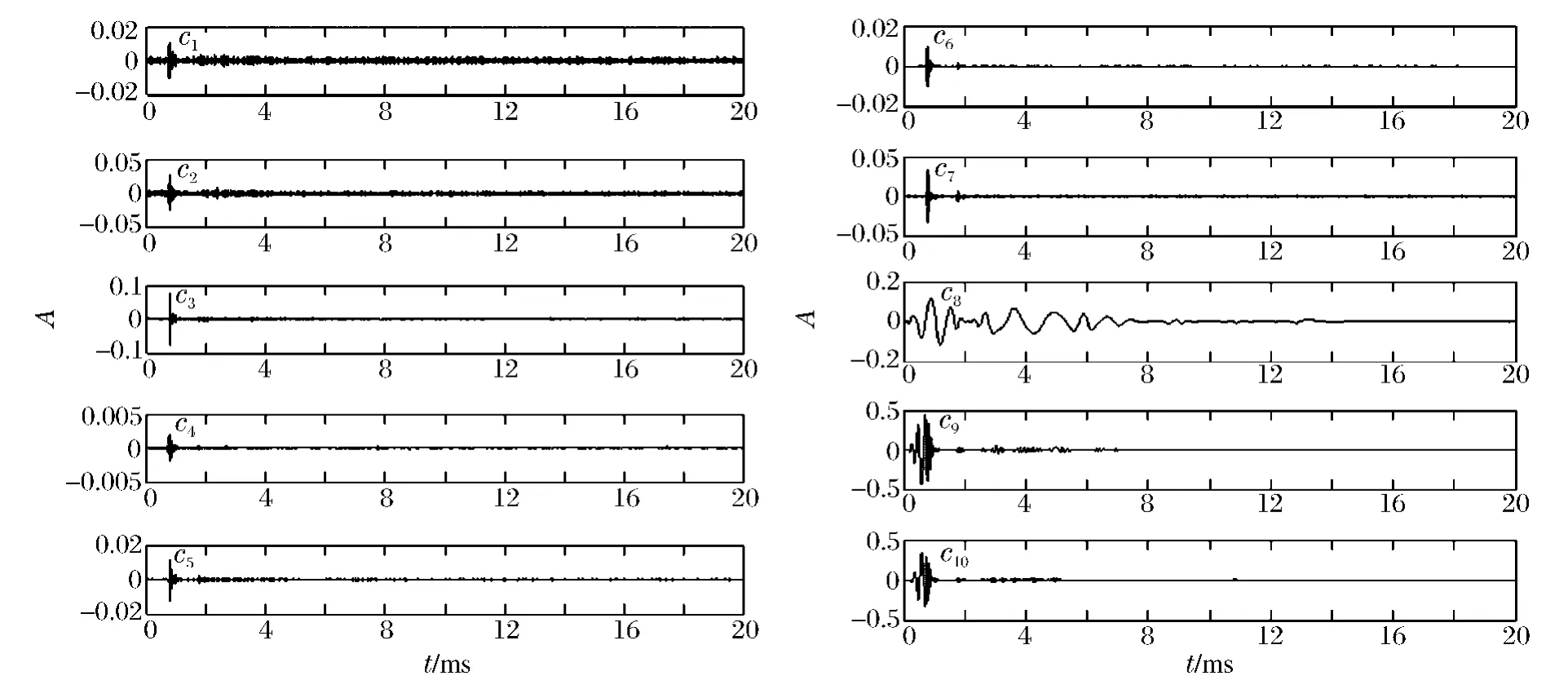
图6 实测水中爆炸信号IMF 分量Fig.6 IMF components of experimental underwater explosion signal

图7 实测水中爆炸冲击波信号的HHT 能量分布谱时频表示Fig.7 HHT time-frequency representation of experimental explosion shock wave using improved HHT

从图6 可以看出，采用改进的HHT 可以有效地得出爆炸冲击波信号中感兴趣的IMF 分量，低频的IMF 分量通过相关系数筛选法被去除，仅仅保留了在爆炸冲击波信号中的高频信号;另外，由于在HHT之前先进行了小波分解，这样高频处的第1 级固有模态函数IMF 分量c1的频带宽度被降低，解决了原始EMD 分解第1 级IMF 分量频带过宽的问题，使得生成的信号能量分布时频表示更为精确有效。在图7的能量分布图中，采用改进的HHT，爆炸冲击波信号的高频部分被更好地反映(如图7 中5 ms 处的时频分布)，由于没有低频IMF 分量以及相邻IMF 分量之间的干扰，信号的时频分布图为进一步的炸点定位、爆炸识别等奠定了更有效的基础。

3 结 论

利用HHT 变换处理非平稳信号的优势，结合小波分解及相关系数筛选法对水中爆炸信号进行处理。结果表明，该方法能够有效、准确地分析爆炸冲击波信号的时频信息，得到爆炸信号能量分布的时频图，为进一步对爆炸信号进行时延估计、效能分析处理等提供了依据。但如果数据量较大时，在EMD进行分解并得出HHT 时频分布图时需要很多时间，因此提高算法的速率将是进一步研究的关键。

［1］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society of London.Series A:Mathematical，Physical and Engineering Sciences，1998，454(1971):903-995.

［2］ 赖思邈，张效民，曹丕.HHT 在水下目标信号特征提取中的应用［J］.电声技术，2009，33(6):36-40.LAI Si-miao，ZHANG Xiao-min，CAO Pi.Application of HHT in feature extraction of underwater target signal［J］.Audio Engineering，2009，33(6):36-40.

［3］ 宋敬利，贾则，张姝红.希尔伯特-黄变换在舰船冲击响应分析中的应用［J］.水雷战与舰船防护，2009，17(3):11-15.SONG Jing-li，JIA Ze，ZHANG Shu-hong.Hilbert-Huang transform and its applications on analysis of ships’shock response［J］.Mine Warfare＆Ship Self-Defence，2009，17(3):11-15.

［4］ Penga Z K，Tseb P W，Chua F L.An improved Hilbert-Huang transform and its application in vibration signal analysis［J］.Journal of Sound and Vibration，2005(286):187-205.