侵蚀滑移计算方法的改进*

张凤国，韩 冰，何长江

(北京应用物理与计算数学研究所，北京100094)

采用拉格朗日有限元程序计算多块材料相接触问题时，如高速碰撞和侵彻问题，在接触面附近往往形成高压、大变形区，滑移线的处理对于接触问题的数值计算结果以及相关物理现象的显示至关重要。二维拉格朗日有限元程序一般将密度较大的物质定义为主块，因为它具有较大的惯性，而相对应的物质定义为从块，在接触面上的节点则分别按顺序分成主点和从点，从而构成1 组滑移线。在计算过程中，当从点侵入到主块中时，把该节点沿与接触面垂直方向拉回到接触面上，同时按动量、动量矩守恒以及速度协调原则调整相关节点的速度。对于与主点相关单元的侵蚀计算问题，一般的处理方法是以累积塑性应变为判据，即当单元内的累积塑性应变大于给定值时，单元内的应力、应变重零，单元失效。采用这种简单的处理方法，一方面常常造成计算数值的不稳定性，即可能有从点侵入到主块中;另一方面在显示物理现象时，主块和从块存在脱离现象以及接触面不光滑。

二维弹塑性流体力学拉格朗日有限元程序LTZ-2D 在计算、分析侵彻问题中得到了较好的应用［1-3］，本文中将LTZ-2D 程序中侵蚀滑移的计算方法进行改进，使程序在模拟侵彻问题的物理现象方面有所改进。

1 主、从节点速度的调整

目前滑移线主、从节点间动量转换的方法有很多种，针对LTZ-2D 程序的特点，本文中采用G.R.Johnson 等［4］的方法。如图1 所示，当从点s 由A 点侵入到由主点i 和j 组成的主滑移线内部B 点时，沿i、j 线的法线方向将B 点拉回到i、j 线上的C 点，并对i、j 和s 节点的法线方向的速度进行调整

式中:ri=0，rj和rs分别为节点j 和s 相对于节点i在r 方向上的距离，tl和ta分别为原来的动量和角动量，mi、mj和ms为节点质量，vi、vj和vs为速度调整后3 个节点上的法向速度。

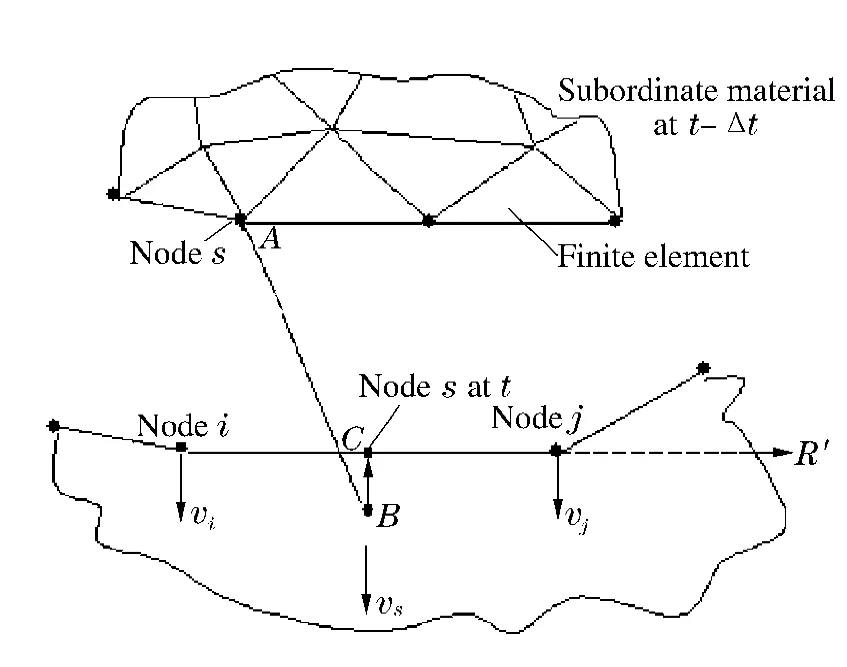
图1 滑移线的处理Fig.1 The method for conserving normal momentum

求解方程组(1)，可以得到

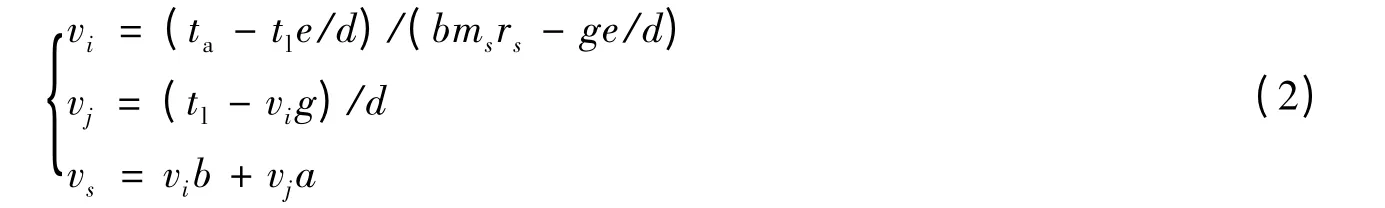
式中:a=rs/rj，b=1－a，d=mj+ams，e=mjrj+amsrs，g=mi+bms。

2 单元的侵蚀计算

侵蚀滑移的计算，包括侵蚀单元的处理，是拉格朗日有限元程序在处理大变形问题时所采取的主要方法之一。G.R.Johnson 等［5］给出了基于累积塑性应变为判断标准的单元侵蚀计算方法，即滑移界面附近的单元的等效塑性应变超过某一给定值时，认为该单元是失效元，其正应力、剪应力置零，等效应变率也置零，并从所属物质结构中删除该单元。目前此方法在有限元程序中应用较广泛，J.J.Pyun等［6］对此方法作了一定的改进。

本文中将滑移线上单元分为3 类，如图2 所示，1 ～9 为滑移线的主点，A ～M 为与滑移线主点相关的单元，对不同种类的单元采用不同的处理方法。

首先，单元只包含滑移线上的1 个节点，如图2 中的B、D、G、H、L 单元;或者虽然单元包含滑移线上的2 个节点，但单元的边与滑移线不重合，如单元I，则与之相对应的滑移线节点包括2、3、5、5、8、5 或7。这类单元不允许被侵蚀掉，即使单元的累积塑性应变超过给定值，否则将造成滑移线数据的不规则，如单元G 被侵蚀掉后，滑移线的节点顺序将变成1-2-3-4-5-11-12-5-6-7-8-9，物质界面内部形成了1 个空腔，这种顺序的滑移线在拉格朗日程序计算过程中很可能造成数值计算的不稳定性［7］。

其次，单元包含滑移线上的2 个节点，并且单元有1 条边与滑移线重合，如图2 中的A、C、E、F、K、M单元，与之相对应的滑移线节点为(1，2)、(2，3)、(3，4)、(4，5)、(7，8)和(8，9)，当这类单元的累积塑性应变超过给定值，并且单元相对于滑移线的角度大于某一值或单元的量纲一硬化因子大于某一值时，单元允许被侵蚀掉。

角度的判据一般取100°～160°之间，这主要根据弹体的初始速度所确定，如图2 中的单元A，相对于滑移线的角1-10-2 大于100°，若单元的累积塑性应变超过给定值，则单元A 被侵蚀掉，而单元E 则不能被侵蚀，即使单元的累积塑性应变超过给定值，因为其相对于滑移线的角3-11-4 为锐角。

三角形单元的硬化因子是指单元的最小高与最长边的比值，它是判断三角形单元形状好坏的重要判据，单元的量纲一硬化因子是指单元当前的硬化因子与单元初始硬化因子的比值，一般情况下取值为0.1，即当单元的累积塑性应变超过给定值，并且其量纲一硬化因子小于0.1 时，该单元被侵蚀掉。

最后，单元的3 个节点依次为滑移线上的节点，此时单元有2 条边与滑移线重合，如图2 中的单元J，其相对应的节点为(5，6，7)，当单元的累积塑性应变超过给定值，或单元的无量纲硬化因子小于0.1，或相对于滑移线的角5-6-7 小于90°时，这类单元将被允许侵蚀掉。

至此，本文中将滑移线的侵蚀标准分为3 类，相应的单元是否被侵蚀掉将根据实际情况分别考虑。如图2 中的单元A 和J 被侵蚀掉，则滑移线由原来的1-2-3-4-5-6-7-8-9，改变为1-10-3-4-5-7-8-9。

图2 主滑移线上的单元种类Fig.2 Classification of the elements along the slideline

3 侵彻问题的数值模拟

将新的滑移线侵蚀判断标准引入到LTZ-2D 有限元程序中，对弹体的侵彻问题进行数值模拟，并与以前的计算结果进行比较。弹体材料为OFHC 铜，弹体半径为12.7 mm，弹体长度为50.7 mm，弹体初速度为2 540 m/s，靶材料为4340 钢，靶厚50.8 mm，靶体半径为76.2 mm，计算采用的是轴对称计算模型，图3 显示的是初始计算模型。

图4(a)～4(b)给出了10 μs 时刻的计算结果，图4(a)显示了采用以前的滑移侵蚀判断标准所引起的接触面处弹体表面出现的凹凸不平的不规则现象，而采用新的标准很好地解决了这一问题，弹体表面显示了很好的圆滑曲线，见图4(b)。

图4(c)显示了采用以前的滑移侵蚀标准所引起的另一种数值模拟的物理现象，即计算过程中显示的物理现象存在弹靶脱离的情况，这显然与实际物理现象存在较大差别，而采用新标准的计算结果显示弹靶可以保持较好的接触，见图4(d)。此外，图4(b)、4(d)显示，采用新的滑移侵蚀判断标准，弹靶的接触表面具有较好的光滑性。

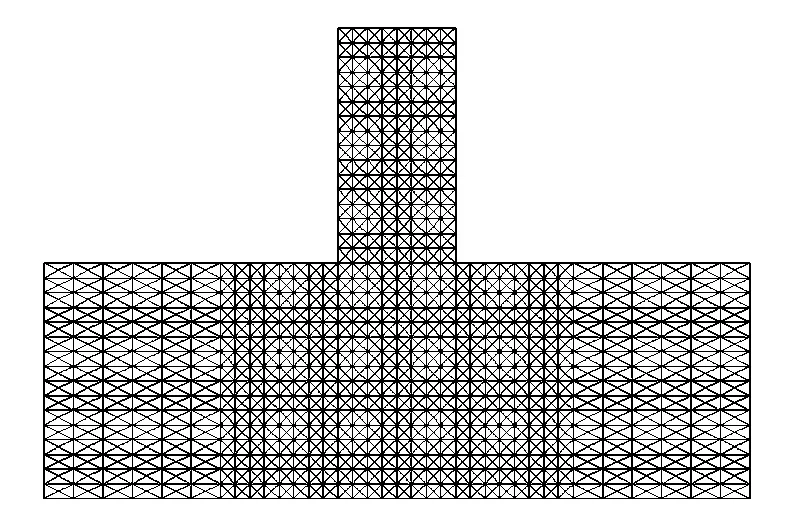
图3 初始计算模型Fig.3 The initial computational model

图4 用不同的方法在不同时刻的冲击计算结果Fig.4 Impact calculation by different methods at different times

4 结 论

对LTZ-2D 有限元程序中的滑移侵蚀算法进行了改进。计算结果显示，采用新的滑移侵蚀判断标准，在计算弹体对靶板的侵彻过程中，弹靶之间不仅可以基本保持接触，而且接触面更光滑，与真实的物理现象更接近，对侵彻过程的数值描述更精细，同时也有助于深入分析弹靶之间相互作用的力学机理。

［1］ 张凤国，李维新，洪滔，等.超高速钨合金长杆弹对混凝土侵彻及损伤破坏的数值分析［J］.弹道学报，2008，20(3):64-67.ZHANG Feng-guo，LI Wei-xin，HONG Tao，et al.Numerical simulation for damage and penetration of concrete driven by long-rod projectile of tungsten alloy under super-high speed［J］.Journal of Ballistics，2008，20(3):64-67.

［2］ 张凤国.动载荷作用下混凝土靶板损伤破坏的数值分析［J］.兵工学报，2009，30(9):19-22.ZHANG Feng-guo.Numerical analysis of the damage of concrete under dynamic loading［J］.Acta Armamentrii，2009，30(9):19-22.

［3］ 张凤国，冯其京，郝鹏程，等.聚能装药侵彻混凝土靶板的数值模拟［J］.计算物理，2009，26(6):887-891.ZHANG Feng-guo，FENG Qi-jing，HAO Peng-cheng，et al.Numerical study on penetration of shaped charge jets into concrete targets［J］.Chinese Journal of Computational Physics，2009，26(6):887-891.

［4］ Johnson G R，Stryk R A.User instructions for the EPIC-2 code［R］.AFATL-TR-86-51，1986.

［5］ Johnson G R，Stryk R A.Eroding interface and improved tetrahedral element algorithm for high-velocity impact computations in three dimensions［J］.International Journal of Impact Engineering，1987，5(1/2/3/4):411-421.

［6］ Pyun J J，Kennedy C M，Hruska D.A new slideline/eroding algorithm for EPIC2［J］.International Journal of Impact Engineering，1990，10(1/2/3/4):473-482.

［7］ Pyun J J，Hamilton C W.A slip/collapse algorithm in a hydro code［C］∥Nichols J A.Proceedings of the Nuclear Explosive Design Physics Conference.New Mexico:Los Alamos National Laboratory，1983:127-150.