间瞄寻的导弹末段最优制导建模与仿真

徐文旭，李召，张更宇

(63961 部队，北京100000)

0 引言

间瞄寻的导弹用于超视距精确打击坦克和低空飞行的直升机等目标。为了保证命中精度，采用分段制导方式，即在中段制导成功的前提下(导引头视场与目标交汇，并成功锁定目标)，再实行末段制导。

长期以来，末段寻的导弹导引律主要针对非机动或机动程度不大的飞行目标进行设计［1］，纯比例导引在这种背景下是一种有效的导引律。然而对于直升机这样的机动目标，采用纯比例导引的导弹会在弹道末端出现较大的视线角速度，当可用过载较小时会产生较大脱靶量。

因此，人们研究了高级导引规律，考虑目标机动对制导精度的影响，并考虑导弹对指令响应的滞后性，这种导引规律对导弹需用过载需求较小，并且产生很小的脱靶量，称为最优制导［2-3］。然而最优制导律在工程实际应用中需要已知目标机动及导弹剩余飞行时间，但目标机动过程很难准确描述。文献［3-4］将目标机动统计特性描述为目标加速度的微分是白噪声，同时导引头的视线角速度量测噪声也是白噪声，并建立最优制导条件下的系统状态模型和测量模型，利用Kalman 滤波算法求解状态模型，能获得较小的脱靶量。

本文则将目标机动统计特性描述为目标加速度的微分是有色噪声序列［5-7］，并建立相应的状态模型，这比统计独立的白噪声序列具有更大的目标机动模式覆盖范围。然后也用Kalman 滤波算法求解状态模型，通过仿真分析目标机动对导弹命中精度的影响，验证该方案在不改变导弹硬件的前提下，提高导弹攻击低空直升机等高机动目标命中精度的能力，为间瞄寻的导弹实现最优制导提供设计参考。

1 最优制导寻的回路

1.1 最优导引律简介

文献［4］在追击或迎击情况下，将弹目相对运动间的几何角度关系线性化，给出了比例导引和扩展比例导引的统一形式。扩展比例导引解决了目标加速机动问题，但当制导系统存在惯性延迟时，仍有较大脱靶量。针对惯性延迟问题，文献［4］164又给出了最优制导律，列出如下(表述形式略有变化):

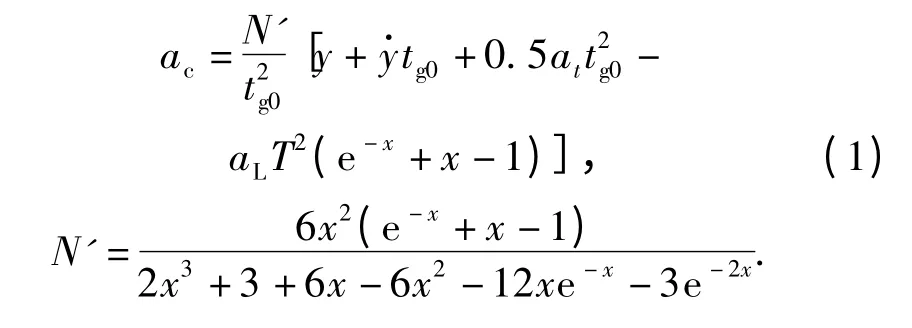
其中:N'为有效导航比;ac为指令加速度;at为目标机动加速度;aL为将ac输入某惯性环节后的输出，满足T(daL/dt)+aL=ac，T 为该惯性环节的时间常数;y 为导弹在惯性参照系中垂直于当前的弹目瞄准线方向的位移向量;tg0为待飞时间，tg0=tmax-t，tmax为总飞行时间;最后，定义

可以看出，最优制导的有效导航比N'与制导时间常数T 和待飞时间tg0有关。若不考虑惯性延迟，最优制导规律就是扩展比例导引规律。若进而略去目标机动加速度，就得到传统的比例导引规律。即便目标有机动加速度并且导弹具有惯性滞后，理论上，最优制导律仍能消除脱靶量。

1.2 最优制导系统状态模型和测量模型

为了实现最优制导，必须已知目标的加速度信息，这对导引头的测量能力提出了很高的要求。将Kalman 滤波技术应用于最优制导寻的回路，能够及时获得目标加速度的估计信息而不必增加测量硬件。

在将目标机动统计特性描述为目标加速度的微分是有色噪声序列［5-7］情况下，Kalman 滤波估值的制导系统状态方程为

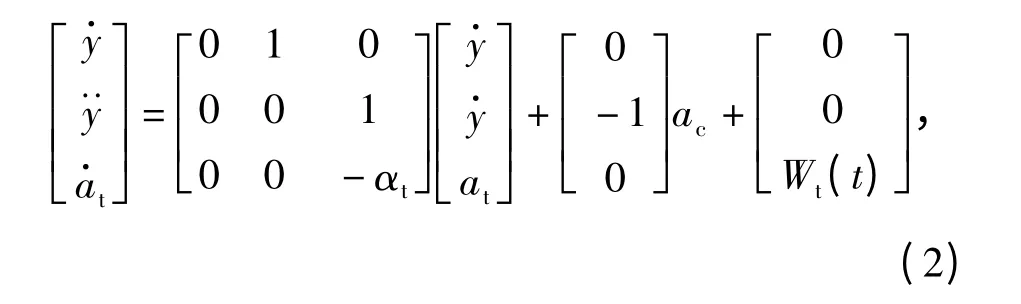
其中，与式［4］中的相应方程不同之处在于第三行，即目标机动的模型结构为1 阶马尔柯夫过程的时域动力学方程

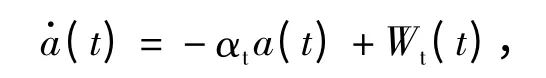
其中，Wt(t)是与机动加速度相关的白色噪声，且满足

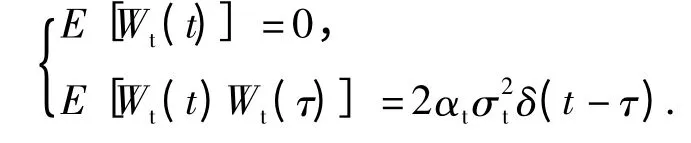
即Wt(t)的方差强度为2αtσ2t.

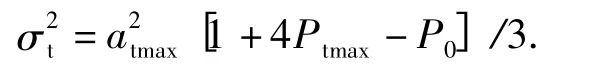
atmax为最大机动加速度，其发生概率为Pmax，非机动发生概率为P0;αt=1/τt，τt为机动相关时间常数，通常取经验值，如果目标为较慢的持续机动，取τt=60;如果目标做快速的短暂机动，取τt=10.

导引头量测方程为

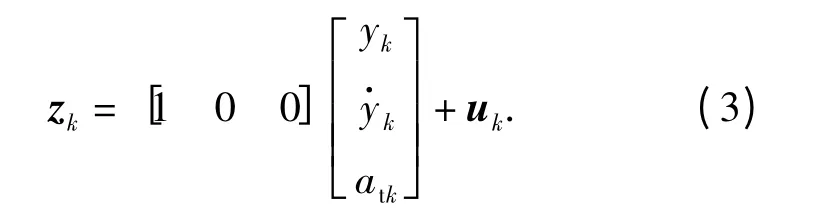
通常导引头只能测出视线角λk，λk的值带有量测噪声，将之与弹目距离的估值vctg0相乘，得到带有噪声的伪测量值zk.

设定uk为白噪声，标准差由σyk=vctg0σλk给出，这种假设不失一般性。

Kalman 滤波方程的形式仍与文献［4］182一致，如下

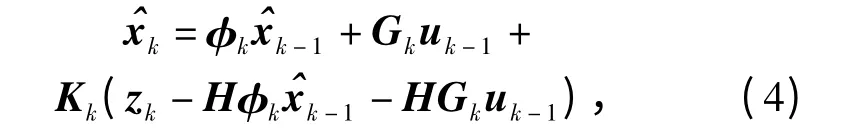
其中，Kk为增益矩阵，由递推矩阵方程计算

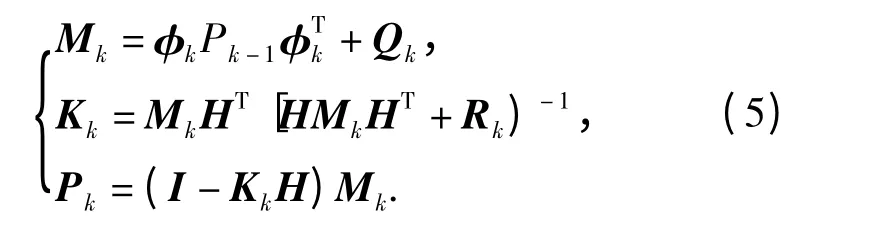
Pk代表更新前的状态估计误差，Mk代表更新后的状态估计误差，Qk为离散过程噪声矩阵。

2 最优制导精度仿真

间瞄寻的导弹末制导方式为电视或红外成像主动导引，识别低空直升机目标距离大于2 km，识别目标后进入末制导，要求脱靶量≤1 m，末制导最大飞行时间tmax=10 s 左右。

Kalman 滤波器应用于最优制导寻的回路，前提条件是已知导引头量测噪声及目标机动统计特性。导引头量测噪声由导引头及弹上测量器件的精度决定，对于特定的产品为一固定值，此处为σλ=0.001 rad.

对于直升机目标的机动统计特性，由于直升机动力性能和驾驶员生理条件的限制，其机动强度有一个限度。此处假设其最大机动加速度atmax=10 m/s2(1 g 左右)，发生概率Pmax=0.1;非机动发生概率P0=0.5;机动时间常数的倒数αt=0.1，计算得σ2t=30 m/s2.

末制导初始条件为:导弹速度为vm0=200 m/s，导引头初始指向角为ε0=5°=0.087 3 rad，直升机目标初速为vt0=30 m/s，与弹目线呈αt0=0°角相向行驶，因此弹目相对速度vc=230 m/s.

tg0的初始估计值为末制导最大飞行时间tmax，实际仿真中，利用上一次得到的tg0减去采样间隔作为本次tg0的值。

初始状态估计确定为

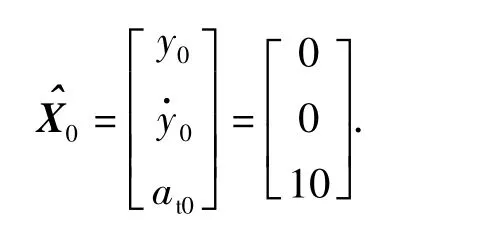
初始估计误差协方差阵确定为

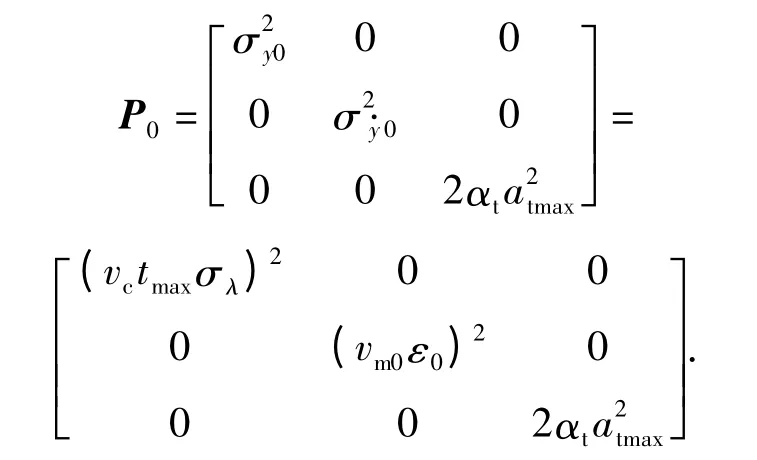
初始估计误差P0的确定不是唯一的，但仿真表明以上取值对状态估计的收敛速度有较好贡献。

Kalman 滤波采样步长设为ts=0.1 s.

仿真计算时，由于暂无导引头测量值，测量值用最优制导计算的理论值叠加白噪声来表示，理论值在Kalman 滤波采样步长内部用龙格库达方法迭代计算，计算步长为0.01，叠加的白噪声来自量测噪声σλ=0.001 rad;因此最优制导仿真的外层是步长为0.1 s 的Kalman 滤波迭代，内层是步长为0.01 s龙格库达迭代。

用以上条件进行100 次的蒙特卡罗最优制导仿真，得出每个时刻的系统状态估计，从而获知导弹脱靶量均值、目标加速度、导弹加速度等指标，见图1、图2和图3.

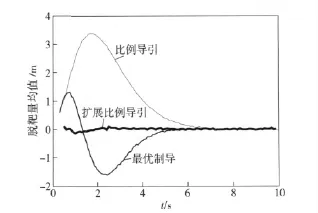
图1 3 种导引律的脱靶量均值比较Fig.1 Mean of three guidance law’s miss distance

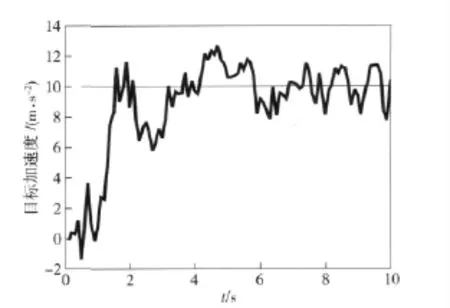
图2 Kalman 滤波预测的直升机目标加速度Fig.2 Helicopter acceleration forecasted by Kalman filter

图1表明，在考虑导弹惯性滞后以及目标机动的情况下，对于间瞄寻的导弹，当采用比例导引和扩展比例导引时，只有当末制导时间大于4 s 时，才能达到要求的制导精度。

若是采用比例导引，当末制导时间小于4 s 时(这时大约离目标还有800 m 左右)，脱靶量将大于1 m，不能满足指标要求。因此，该导弹必须在距离目标800 m 之前就由中段制导转入末端制导，才有可能有效命中直升机目标。

若是采用扩展比例导引，当末制导时间小于3.2 s(这时大约离目标还有640 m 左右)，脱靶量大于1 m，不满足指标要求。因此，该导弹必需在距离目标640 m 之前就由中段制导转入末端制导，才有可能命中直升机目标。从图3可以看出，如果末制导时间足够，扩展比例导引对导弹的加速度需求低于比例导引。

图2表明，Kalman 滤波对直升机机动的预测在实际的直升机机动值左右波动，2 s 后对直升机加速度估值误差稳定下来，并达到较高精度。

图3表明，利用预测的直升机加速度，最优制导所需的导弹加速度很小，并能够使导弹在末制导时间0.5～10 s 范围内接近零脱靶量，这对于人在回路的间瞄寻的导弹非常有用处，可使地面射手利用导弹导引头回传的战场图像背景充分识别目标，从容控制导弹由中制导转入末制导，确保有效摧毁直升机这样的高机动目标。

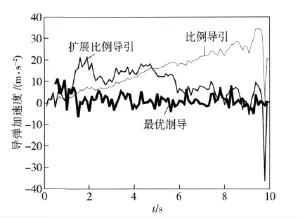
图3 三种导引律所需的导弹加速度比较Fig.3 Missile acceleration needed by the three guidance law

3 结论

本文建立了最优制导的Kalman 滤波模型和测量模型，提出了估计目标机动加速度信息的计算方法。结合数学模型，利用一个间瞄寻的导弹的性能参数，进行了数字仿真，结果表明，目标机动估计应用于最优制导律的方法可行，与纯比例导引比较，有可能在不增加弹上硬件测量成本的条件下，显著改善该导弹命中机动目标的精度。

References)

［1］ 钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京:北京理工大学出版社，2000.QIAN Xing-fang，LIN Rui-xiong，ZHAO Ya-nan.Missile flight dynamics［M］.Beijin:Beijing Institute of Technology Press，2000.(in Chinese)

［2］ 李小兵，刘兴堂.对付大机动目标的扩展比例导引律研究［J］.空军工程大学学报，2001，2(3):1-4.LI Xiao-bing，LIU Xing-tang.Study on generalized proportional navigation for coping with intercepting high maneuvering targets［J］.Journal of Air Force Engineering University，2001，2(3):1-4.(in Chinese)

［3］ Qiao X D，Wang B S.A Motion model for tracking highly maneuvering targets［J］.IEEE，Transaction on AES，2002.

［4］ Paul Zarchan.Tactical and strategic missile guidance［M］.Second Edition.Washington，DC:American Institute of Aeronautics and Astronautics，Inc，1994.

［5］ 郑友祥.战场运动目标参数估计与预测［J］.战术导弹技术，2010，(4):52-56.ZHENG You-xiang.Estimation and prediction of moving parameter of battlefield target［J］.Tactical Missile Technology，2010，(4):52-56.(in Chinese)

［6］ 连葆华，崔平远，崔祜涛.一种改进的最优制导律及其仿真研究［J］.飞行力学，2001，19(3):36-40.LIAN Bao-hua，CUI Ping-yuan，CUI Hu-tao.An improved optimal guidance law and its simulation study［J］.Flight Dynamics，2001，19(3):36-40.(in Chinese)

［7］ 周启煌，单东升.坦克火力控制系统［M］.北京:国防工业出版社，2003.ZHOU Qi-huang，SHAN Dong-sheng.Tank fire control system［M］.Beijing:National Defense Industry Press，2003.(in Chinese)