不确定网络控制系统保成本观测器设计

孙连坤，万振凯，张桂玲

(天津工业大学 计算机科学与软件学院，天津300160)

0 引言

1999年Walsh 教授综合前人的研究成果，正式提出了目前被大家广为接受的网络控制系统(Networked Control Systems，NCSs)概念［1］。与传统的点对点结构的系统相比，NCSs 具有资源共享、远程操作和控制，提高系统的诊断能力、方便安装与维护，增加系统的灵活性和可靠性的特点。

目前对NCSs 的研究，大多是针对线性时不变对象的。文献［2］考虑了网络时延因素的影响，并基于此来自适应调节PI 控制器的增益参数。文献［3］研究了信息传输前进行预处理的问题，通过智能传感器计算一个本地的最优估计值，再运用Kalman 滤波器对该值进行处理。文献［4］研究了具有随机时变延时的NCSs 的H∞控制问题，设计了基于观测器的输出反馈控制律。文献［5］分别运用扩展Kalman 滤波与变尺度估计的方法对非线性被控对象的NCSs 进行状态估计，得到保证估计误差协方差有界的充分条件。文献［6］运用最优估计的方法分析了具有随机时延与丢包的NCSs，得到不依赖于时延与丢包的估计器。上述研究通常只针对单一的网络因素影响，并且假设网络能够提供足够的带宽。但在实际应用中，单一考虑时延或丢包并不能全面反映网络影响;此外，由于时变的网络流量和未知扰动，网络并不总是能提供系统设计时所需带宽。

为此本文将网络当前的综合服务质量作为参考量，在不确定NCSs 的框架下设计一种SOD 调度策略，传感器端将根据输出信息的重要程度对数据进行处理，从而减少非重要信息对网络资源的占用，以达到降低网络需求的目的。在此基础上，考虑输出反馈情况，设计保成本观测器，使得观测误差不超过一个上界。

1 系统描述

本文研究的网络控制系统结构如图1所示，通过添加一个QoS 估计器可以实时获取网络性能，并以此作为SOD 调度策略的依据。例如:假设SOD调度策略所确定的阈值为Δ(t)，它将与网络QoS 存在如下函数关系

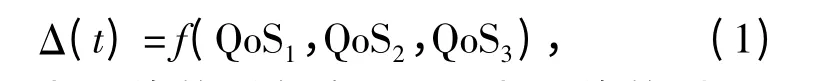
其中:QoS1为网络的丢包率;QoS2为网络的时延;QoS3为网络的吞吐量，这也是网络QoS 中最主要的3 个性能指标。Δ(t)随着网络的QoS 实时变化，但其上、下界是可以确定的，上述描述在分布式NCSs中是可以实现的［7］。在SOD 调度策略的作用下，传感器只传输重要数据，即当新的数据变化大于一定值的时候才作处理。

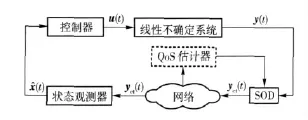
图1 线性时变不确定对象的NCSs 结构图Fig.1 Structure of NCSs with linear time-varyinguncertain plant

考虑如下线性不确定系统

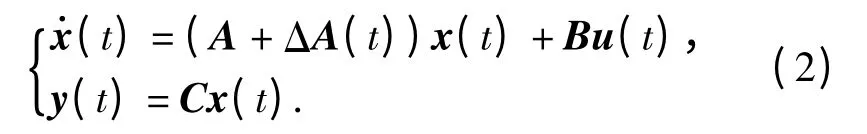
其中:x(k)∈n为系统的状态向量;u(k)∈m为系统的控制输入;y(k)∈p为系统的观测输出。A，B，C 是具有相应维数的定常矩阵。ΔA(t)是具有适当维数的，表示系统不确定性的时变矩阵，满足以下形式

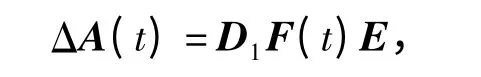
其中:D1∈n×r;E∈l×n是已知的定常矩阵;F(t)∈r×l为不确定函数矩阵，并属于如下集合{F(t)|F(t)TF(t)≤I，∀t}.

1.1 SOD 调度策略基本思想

由于网络通信约束的限制，传感器不可能将每次采集的信息均成功传输，尤其在无人飞行器、无线传感网络中，由于装置的能量限制，使得传感器尽可能只传输重要信息以减少能量损耗。传统的基于时间的周期采样调度策略，不能很好地解决上述问题，主要原因在于周期采样只关注信息处理的快慢，其周期选取是基于系统最坏情况的，一经选定就不能根据信号变化动态调整。

SOD 调度策略属于基于事件的采样，相比等时间间隔采样，其只对超过一定阈值的信息进行处理，发送原则如图2所示，阈值可以提前设定或实时在线调整，其体现了当前传输信息的重要程度。它最大的特点是可以减少传感器节点的平均数据产生率，这对于突发信号尤其有效。

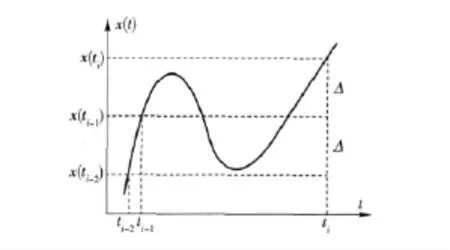
图2 SOD 发送原则Fig.2 Send principles of SOD

本文采用的SOD 调度策略是一种复合采样架构，即首先在本地对连续信号进行周期采样，这样能保证对初始信号进行有效的跟踪;随后再根据SOD采样调度策略进行数据处理与发送，这里我们假定阈值Δ(t)随着网络QOS 的变化而变化，但其上、下界Δmax、Δmin已知，在其作用下传感器节点的平均数据产生率也将动态变化，以此达到减少数据发送、节约带宽的目的。

实际应用中系统可基于特定的QoS，依据公式(1)计算出阈值Δ(t)的变化范围，建立阈值表。QOS 估计器按一定周期向网络发送探测包，在线获取网络服务质量，即网络时延、网络丢包率、网络吞吐量，并通过查表或查值技术得到一定网络服务质量下的具体的SOD 采样调度策略。

1.2 基于SOD 调度策略的系统模型建立

当采样周期远小于被控对象的主导时间常数时，系统可视为连续系统［8］。此外，由于NCSs 中任何网络介质都有其固有的网络服务质量，即网络时延上限、网络丢包上限、网络吞吐量上限等，从这个意义上说，网络的影响是有界的。基于上述考虑，本文假设网络的影响可视为有界连续函数φ(t).在这种情况下，进行网络观测器设计的关键是要将网络环节转化为系统的不确定块。

在［ti，ti+1)内，由QOS 确定的阈值为Δ(ti)，系统最后一次的输出值为y(ti)，实际用于观测计算的系统输出为yct(t)，如图3所示。则在下一次数据更新之前，有如下关系式

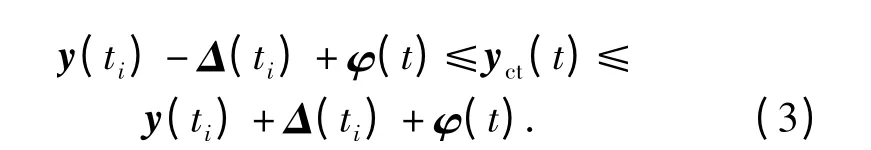
图3 基于SOD 的被控对象Fig.3 The controlled plant based on SOD

由式(3)可得

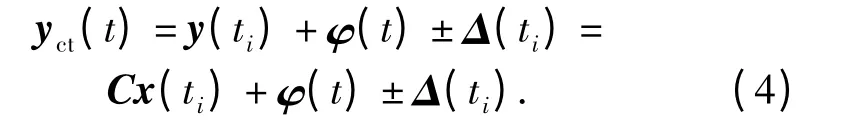
假设‖Δ(t)‖≤α，其中α 为确定常数，‖φ(t)‖≤β，其中β 为确定常数。为了将调度策略的影响建模到系统中，定义Ξ(t)=φ(t)±Δ(t)，假设ΔC(t)·x(t)=Ξ(t)，满足ΔC(t)=D2F(t)E，这里D2∈是已知的定常矩阵，F(t)∈r×l为不确定函数矩阵，并属于如下集合:

Ω={F(t)|F(t)TF(t)≤I，∀t}.

则考虑SOD 调度策略后的线性不确定NCSs 有如下形式

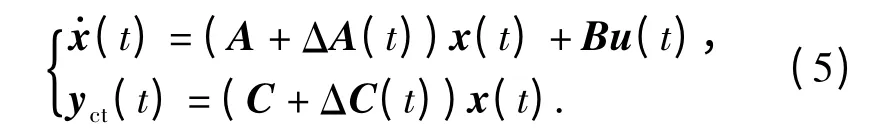
由上述分析可知，在考虑SOD 调度策略后，系统由式(2)转化为式(5)，SOD 调度策略以及网络的影响主要体现在系统的输出添加了额外的时变不确定项。

2 不确定NCSs 的保成本观测器设计

在许多实际问题中，系统的状态往往不能直接测量，需要进行观测器的设计。本文中由于不确定参数的变化及Δ 值的调整，要求观测器具有良好的鲁棒稳定性，此外，还应保证其它适当的性能指标，如估计误差的界限等。利用保成本观测器是解决这一问题的有效方法之一［9］。

考虑SOD 调度策略后的线性不确定NCSs(令u(t)=0)

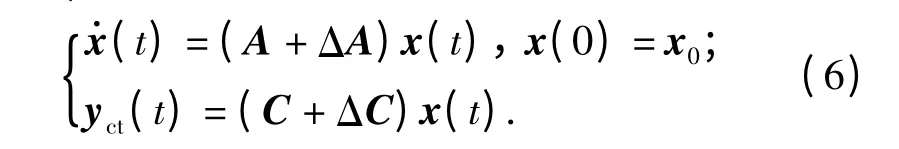
x0为初始条件，且假设为零均值高斯随机向量。

假设1:系统(6)为二次稳定的，即存在一个对称正定矩阵P，满足(A+ΔA)TP+P(A+ΔA)＜0.

考虑如下形式的观测器:

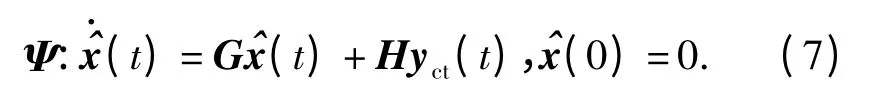
表示观测误差输出，其中L 为已知定值矩阵，则由式(6)、式(7)可得增广系统为

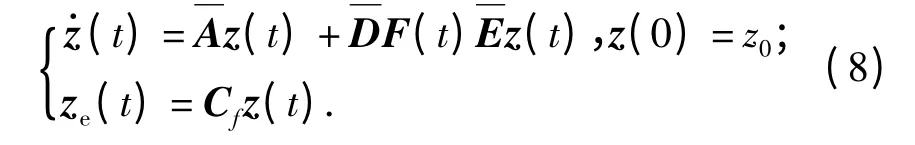
对系统(8)，定义二次型性能指标:

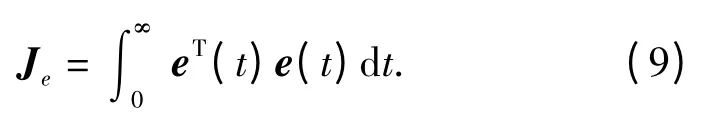
对于保成本观测器，引入如下定义:

定义1［10］:考虑不确定系统(6)和性能指标(9)，若存在观测器(7)和一个正数J*e，使得对于所有不确定函数矩阵F(t)，增广系统(8)是二次稳定的，且满足Je≤J*e，则J*e称为保成本，观测器(7)为保成本观测器。

根据上述定义，接下来要确定观测器参数G，H，并且证明观测器(7)为不确定系统(6)的保成本观测器。

2.1 保成本观测器的存在条件

定理1:对不确定系统(6)和性能指标(9)，如果对称正定矩阵使得对于所有不确定函数矩阵F(t)，满足:

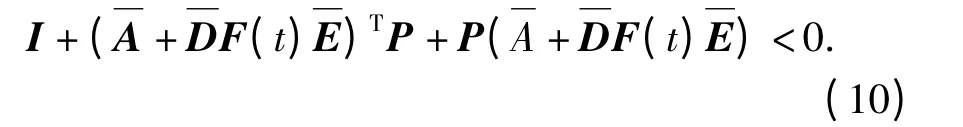
则观测器(7)为不确定系统(6)的一个保成本观测器，且此时观测误差成本上界=L* Trace(P22)*LT，P22为成本矩阵。

证明 选取Lyapunov 函数V(t)=zT(t)Pz(t)，由矩阵P 的正定性可知Lyapunov 函数V(t)是正定的。则沿系统(8)的任意轨线，V(t)关于时间的导数根据条件(10)，对于所有不确定函数矩阵F(t)，

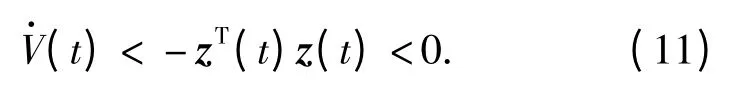
由Lyapunov 稳定性理论，增广系统(8)二次稳定。

进一步，式(11)两边对时间t 从0 到∞积分，可得

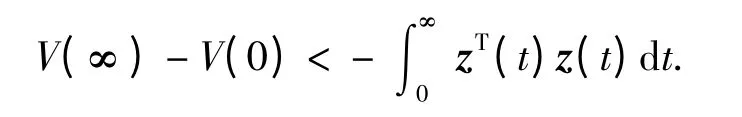
由于增广系统(8)二次稳定，所以V(∞)→0，因此有

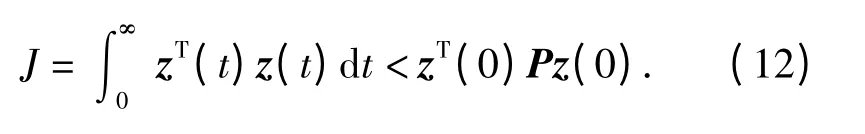
J=E［J］＜E［zT(0)Pz(0)］=Trace(P).

进而有:

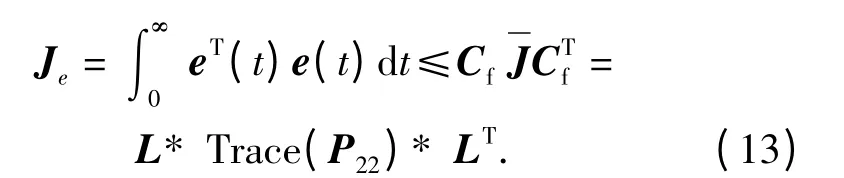
根据定义1 可得，J*e=L* Trace(P22)* LT是相应的增广系统(8)的观测误差成本上界。定理得证。

定理1 给出了不确定系统(6)保成本观测器存在的充分条件，但其验证条件包含了不确定矩阵F(t)，因此要验证对于所有允许的不确定F(t)，不等式(10)都成立仍然是一件困难的工作。接下来将运用LMI 给出这一条件的等价刻画。

2.2 保成本观测器设计

引理1［11］(Schur 补定理):设Y，D，E，F(t)为具有适当维数的实矩阵，其中Y=YT，FT(t)F(t)≤I，则Y+DF(t)E+ETFT(t)DT＜0 当且仅当存在标量ε ＞0，使得Y+εDDT+ε-1ETE ＜0 成立

引理2［12］(正交补定理):给定矩阵Γ，Λ，Θ，则ΓXΛ+(ΓXΛ)T+Θ ＜0 关于X 有解的充分必要条件是:Γ⊥ΘΓ⊥T＜0，ΛT⊥ΘΛT⊥T＜0 式中Γ⊥，Λ⊥分别表示Γ，Λ 的正交补，即Γ⊥Γ=0，Λ⊥Λ=0.

定理2:考虑具有SOD 调度策略的NCSs(6)和观测器Ψ，使得对于所有不确定函数矩阵F(t)，满足条件(10)的充分条件是存在标量ε ＞0，矩阵Q12∈n×n，对称正定阵X1，Q2，Ω，L∈n×n，使得下列不等式同时成立:

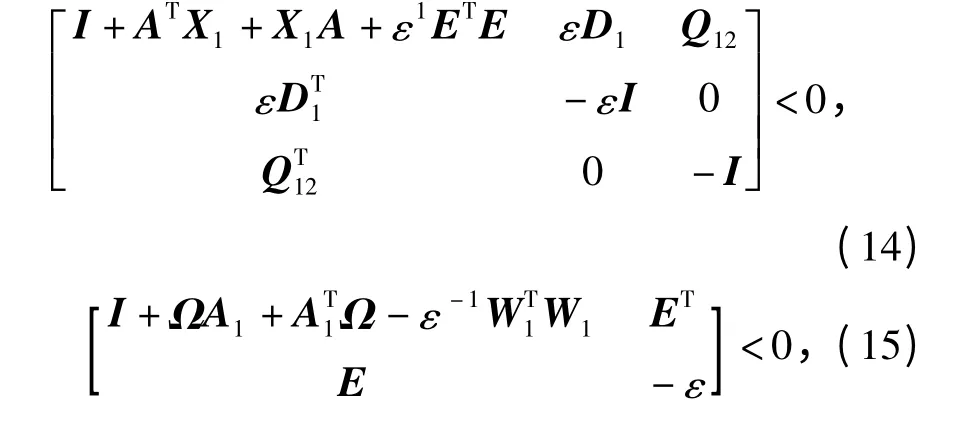
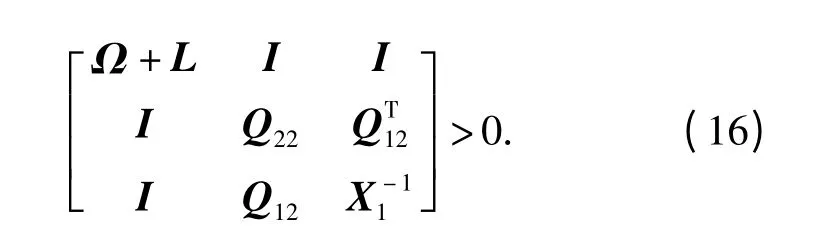
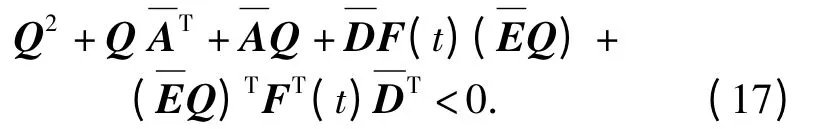
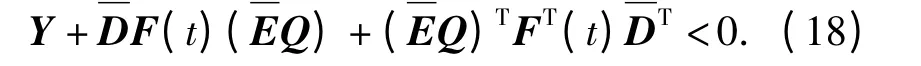
根据引理1，上述矩阵不等式对于所有不确定函数矩阵F(t)成立，当且仅当存在标量ε ＞0，使得

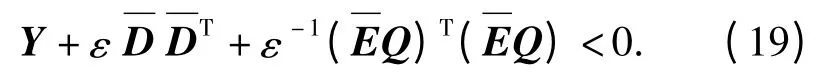
进一步将式(8)中的系数矩阵代入上式可得

式中:

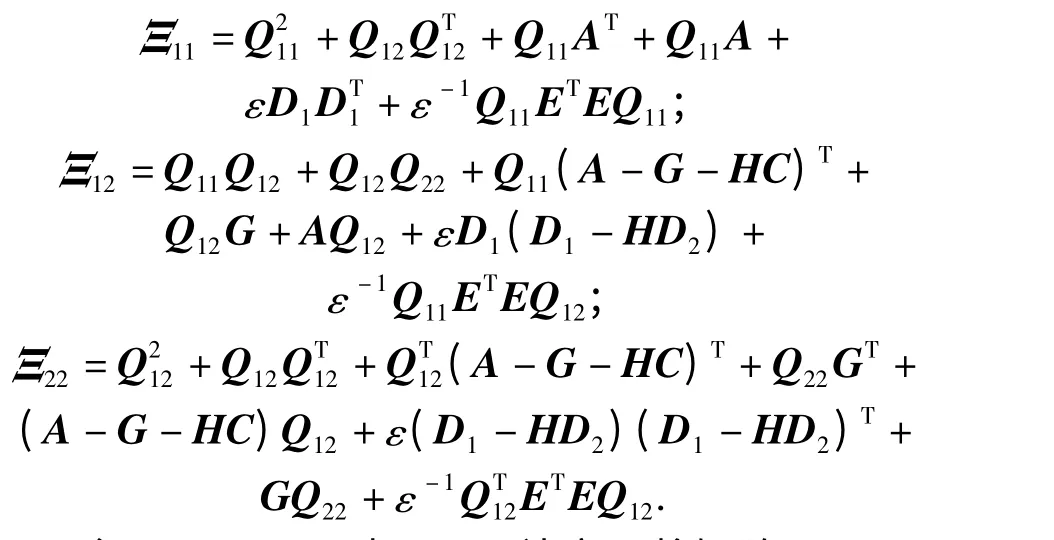
令G1=A-G，由Schur 补定理将矩阵Φ 展开，并将其分为两部分:一部分不含G1，H 的矩阵A#;另一部分为含有G1，H 的矩阵A*，即

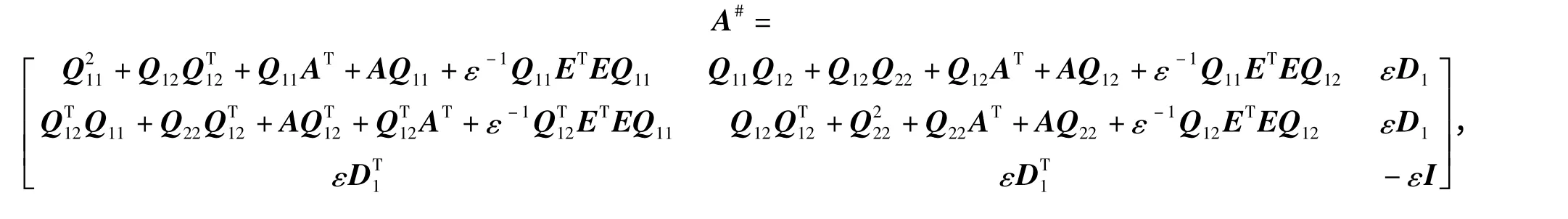
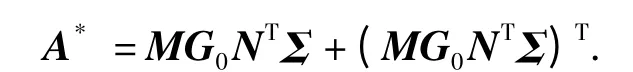
式中:M=［0 I 0］T;G0=［G1-H］;

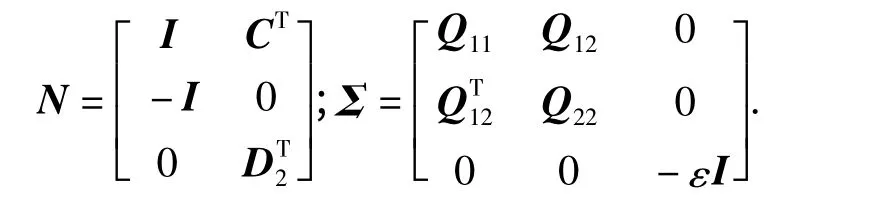
此时式(20)转化为

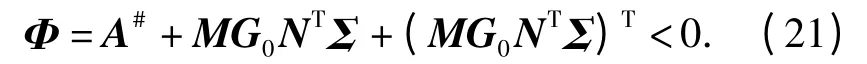
由引理2 可知，式(21)关于G0有解的充分必要条件是:

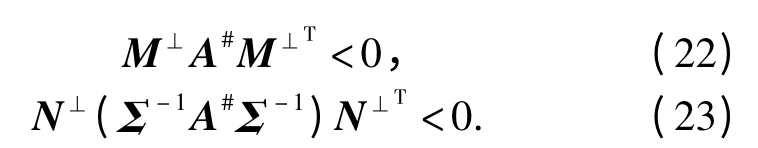
为明细式(22)、式(23)，接下来分3 步证明它等价于式(14)-式(16).

进一步由Schur 补定理可得

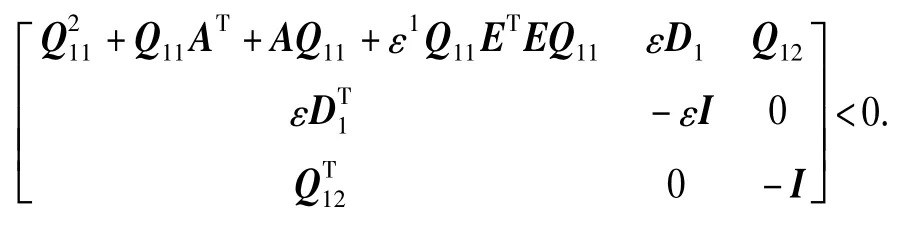
上式分别左乘、右乘diag(Q-111I I)，且令X1=由Schur 补定理可得

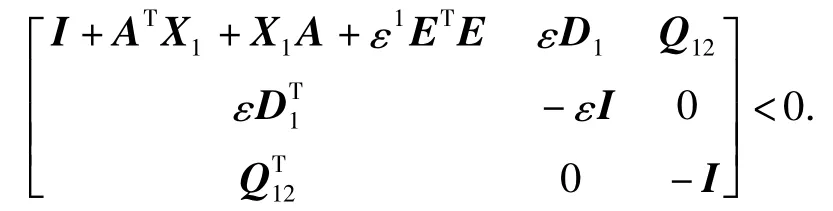
即为式(14).

所以将Σ-1，N⊥代入(23)，同时令A1=A+D1W1，Ω=P11+P12+PT12+P22，并运用Schur 补定理可得

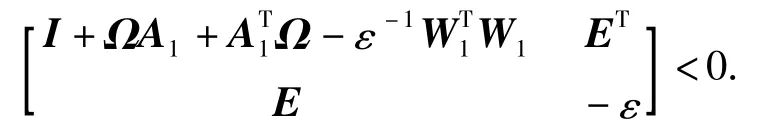
即为式(15).

步骤3 为求出P22的值，首先需要求Q22，将Ω展开为

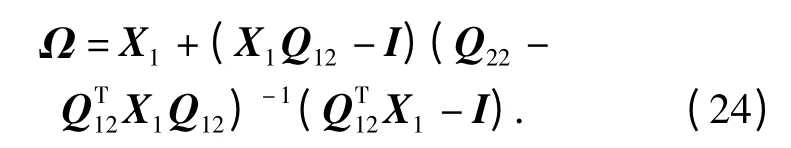
上式成立的充分必要条件是存在正定对称矩阵L∈n×n使得:

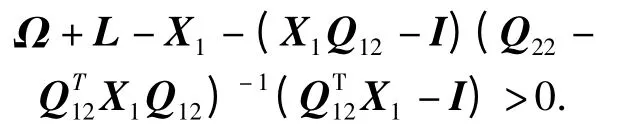
由Schur 补定理可得

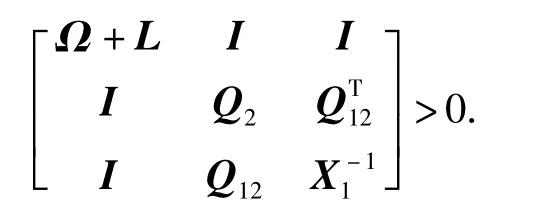
即为式(16).

利用现有的Matlab 仿真环境中LMI 工具箱可求解出式(21)中的G1，H，进而由G1=A-G 求出G，从而确定了保成本观测器的参数。通过求解矩阵不等式(14)-式(16)，可求得Q，进而由P-1=Q，可以确定P.

定理2 表明系统(6)的保成本观测器存在，且保成本矩阵为P22.显然，若保成本观测器存在，如何进一步优化保成本矩阵P22是很有意义的。因为P22正定，如果极小化Trace(P22)，那么在一定程度上就优化了P22，所以我们给出Trace(P22)的优化方法。

定理3 若以下优化问题

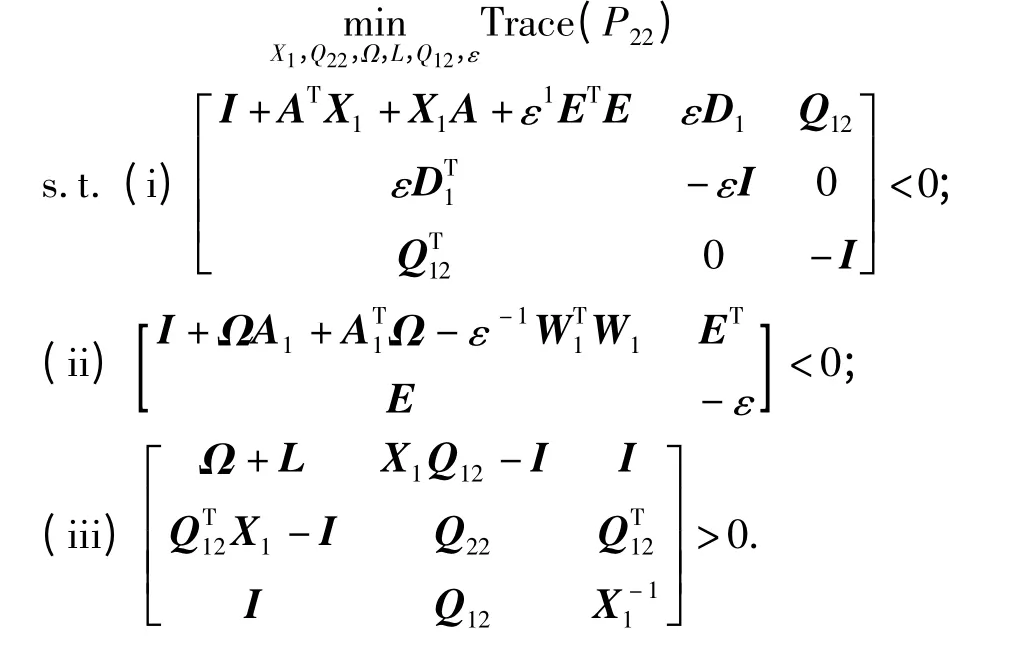
有解X1，Q2，Ω，L，Q12及ε ＞0，则Ψ 为最优状态保成本观测器，且可保证系统(6)的成本最小。

证明:由定理2 可知Ψ 是由X1，Q2，Ω，L，Q12及ε ＞0，确定的保成本观测器，不难发现只有P22的对角线才有估计误差的真正信息。因此对P22的迹进行优化，也就是使估计误差达到最小，从而获得最优保成本观测器。结论得证。

3 仿真

考虑如下线性不确定系统

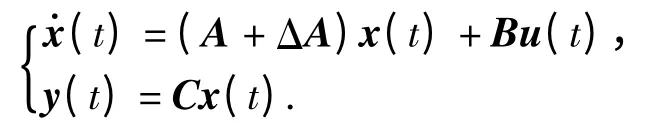
性能函数

其中:R1=R2=I，给定初始性能上界J*=3.

使用Matlab 仿真环境中Truetime 工具箱建立相应网络环境，针对加入SOD 调度策略后的线性不确定NCSs，根据1.1 小节的描述可以确定，‖φ(t)‖≤

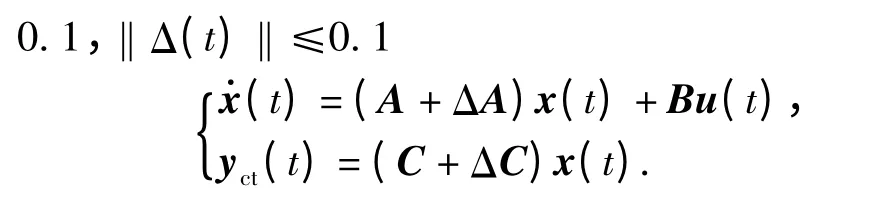
保成本观测器方程:

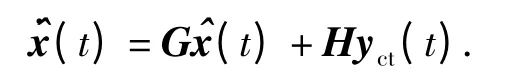
由定理2 通过Matlab 的LMI 工具箱求解观测器矩阵可得:

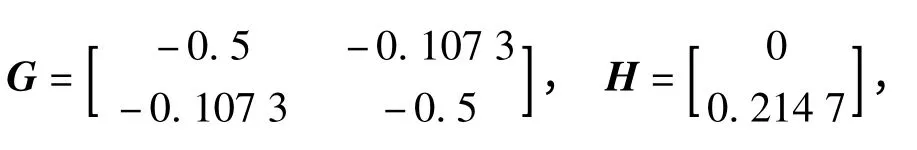
性能指标上界J*=2.347 5 ＜3.

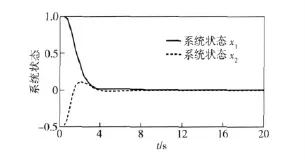
图4 具有SOD 调度策略的NSCs 状态Fig.4 The states of NCSs with SOD scheduling strategy

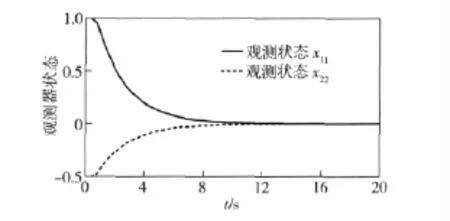
图5 具有SOD 调度策略的NSCs 观测器状态Fig.5 The observer states of NCSs with SOD scheduling strategy

图4、图5中:x11 为状态x1 的观测值;x22 为状态x2 的观测值。仿真结果表明，本文设计的保成本观测器在保证给定性能的前提下，能较好的跟随系统状态。

4 结束语

本文研究了具有通信约束的网络控制系统保成本观测器设计问题。介绍了SOD 调度策略的基本思想，进一步将调度策略和网络影响建立到系统模型中。在此基础上，给出了系统保成本观测器存在的充分条件，利用LMI 和正交补的方法给出了这一条件的等价刻画，并求解了观测器参数，优化了成本矩阵。仿真结果表明本方法的有效性。

References)

［1］ Walsh G C，Ye H，Bushnell L.Stability analysis of networked control systems［C］∥Proceedings of the American Control Conference，San Diego，1999:2876-2880.

［2］ Tipsuwan Y，Chow M Y.On the gain scheduling for networked PI control over IP network［J］.IEEE Transactions on Mechatronics，2004，9(3):491-498.

［3］ Xu Y，Hespanha J P.Estimation under uncontrolled and controlled communications in networked control systems［C］∥Proceeding of the 44th Conference on Decision and Control，Seville，2005:842-847.

［4］ 姚秀明，李清华，等.基于状态观测器的网络化控制系统的h∞控制分析［J］.兵工学报，2008，29(7):870-876.YAO Xiu-ming，LI Qing-hua，et al.Robust observer based h∞control for a class of networked control systems［J］.Acta Armamentarii，2008，29(7):870-876.

［5］ Zhipu J，Chih-Kai K.Estimation for nonlinear dynamical systems over packet-dropping networks［C］∥Proceeding of American Control Conference，New York，2007:5037-5042.

［6］ Schenato L.Optimal estimation in networked control systems subject to random delay and packet drop［J］.IEEE Transactions on Automatic Control，2008，53(5):1311-1317.

［7］ Chow M Y，Tipsuwan Y.Gain adaptation of networked DC motor controller based on QOS variation［J］.IEEE Transactions on Industrial Electronics，2003，50:936-943.

［8］ 于之训，陈辉堂，王月娟.基于H∞和μ 综合的闭环网络控制系统的设计［J］.同济大学学报，2001，29(3):307-311.YU Zhi-xun，CHEN Hui-tang，WANGYue-juan.Design of closed loop network control system based on H∞and μ［J］.Journal of Tongji University，2001，29(3):307-311.(in Chinese)

［9］ Fang X，Wang J.Stochastic observer-based guaranteed cost control for networked control systems with packet dropouts［J］.IET Control Theory and Applications，2008，2(11):980-989.

［10］ Peng C.Networked，guaranteed cost control for a class of industrial processes with statedelay［J］.Asia-Pacific Journal of Chemical Engineering，2007，2(6):650-658.

［11］ Huang D，Nguang S K.Robust disturbance attenuation for uncertain networked control systems with random time delays［J］.IET Control Theory and Applications，2008，2(11):1008-1023.

［12］ Heng W，Guang-hong Y.Fault detection observer design for linear discrete-time systems in finite frequency domain［C］∥IEEE Conference on Decision and Control，New Orleans，2007:378-383.