脉冲磁流体发电机的强磁场研究

谢中元，周霖

(北京理工大学爆炸科学与技术国家重点实验室，北京100081)

脉冲磁流体发电机是一种将化学能直接转化为电能的系统的重要组件之一，其基本原理是导电流体高速切割磁场产生霍尔效应［1］。其中，均匀的强磁场是化学能转化为电能的关键，随着磁感应强度的增强能量的转化效率逐渐提高。因此，研究大空间均匀强磁场形成技术对脉冲磁流体发电机的研制具有重要的理论和实用意义。

永磁体聚磁一般通过磁回路设计和磁块的优化排列来实现，其中，Halbach 阵列和旋转定理是2 种有效形式［2］。李希南［3］等基于Halbach 永磁阵列结构提出了一种特殊的永磁体排列方式，在尺寸为75 mm×35 mm×27 mm 的小空间内形成了高磁场，平均磁感应强度达到1.22 T;Leupold［4-5］等基于Halbach 旋转定理将永磁块排列成中空圆柱形磁场，形成了双聚磁回路，在圆柱孔内(气隙)所产生的磁感应强度超过了永磁体的剩磁感应强度;Abele 等［6］提出了一种与旋转定理相似的永磁体设计方法，利用磁体本身的尺寸和磁块充磁方向的约束形成了双聚磁回路，在一定的空间内形成了高磁场。然而，在大尺寸空间下，由于漏磁较大，磁场均匀性较差，仅仅对永磁块进行结构优化不易实现均匀强磁场，因此必须寻求新的方法来提高磁感应强度和磁场均匀度，其中，在磁回路上添加软铁汇聚磁力线的聚磁技术是一种可行的方法［7］。

根据有关工程设计要求，研究在尺寸为104 mm×360 mm×500 mm 的脉冲磁流体发电机工作区域内，采用往磁回路上添加软铁聚磁的双聚磁回路结构设计方法，应用Maxwell 2D/3D 软件，分析各种影响因素对磁感应强度及其均匀性的影响。设计并研制了由永磁块构成的较大空间磁体装置，测试结果表明在大空间内形成了磁感应强度超过1.24 T 的均匀强磁场，该装置是磁流体发电机的重要部件之一。

1 强磁场形成基本原理

强磁场的形成主要是运用永磁体和导磁体特定的排列方式，尽量使更多的磁通量汇集到工作气隙中去，以提高空间磁感应强度，其中，Halbach 阵列和旋转定理是应用较多的2 种方式。本文根据磁流体发电机对发电通道的特性要求，需要在空间尺寸为104 mm ×360 mm ×500 mm 的区域内形成超过1.0 T 的均匀磁场。由于空间区域比较大，容易造成漏磁，采用单磁路结构设计或者简单的Halbach 阵列结构无法达到应用要求，基于此，依据旋转定理采用设计方案如图1所示。

图1中，1 为环铁，材料为A3 钢或者其他导磁较好物质;2 为高矫顽力的铁氧体永磁体;3 为软铁。图中箭头方向为磁块的充磁方向，外形尺寸依据磁流体发电机研制的技术要求确定。图1中磁场形成原理如图2所示，通过将磁块在空间周围定向排布，增加磁通量，并运用软铁将磁力线定向汇聚于有效空间，形成超过永磁材料剩磁Br的均匀强磁场。其中，软铁的运用可降低磁漏，提高磁感应强度和磁场均匀度，从而有利于在大空间内形成均匀的强磁场。

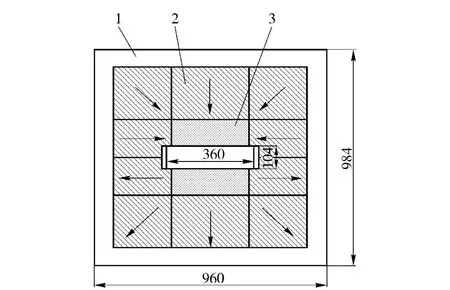
图1 强磁场形成方案图Fig.1 Formulation of strong magnetic field

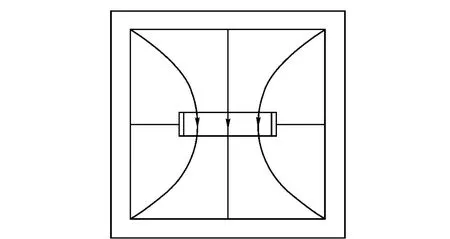
图2 聚磁原理图Fig.2 Sketch of magnet circuit

2 磁感应强度计算及影响因素分析

2.1 磁感应强度计算方法

永磁体的结构设计主要依靠磁体自身的约束形成聚磁，不涉及外部电源，固可直接采用高斯磁通定律［8］进行计算

式中:S 为闭合曲面;B 为磁感应强度。当选定一闭合曲面应用此方程进行计算时，仅能得到该区域内的平均磁感应强度，而磁感应强度的各向分布却无从得知。为了得到磁感应强度沿某一方向的分布规律，需要将(1)式变为微分形式，然后由微分形式导出能用有限元处理永磁体问题的微分方程［9］

2.2 影响因素分析

软铁的有无、软铁的厚度、软铁的材料和磁块材料性质等多方面因素对磁感应强度均有影响，本文借助于Maxwell 2D/3D 有限元软件，通过仿真计算研究磁体系统的优化设计方案。

2.2.1 软铁有无对磁场的影响

采用Maxwell 2D 对含有软铁和不含软铁2 种设计方案进行计算，不含软铁时，相应的空缺部分用磁块补全，仿真模型如图3、图4所示，计算初始条件分别如表1、表2所示，其中外形尺寸以及磁块充磁方向如图1所示，电工纯铁磁特性参数如表3所示，整个磁场按非线性场计算，采用气球边界条件，计算结果如图5～图8所示。

表1 方案1 初始计算条件Tab.1 Initiative calculation conditions of project 1

表2 方案2 初始计算条件Tab.2 Initiative calculation conditions of project 2

表3 电工纯铁磁特性参数Tab.3 Parameter of soft iron

由图5、图6的计算结果可知:采用聚磁技术，2种方案在矩形区域内的磁通密度均得到加强，磁场的均匀性均得到提高;采用含软铁的设计方案时，磁力线汇聚更加明显，磁力线密度较不含软铁设计方案有明显提高。

图3 无软铁计算模型图Fig.3 Calculation model without soft iron

图7、图8为2 种方案在矩形区域内磁感应强度沿x 和y 方向的变化规律，其中，x 方向是指矩形区域内水平方向，y 方向是指矩形区域内垂直方向。由图7、图8可以看出，不含软铁时，矩形区域内能够形成比较高的磁场，平均值达到1.4 T，但是磁场横向波动较大，磁场均匀度为97.5%;含有软铁时，通道中的磁感应强度得到明显加强，平均磁感应强度达到1.7 T，较不含软铁提高21.4%，且磁场均匀度达到99%以上。因此，添加软铁能够提高矩形区域内的磁感应强度和磁场均匀度。

图4 含软铁计算模型图Fig.4 Calculation model with soft iron

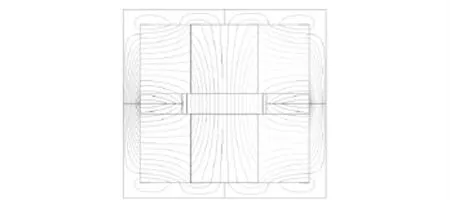
图5 无软铁磁力线Fig.5 Magnetic line without soft iron

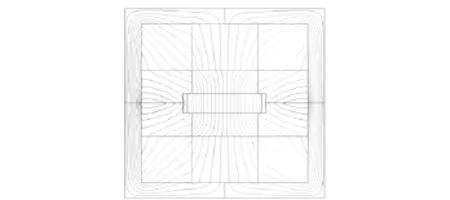
图6 含软铁磁力线Fig.6 Magnetic line with soft iron

2.2.2 软铁厚度对磁场的影响

改变软铁的厚度，研究软铁厚度对有效区域内磁感应强度和磁场均匀度的影响。计算结果如图9～图11所示，其中软铁的厚度变化范围10～200 mm，基本模型如图4所示，其他计算条件同2.2.1 中方案2。

由图9、图10可以看出，不同的软铁厚度对应的磁感应强度在矩形区域内均匀度均比较高，其中，x 轴方向上在-100～100 mm 的范围内，磁感应强度基本不变化，y 轴方向上随着距离的变化磁感应强度基本为一直线。采用聚磁技术后，磁力线在有效空间区域内得到明显加强，提高了磁场均匀度;而随着软铁的加入，磁力线则得到进一步的有效汇聚，磁场均匀度得到进一步提高。

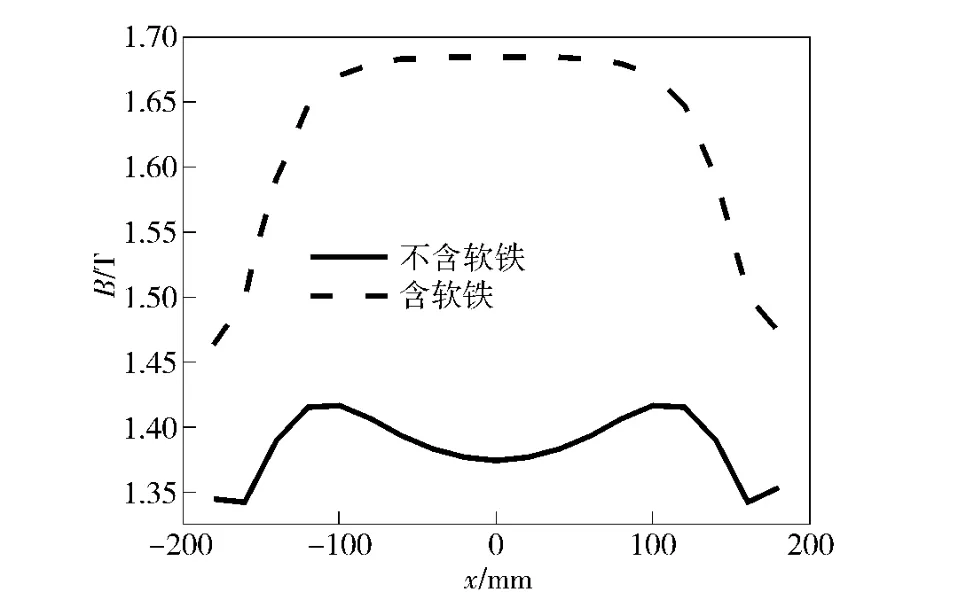
图7 2 种方法磁感应强度沿x 轴方向变化Fig.7 Magnetic flux density along x axis

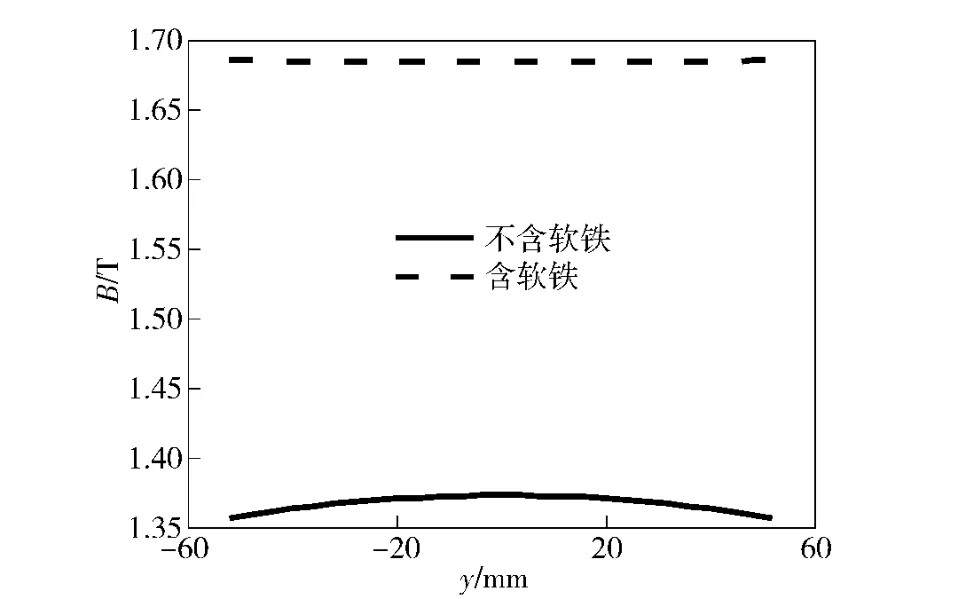
图8 2 种方法磁感应强度沿y 轴方向变化Fig.8 Magnetic flux density distribution along y axis

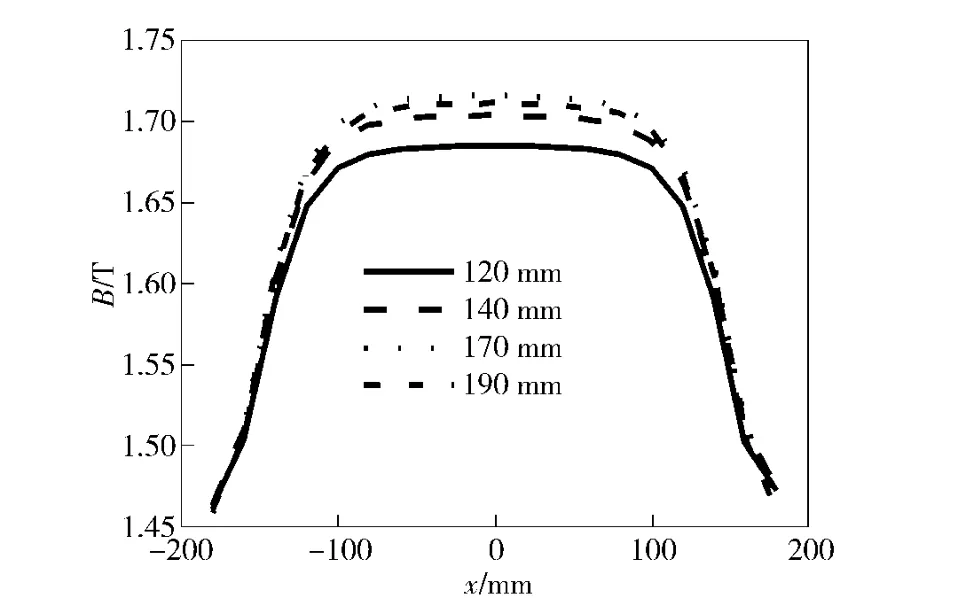
图9 磁场沿x 轴的变化关系Fig.9 Magnetic flux density distribution along x axis

图10 磁场沿y 轴的变化关系Fig.10 Magnetic flux density distribution along y axis

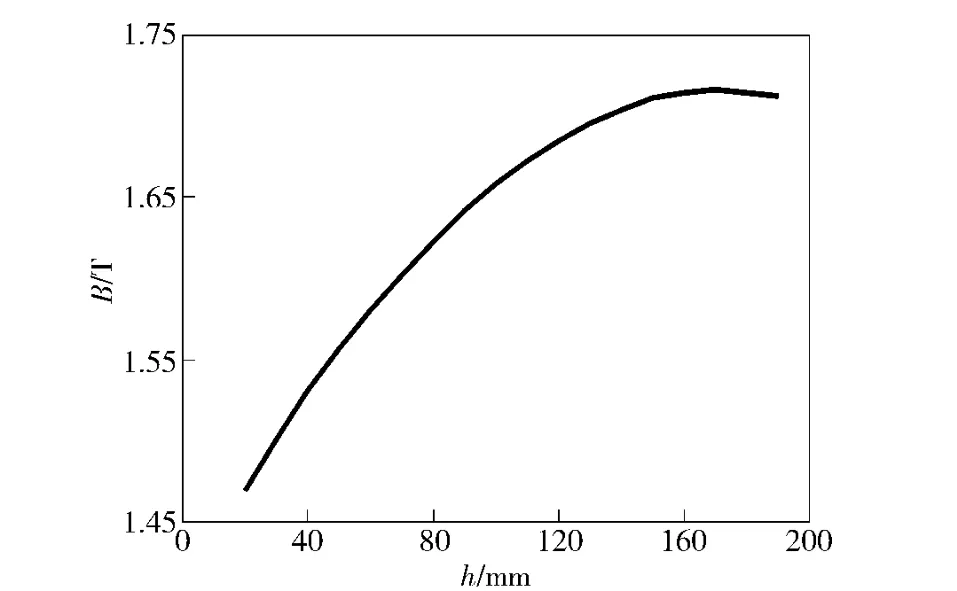
图11 平均磁感应强度随软铁厚度h 的变化关系Fig.11 Changes of average magnetic flux density correlated with thickness h of soft iron

图11为平均磁感应强度随软铁厚度的变化曲线。由图11可知，随着软铁厚度的增加，矩形区域内的平均磁感应强度逐渐加强，当软铁厚度为170 mm 时，磁感应强度达到最大值1.71 T，然后随着软铁厚度的继续增加，磁感应强度开始逐渐下降。其原因在于当软铁厚度较小时，由于磁体的总体尺寸一定，软铁上方的磁块较厚，软铁相对比较薄，磁力线的汇聚不充分，磁漏较大，磁感应强度相对较低;随着软铁厚度的增加，软铁的聚磁效应逐渐得到加强，矩形区域内磁感应强度也随之加强，当软铁厚度为170 mm 时，磁力线充分汇聚，磁感应强度达到最大值;当软铁厚度继续增加时，软铁上方磁块厚度减少的影响逐渐得到显现，磁感应强度开始逐渐下降。

2.2.3 软铁材料对磁场的影响

磁块材料均为M45(钕铁硼永磁体)，软铁材料分别为电工纯铁、1008 钢和1010 钢［9］，计算模型如图4所示，其他计算条件同2.2.1 中方案2。软铁的磁特性曲线，如图12所示，图中H 为磁场强度;磁感应强度随软铁材料的变化关系，如图13所示。

由图13可以看出，软铁材料对磁感应强度有较大影响，其中，1008 钢和1010 钢对磁感应强度有相似的变化规律，且在x 方向磁场均匀度较高，相比之下，电工纯铁的聚磁性能较差，磁感应强度在x 方向产生较大变动。

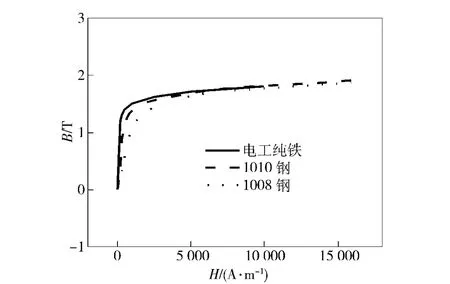
图12 软铁磁特性曲线Fig.12 Magnetic characteristic of soft iron

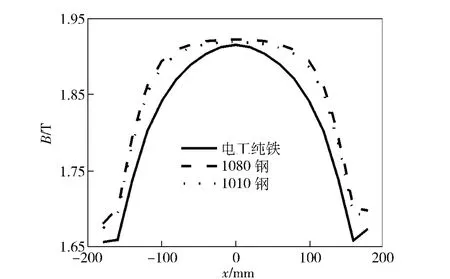
图13 磁感应强度随软铁材料的变化关系Fig.13 Changes of magnetic flux intensity correlated with variation of soft iron material

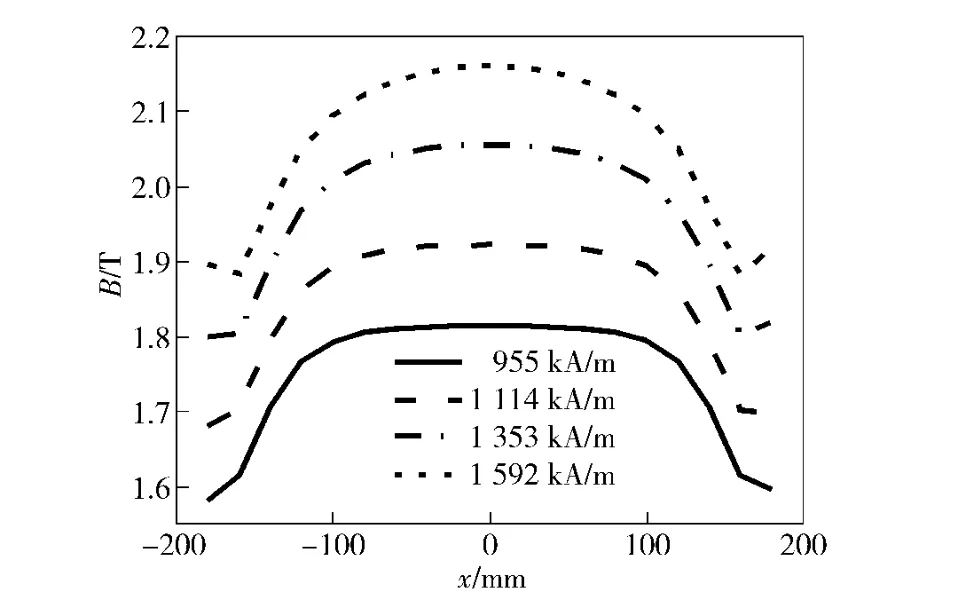
图14 x方向磁感应强度随Hcj的变化关系Fig.14 Magnetic flux intensity distribution along x axis correlated with inner coercive force

图15 y方向磁感应强度随Hcj的变化关系Fig.15 Magnetic flux intensity distribution along y axis correlated with inner coercive force

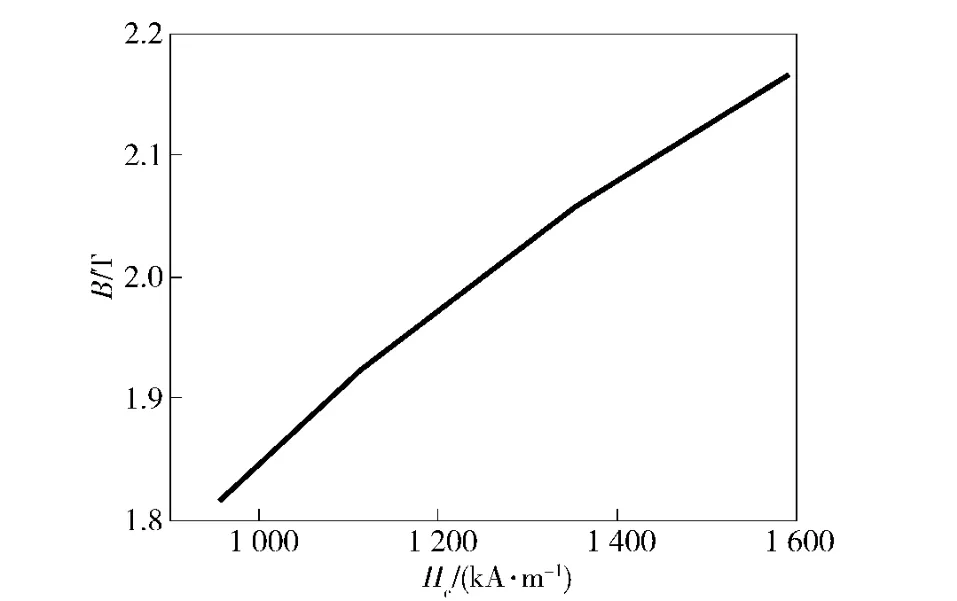
图16 平均磁感应强度随Hcj的变化关系Fig.16 Changes of average magnetic flux intensity correlated with the variation of inner coercive force Hcj

2.2.4 磁块内禀矫顽力(Hcj)对磁感应强度的影响

磁块剩磁均为1.35 T，软铁材料均为1008 钢，Hcj分别在955、1 114、1 353 kA/m 和1 592 kA/m 条件下，研究其对矩形区域内磁场的影响，计算模型如图4所示，其他计算条件同2.2.1 中方案2。计算结果如图14～图16所示。

由图14、图15可以看出，Hcj越高，磁感应强度越高，磁场均匀性越差。当Hcj为1 592 kA/m 时，磁感应强度最大值接近2.15 T，但其在x 方向上明显是中间强两段弱，在y 轴方向上明显是中部弱两端强;当Hcj减少到1 114 kA/m 时，磁感应强度减少到1.925 T，但磁场均匀度得到明显改善，在坐标轴方向上基本不变化。其原因在于:随着Hcj的增加，磁场强度逐渐加强，软铁逐渐达到磁饱和，从而软铁作用逐渐下降，磁场均匀性逐渐降低。

由图16可以看出，随着Hcj的增加，矩形区域内平均磁感应强度逐渐增加，且增加幅度较大。这是由于随着Hcj的增加，永磁体抵抗退磁场的能力逐渐得到加强，因而减少了磁漏，提高了磁感应强度。

2.2.5 环铁厚度对磁场的影响

环铁是组成双磁路通道的重要组成部分，环铁厚度在60～120 mm 范围内逐渐变化，研究环铁厚度对有效空间区域内磁感应强度的影响，内部磁块以及软铁等参数与2.2.1 中方案2 相同，磁感应强度沿x 方向和y 方向的变化如图17、图18 所示。

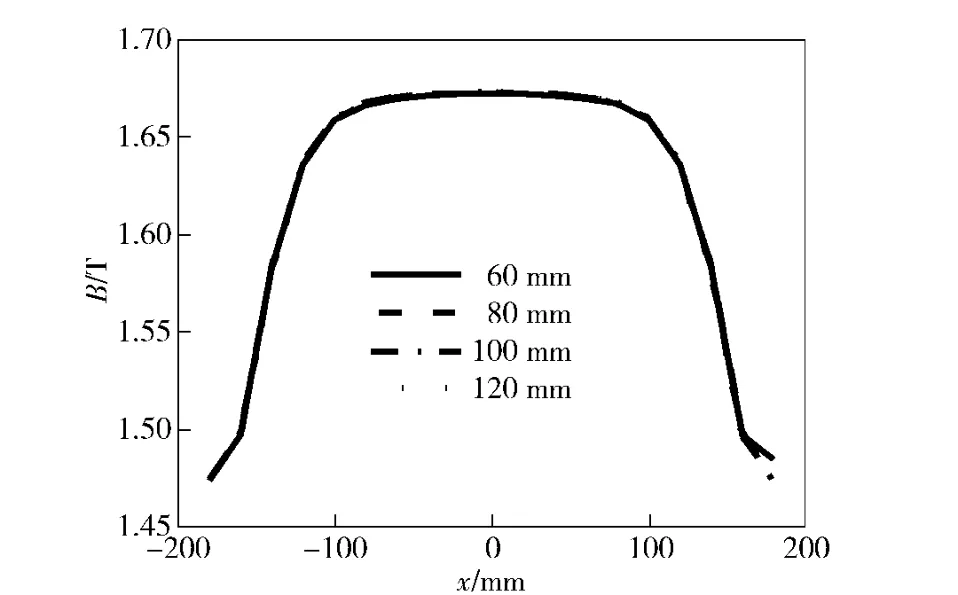
图17 x 方向磁感应强度随环铁厚度的变化关系Fig.17 Magnetic flux intensity distribution along x axis correlated with iron thickness

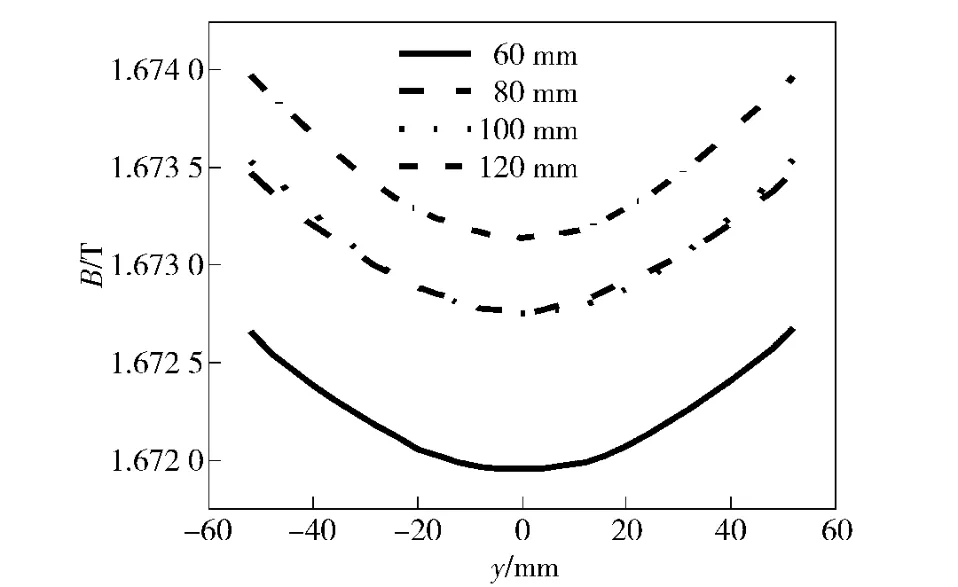
图18 y 方向磁感应强度随环铁厚度的变化关系Fig.18 Magnetic flux intensity distribution along y axis correlated with iron thickness

由图17、图18 可知，环铁厚度对磁感应强度基本不产生影响，x 轴线方向不同环铁厚度形成的磁场基本重合，环铁厚度对磁感应强度影响小。

3 磁体系统方案与样机

3.1 磁体系统方案

根据以上研究结果，选用磁块材料为M45;环铁厚度定为100 mm，材料为A3 钢;软铁选用电工纯铁，厚度为120 mm，外形尺寸如图19 所示，空间尺寸360 mm×104 mm ×500 mm.应用Maxwell 3D 对矩形区域内的磁感应强度进行仿真计算，采用自然边界条件，计算结果如图20 所示。

图20 中x，y 轴含义与上文相同，z 轴方向为有效区域的长度方向，由图可知，磁感应强度沿x、y 和z 轴方向均匀度高，平均磁感应强度达到1.49 T，均匀度达99%.

3.2 磁体系统样机

根据上述方案，对磁流体发电机用磁体进行了加工与装配，装配效果如图21 所示，产品图如22 所示。

图19 三维仿真计算模型Fig.19 Three-dimensional simulation model

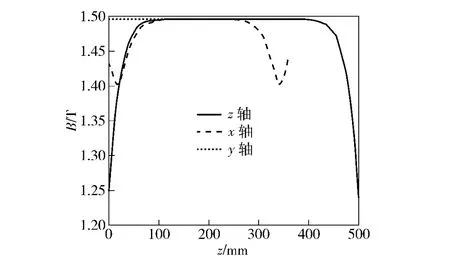
图20 三维仿真计算结果Fig.20 Three-dimensional simulation results

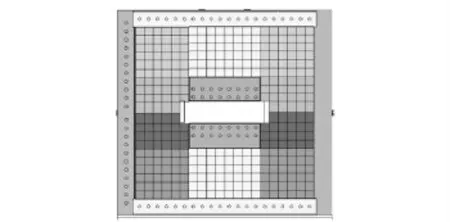
图21 磁体装置工程图Fig.21 Processing map of magnetic facility

图22 磁体装置实物Fig.22 Magnetic facility

采用HV-250 特斯拉计直接对磁感应强度进行测量，测量位置如图23 所示，测试结果如表4所示。

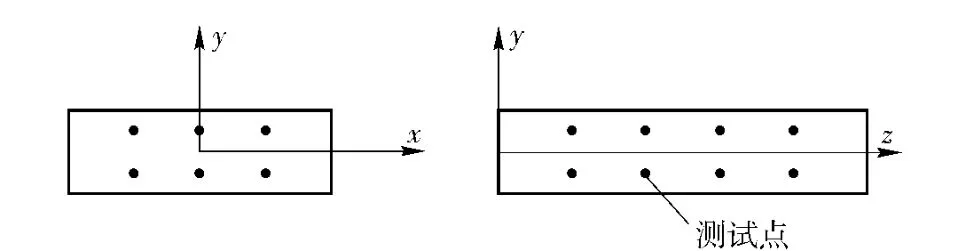
图23 测试点位Fig.23 Test positions

表4中括号内为坐标值，由表中数据可知，平均磁感应强度为1.24 T，矩形区域内磁场均匀度达到95%以上，完全满足设计要求。然而，实测结果较数值计算结果偏低，分析原因在于:在数值计算过程中，磁块与磁块之间不存在空隙，无漏磁，计算属于理想情况，而实际的装配过程中，由于磁体之间存在非常大的排斥力，磁块之间不可避免的会出现间隙，从而出现一定的漏磁，最终导致有效区域内实际磁感应强度较理论计算结果偏小。

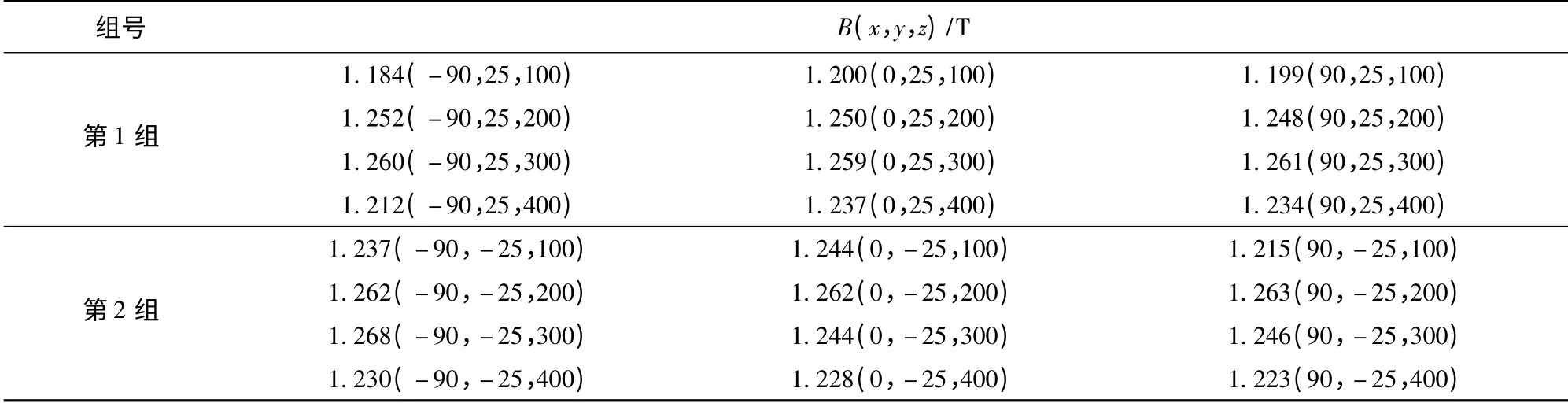
表4 空间内磁感应强度分布Tab.4 Magnetic flux intensity distribution in rectangle area

4 结论

1)软铁的加入能够明显的提高发电通道中的磁感应强度和磁场均匀度，软铁的材料和尺寸对磁感应强度和磁场均匀度具有重要的影响，一定的外形尺寸条件下(960 mm×984 mm×500 mm)，随着软铁厚度的增加，磁感应强度先增加后减少，当磁块材料为NdFe35 时，软铁厚度在170 mm 时磁感应强度取得最大值。

2)在磁体系统外形尺寸一定的条件下，随着磁块内禀矫顽力的增加，有效区域内磁感应强度逐渐增加，磁场均匀度逐渐降低。

3)随着环铁厚度的增加，磁感应强度和均匀度增加幅度很小，环铁厚度对磁感应强度和磁场均匀度的影响可以忽略。

4)当通道空间尺寸为104 mm ×360 mm ×500 mm，对所得到的磁流体发电机磁体优化方案进行了加工制作，发电通道内的平均磁感应强度为1.24 T，磁场均匀度达到95%.

References)

［1］ Naoyuki Kayukawa.Open-cycle magnetohydrodynamic electrical power generation:a review and future perspectives［J］.Progress in Energy and Combustion Science，2004，30:33-60.

［2］ Kumada M，Iwashita Y，Aoki M，et al.The strongest permanent dipole magnet［C］∥Proceedings of the 2003 IEEE Particle Accelerator Conference，Vols 1-5.Portland OR:IEEE，2003:1993-1995.

［3］ 李希南，李春生，严陆光.一种新型双极永磁体的设计与应用研究［J］.电气应用，2007，26(3):60-64.LI Xi-nan，LI Chun-sheng，YANG Lu-guang.Design and application research on dipole permanent magnet［J］.Electrotechnical Application，2007，26(3):60-64.(in Chinese)

［4］ Leupold H A，Potenziani E.Novel high-field permanent-magnet flux sources［J］.IEEE Transactions on Magnetics，1987，23(5):3628-3629.

［5］ Leupold H A，Til A S，Potenziani E.Tapered fields in cylindrical and spherical spaces［J］.IEEE Transactions on Magnetics，1992，28(5):3045-3047.

［6］ Abele M G，Chandra R，Rusinek H，et al.Compensation of nonuniform magnetic properties of components of a yokeless permanent magnet［J］.IEEE Transactions on Magnetics，1989，25(5):3904-3906.

［7］ Dai W，Shen B G，Li D X，et al.Application of high-energy Nd-Fe-B magnets in the magnetic refrigeration［J］.J Magn Magn Mater，2000，218:25-30.

［8］ 高建平.电磁波工程基础［M］.西安:西北工业大学出版社，2008:130-134.GAO Jiang-ping.Base of electromagnetic wave engineering［M］.Xi’an:Northwestern Polytechnical University Press，2008:130-134.(in Chinese)

［9］ 刘国强，赵凌志，蒋继娅.Ansoft 工程电磁场有限元分析［M］.北京:电子工业出版社，2006:1-5.LIUGuo-qiang，ZHAO Ling-zhi，JIANG Ji-ya.Asoft finite element analysis on engineering electromagnetic field［M］.Beijing:Publishing House of Electronics Industry，2006:1-5.(in Chinese)