光学像差图像随机波前编码混合成像

罗林，高晓蓉，王泽勇，王黎

(西南交通大学 光电工程研究所，四川 成都610031)

提高光学系统成像的分辨力水平，一直是光学设计的主要目标，如何减少或消除光学系统像差是光学设计研究领域的重要课题。除了传统的消除像差方法外［1-4］，最近几年，一些作者提出了采用数字图像处理来消除像差对图像分辨率影响的方法［5-9］，Dowski 和Cathey 等［10-12］提出在传统光学系统入瞳处放置特别制作的相位板，对像差或低分辨图像进行波前编码。在采用波前编码的混合光学成像系统中，通过相位板编码物生成的图像，用数字图像处理复原编码图像，所恢复图像的分辨率已达到近光学系统衍射极限水平。

本文提出了一种随机波前编码消除光学像差的方法。采用一种能在光学系统入瞳面上产生随机波前的相位板，使像差图像转变为随机编码图像，该随机相位板不同于Dowski 所提出的，其结构简单、易于加工，对于随机波前并不需要精确设计;用盲反卷积解码中间像成无像差图像。如果这种方法能够成功引入传统光学系统中，就可以选用牺牲一部分仪器加工设计精度，而采用数字图像处理方法最终获得高分辨图像输出，同时可以校正成像过程中的对准误差和减小噪声。

1 随机波前编码成像

随机波前编码成像系统和传统光学成像的区别是在成像系统孔径光阑处放置了一个可产生随机波前的相位板，使具有光学像差的图像受到随机扰动，成为中间像。用位于像面上的数字CCD 采集中间像，并通过数字图像处理解码中间像。相位板在混合光学成像系统中的作用是在光学系统的入瞳面上产生随机波前，从而改变了系统点扩散函数的性质，使中间像对传统光学固定像差的影响不敏感，并通过控制相位屏随机波前特性，使获得的随机扰动中间像更利于数字图像处理算法复原。

按照光学系统非相干成像原理，系统成像特性由点扩散函数表示，也就是

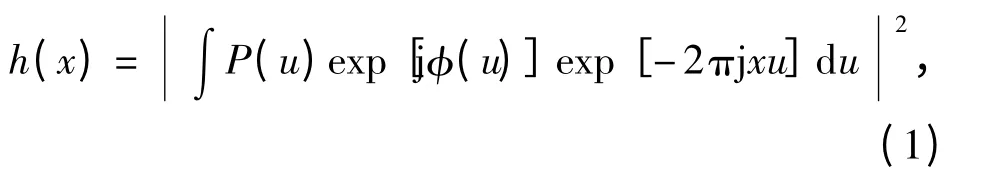
式中:P(u)为理想非相干光学系统光瞳函数;φ(u)为入瞳上的波前相位

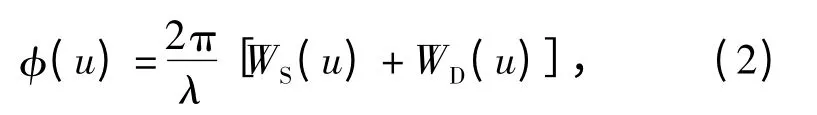
式中:WS(u)为相位板产生的随机像差，WD(u)为光学系统产生的固定像差。

常见的光学系统初级像差的二维形式为［13］

离焦:

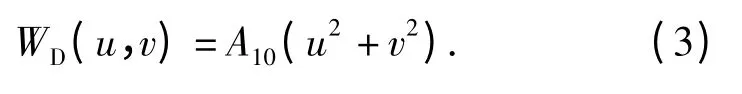
球差:

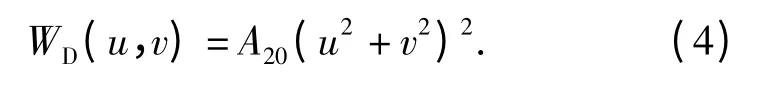
慧差:

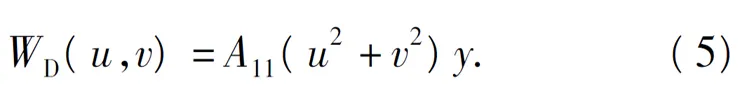
像散:

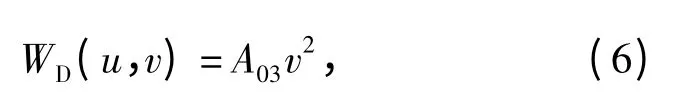
式中Ai为各种像差系数。当波前WD(u，v)=0 时，光学系统为理想成像情况，仪器的分辨率由孔径的衍射效应决定。存在光学像差时，图像的分辨率降低，系统成像特性由(1)式决定，以此评价光学系统的成像质量。当在光学系统入瞳上加入特殊相位板控制其波前，可改变光学系统成像特性。

随机波前编码用特别制作的随机相位板实现，相位板随机波前模型采用［14］

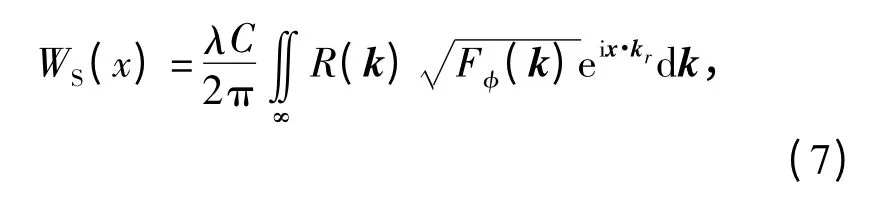
式中:C 为常数;k 为波数;R(k)为0 均值、单位方差的复高斯随机过程;Fφ(k)为具有Kolmogorov 统计分布的相位起伏功率谱

式中r0为相干长度，控制相位板的随机波前特性。

相位板的制作有2 种方法:1)在随机波前编码中，采用特定软件按(7)式生成一组随机波前数据，用微光学加工技术制作已知波前随机特性的相位板;2)采用本文中的激光散斑干涉方法，用全息干板记录散斑干涉图作为相位板。

图1分别表示光学系统在衍射、单独存在离焦像差和在有离焦像差加随机波前扰动情况下的光学系统调制传递函数一维曲线，其中离焦像差最大边缘值为Wm=2λ，经随机波前扰动后，调制传递函数离焦的特征被明显削弱，说明相位板的随机波前扰动可以减小固定像差对图像的影响。

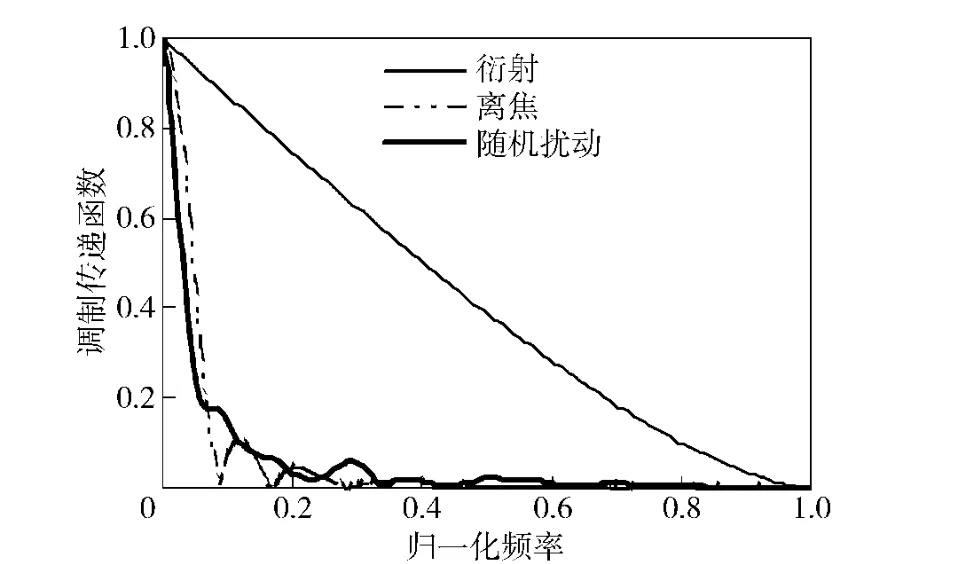
图1 像差为衍射、离焦和离焦加随机扰动情况的光学调制传递函数Fig.1 Optical modulation transfer functions with diffraction or defocuses aberration，and defocus added random wave front

2 波前编码图像解码

经波前编码成像系统后的目标图像是编码退化图像，等于目标函数和系统点扩散函数的卷积，频域表示成

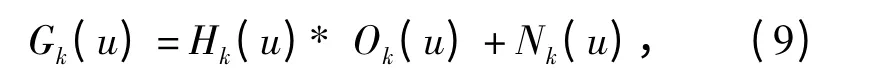
式中:G(u)、H(u)、O(u)、N(u)分别为编码像、点扩散函数、原始目标和噪声的频域表示。

由于未知系统点扩散函数，解码方法采用盲反卷积。在许多场合如天文领域，使用盲反卷积消除大气随机扰动对图像分辨率的影响［15-16］，同样的方法适用于随机波前编码图像的恢复。

假设所有的测量数据都有高斯统计分布形式，每个点扩散函数独立无关。按照Bayes 原则，测量数据、物分布和点扩散函数3 者满足条件联合概率密度

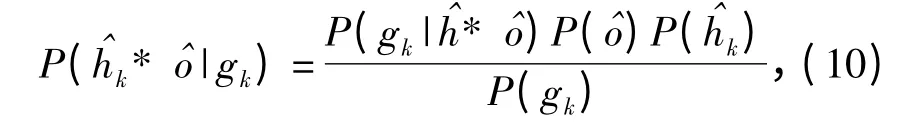
式中P(·)为概率密度函数，优化时采用对数形式的负值作为价值函数即

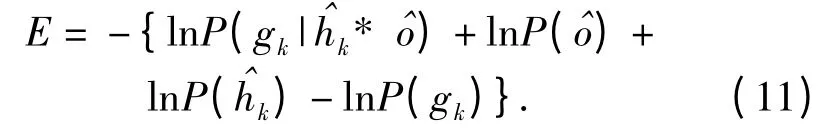
盲反卷积过程通过最小化(11)式和对可能的解进行约束来得到(x)和(x)的估计。式中的第1 项常称之似然项，它形式取决于噪声统计特性;第2、第3 项分别表示有关物分布和点扩散函数的先验知识;第4 项代表测量偏差，如果探测器是无偏的，该项是一常数，优化时可以忽略不计。

考虑到频域中图像的对称性，在频域中实施优化可减少估计的变量数，加快优化速度。不考虑物分布有关的支持域约束，对噪声进行低通滤波，并加入传递函数频率有限带宽约束，则价值函数表示为

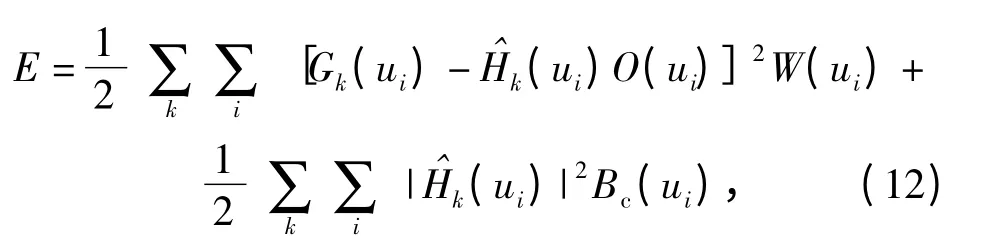
式中:W(u)为低通滤波器，起到抑制噪声的作用;Bc(u)为带通滤波器，作用是限制所估计(x)的频率处于光学系统截止频率uc之内，当u ＜uc时取1，u ＞uc取0.可见，价值函数的优化是一个最小二乘方问题，用共轭梯度优化法进行优化［17］。一个简化的梯度优化迭代算法如下，每一步算法迭代为

式中α 为收敛参数。算法迭代的每一步所得到的估计^hk(x)，^o(x)，均使价值函数减小，因此反复的迭代，并通过给定迭代次数或中止条件，算法最后可得到(x)，(x)的优化估计。算法的收敛性取决于对所估计(x)，(x)施加的约束条件，最简单和最有力的约束是(x)，(x)变量正性化，而点扩散函数归一化则保证优化过程中的能量守恒。调整低通滤波器W(u)的滤波强度，能进一步提高算法的收敛性，对减少恢复图像虚假信息有利。

3 实验模拟结果

为了测试所提出方法的有效性，进行了计算机模拟和实验室实验。在计算机模拟实验时，首先用软件生成一组独立的随机相位数据，模拟相位板，实验室实验则采用激光散斑干涉法制作相位板。

模拟实验像差包括离焦、像散和同时有离焦像散的3 种成像情况，并用256 像素×256 像素的土星作为测试图像。

计算机模拟时，用调整相干长度r0控制相位板的随机特性，图像噪声信噪比为40 dB，采用盲反卷积算法解码码图像，每次用10 幅图像，100 次算法迭代。

图2为像散像差模拟实验结果，最大像散2λ，中心波长500 nm，包括原始图像、像散图像、编码短曝光像和复原图像，以及对应的对数振幅谱图像(lg(1+ |·|2)).图2(b)为未编码的像散图像，从振幅谱图像可见明显的像散特征，图2(c)为经编码后的像散图像，可以看出像散已被削弱，图2(d)为图2(c)的复原解码图像，像差已被消除。

图3为混合像差编码模拟实验，同时有3λ 离焦和2λ 像散图像的实验结果。图3(b)是同时有离焦和像散的像差图像，图3(c)是图3(b)的编码图像，图中可见像差经编码后明显被削弱，图3(d)是编码图像的复原，结果像差已被消除。

从模拟实验结果可以看出，所提出的方法不仅能消除单一的像差，而且能消除混合像差，包括非对称像差的情况。实验中有意在土星附近添加3 颗衍射成像不可分辨的小星，通过实验展示所提出方法的分辨力特性。从图中的结果可以看出，随机波前扰动使光学像差的影响力下降，这在振幅谱图像中更加明显。从复原解码图像的振幅谱显示，恢复图像的频率成分超过了光学衍射截止频率，已达到或接近超衍射极限分辨率的水平。

图4为复原解码图像的估计误差与算法迭代次数的关系，显示了算法的收敛特性，估计误差的定义为

图2 像散图像模拟实验Fig.2 Astigmatic image simulation experiment

由图4中可见，图像估计误差随迭代次数增加而下降，在迭代达到一定次数时，估计误差变化已很小，说明这时增加迭代次数对改进恢复图像的质量已无多大意义;无噪声与有噪声的复原解码情况相比，无噪声情况下估计误差较小，算法收敛更快。

计算机模拟结果表示，通过随机波前编码和数字图像处理方法可以消除光学像差对图像的影响，相位板产生的随机波前改变了光学系统入瞳面上的波前性质，光学像差从原来固定性质变为随机特性，当随机波前的随机性达到一定的水平，光学像差对图像的影响就会被削弱。虽然随机波前使光学像差的影响减弱，图像分辨率由此下降，但是真实物的信息仍然隐藏在扰动图像中，当用盲反卷积算法在消除图像中随机波前扰动时，光学像差随着一起被消除。还可以看出，通过数字图像处理随机扰动图像，复原解码图像的分辨率不仅好于像差图像，而且分辨率达到光学系统衍射极限水平。

图3 混合光学像差图像模拟实验Fig.3 Mixed optical aberrations simulation experiment

为了测试混合成像系统的性能，进行了实验室实验。在Coolsnap 数字CCD 相机近入瞳处放置随机相位板，对模拟图像进行成像，拍摄时故意产生一定离焦，如图5(a)所示。图5(b)为盲反卷积算法100 次迭代复原解码图像，实验结果显示复原解码后图像已没有离焦的影响。

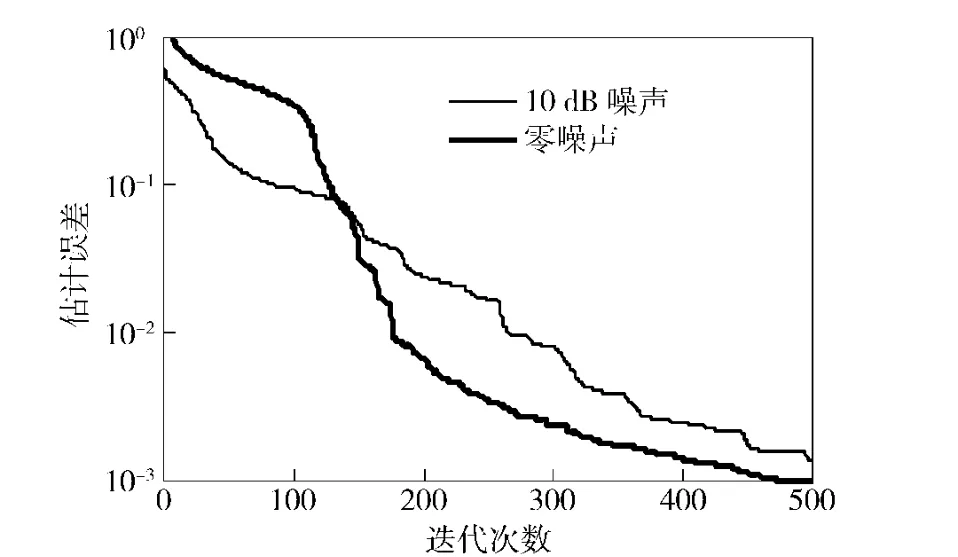
图4 算法迭代次数与复原图像估计误差关系Fig.4 Relationship of algorithm iterations and restored image estimate error

图5 实验室实验图像Fig.5 Experiment image of laboratory

4 结论

本文展示了一种对传统光学像差不敏感的混合光学成像系统，系统包括2 部分:传统光学系统和数字图像处理。在光学系统的孔径光阑上加装一个随机相位板，对有像差的图像进行编码，用数字图像处理方法复原编码图像获得高分辨图像。编码图像复原算法采用盲反卷积，并采用频域共轭梯度优化方法，提高复原速度，通过盲反卷积复原编码图像，使图像中随机扰动和噪声得到有效消除。计算机模拟和实验室结果显示，所提出的混合光学成像系统在一定像差范围内具有不受光学像差影响，并具有抑制噪声的能力，成像质量达到或接近光学系统衍射极限水平。通过采用随机编码相位板混合光学成像系统，可以降低光学设计和加工成本，在消除传统光学系统像差和提高光学系统成像质量的方法上提供了一个新的途径。

References)

［1］ Born M，Wolf E.Principles of optics［M］.7th ed.London:Cambridge University Press，1999.

［2］ Geiser Martial.Strehl ratio and aberration balancing［J］.J Opt Soc Am，1991，8:164-170.

［3］ Berge T.Aberration balancing in rotationally symmetric lenses［J］.J Opt Soc Am，1974，64:1083-1091.

［4］ Castaneda J O，Berriel-Valdos L R.Zone plate for arbitrary high focal depth［J］.Appl Opt，1990，29:994-997.

［5］ Ben-Eliezer E，Zalevsky Z，Marom E，et al.Radial mask for imaging system that exhibit high resolution and extended depth of field［J］.Appl Opt，2006，45:2001-2013.

［6］ Pauca V P，Plemmons R J，Prasad S T，et al.Intergrated opticaldigital approaches for enhancing image restoration and focus invariance［J］.Proc of SPIE，2003，5205:348-357.

［7］ Zalevsky Z，Shemer A，Zlotnik A，et al.All-optical axial super resolving imaging using low-frequency binary-phase mask［J］.Opt Express，2006，14:2631-2643.

［8］ Hui Z，Huajun F，Qi L.Research on design of optimum phase mask for wave-front coded imaging system［J］.Proc of SPIE，2007，6834:68342.

［9］ George N，Chi W.Computational imaging with the logarithmic asphere:theory［J］.J Opt Soc Am，2003，A20:2260-2273.

［10］ Dowski E R，Cathey W T，Bradburn S C.Aberration invariant optical/digital incoherent systems［J］.Optical Review，1996，3(6A):429-432.

［11］ Cathey W T，Dowski E R.New paradigm for imaging system［J］.Appl Opt，2002，41(29):6080-6092.

［12］ Amikam Borkowski，Zeev Zalevsky，Emanuel Marom，et al.Enhanced geometrical superresolved imaging with moving binary random mask［J］J Opt Soc Am，2011，A28:566-575.

［13］ 马拉卡拉D.光学车间检验［M］.白国强，薛君敖，译.北京:机械工业出版社，1983，461.Malacara D.Optical shop testing［M］.BAI Guo-qiang，XUE Jun-ao，translated.Beijing:China Machine Press，1983，461.(in Chinese)

［14］ Tatarski V I.Wave propagation in a turbulent medium［M］.New York:McGraw-Hill，1961.

［15］ Ayers G，Dainty J.Iterative blind deconvolution method and its application［J］.Opt Lett，1988，13(7):547-549.

［16］ Schulz T.Muliframe blind deconvolution of astronomical images［J］.J Opt Soc Am，1993，A10(5):1064-1073.

［17］ Press W H，Teukolsky S A，Vetterling W T，et al.Numerical recipes in C++:the art of scientific computing［M］.2nd ed.Cambridge:Cambridge University Press，2002.