线圈型电磁发射器磁场构型的设计与分析

朱英伟，李海涛，严仲明，付磊，2，王豫，2

(1.西南交通大学 电气工程学院，四川 成都610031;2.西南交通大学 磁浮技术与磁浮列车教育部重点实验室，四川 成都610031)

线圈型电磁发射器的基础工作之一是设计符合推射要求的磁场构型，从而满足发射所需要的电磁加速力。这里的磁场构型指的是特定的线圈形状或组合产生所需要的空间磁场强度或磁场梯度。实际应用的线圈，除了要求磁场源有一定的磁场强度外，还希望磁场在工作空间有一定的分布形态; 如磁场强度均匀、磁场强度沿某一方向的梯度均匀等。如核磁共振测场仪的定标，要求磁场源在探头所占空间内具有与仪器相当的磁场均匀度。再如用法拉第法测量样品的磁矩，要求辅助磁场源在样品所占空间的磁场强度沿着与磁场垂直的方向的梯度非常均匀［1］。

传统的线圈型发射器的驱动线圈均为直螺线管线圈结构，其磁场构型较为简单，对抛体电枢产生的电磁作用力主要表现为径向压缩力，而轴向加速力较小［2］，这也是造成系统发射效率低的原因之一。为了提高抛体所受到的轴向加速力，推射磁场构型的设计准则是: 1)提高驱动线圈产生的磁场强度及其梯度大小，2)增大梯度磁场对抛体作用的空间和时间范围［3-6］。

1 线圈型电磁发射加速力的表达式

线圈型电磁发射的原理模型，如图1所示，螺线管线圈产生推射磁场，将抛体电枢等效为电流圆环，磁场对电流有电磁作用力。

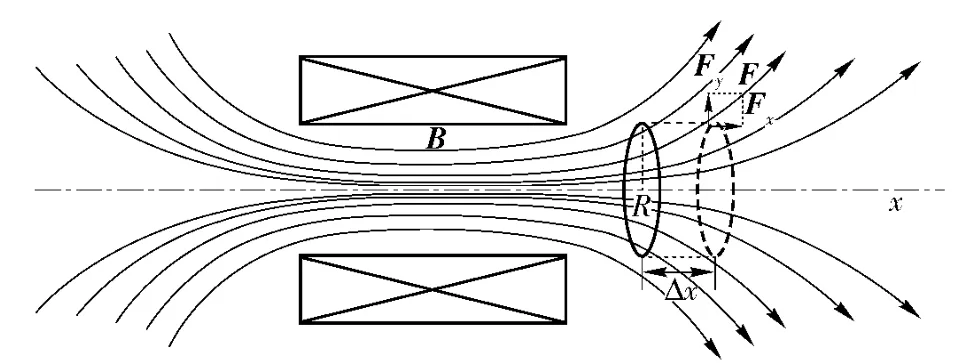
图1 电流圆环在螺线管线圈中的受力示意图Fig.1 Sketch of current ring in solenoid coil

在导线环上选电流元Idl，此电流元受的磁力为dF=Idl × B.将dF 分解为轴向与径向2 个分量dFx和dFy.由于磁场和电流的分布对x 方向的轴对称性，所以环上各电流元所受的磁力的径向分量dFy的矢量和为0.而由于各电流元所受的轴向磁力dFx方向相同，因此，电流圆环所受的总磁力的大小为

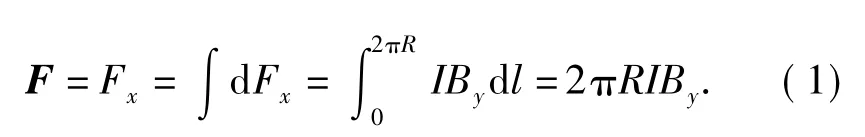
当电流圆环沿轴向移动位移Δx 时，取图1虚线所示的圆柱高斯面，根据磁通连续性定量∮SB·dS =0可得

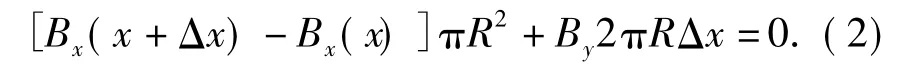
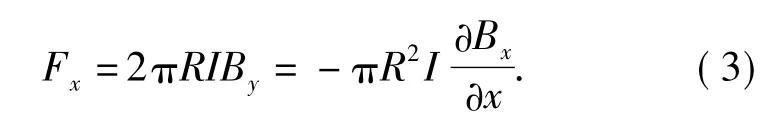
线圈型电磁发射的原理基于电流圆环在螺线管线圈磁场中的受力。分析受力情况可以知道，当电流圆环与螺线管线圈电流异向时，电流圆环受到磁场径向压缩力和轴向排斥力作用，轴向排斥力作为线圈型电磁发射的加速力。在螺线管内部附近磁场Bx≫By，因此，电流圆环受到的径向压缩力远大于轴向加速力。该加速力表达式表明，加速力的大小与驱动线圈产生磁场的梯度有关。螺线管线圈产生的轴向磁场的梯度仅在两端口处较大，因此，加速力作用主要表现在线圈端口附近处，而其它地方加速力较弱。由此可见，长螺线管线圈的电磁加速力利用率不高，根本原因是磁场构型不利于加速力的产生和作用。线圈型电磁发射要求驱动线圈在抛体电枢运动方向上产生梯度较高的磁场，才能获得较大的加速力，本质上就是设计满足发射需求的磁场构型。

2 螺线管线圈磁场构型的设计考虑

线圈的种类和形状决定了磁场的形态。一般线圈型电磁发射器或同轴驱动器的线圈为密绕的直螺线管，其磁场分布为:在螺线管中心附近轴线上各点磁场基本上是均匀的，到管口附近磁感应强度值逐渐减小，出口以后磁场很快地减弱。磁力线在螺线管中心处平行于螺线管轴线，向两端延伸时逐渐发散。单螺线管的最大场强点在内表面的中部，最小场强点在绕组内垂直于轴线的对称面上靠近外表面的地方，如图2(a)所示。螺线管线圈的磁场分布形态如图2(b)所示。

通常，用线圈内半径作为长度单位来对线圈的其它尺寸以及点的坐标进行归一化，即令α =a2/a1，β=b/a1.a1，a2分别为螺线管线圈的内半径和外半径，b 为螺线管的半长或半高。这样，用α 和β 两个参量来描述了螺线管线圈的几何形状。

对于截面均匀电流密度为J 的螺线管线圈，其中心点磁场Hz(0，0，0)可以表达为

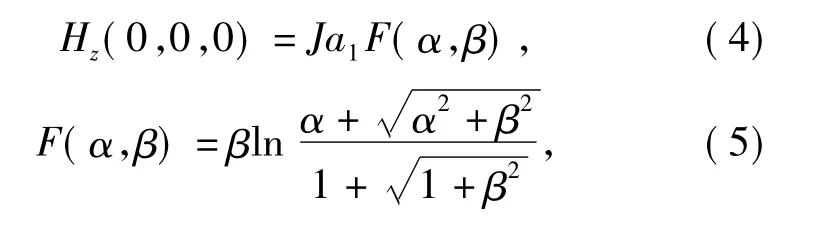
式中: F(α，β)为螺线管形状函数，与线圈几何形状有关，由线圈的内、外半径和线圈长度决定。由中心点磁场的表达式知，在线圈结构形状一定的情况下，磁场强度与线圈载流密度成正比。因此，改变线圈的结构形状能够获得较大的磁场强度，或者获得一定的磁体梯度形态。

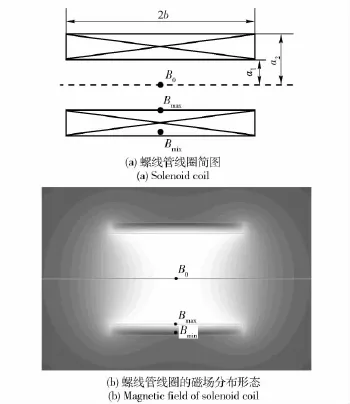
图2 螺线管线圈的磁场构型Fig.2 Magnetic field configuration of solenoid coil

一般螺线管线圈是密绕细导线，导线的截面积与线圈的其余尺寸相比很小，所以可以认为导线中的电流密度是均匀的。当线圈导线材料电阻率为ρ，绕组内的电流密度为J，导线的占空系数为λ，线圈绕组的体积为V 时，线圈消耗的功率为

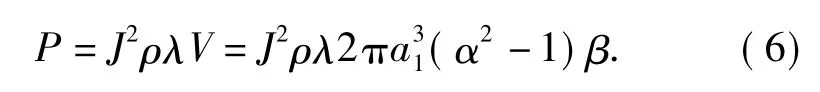
将线圈功耗中的电流代入中心点磁场强度，可得关系式

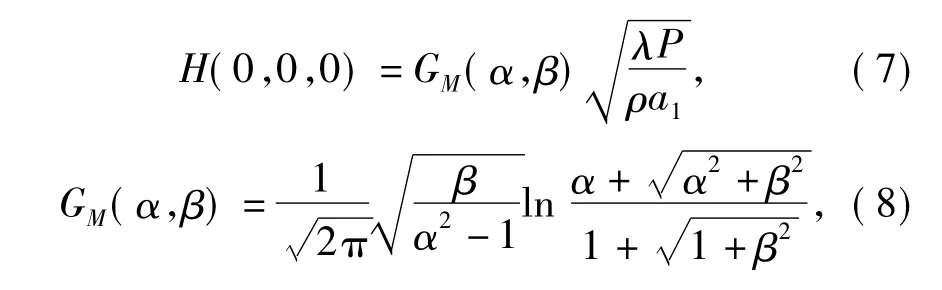
式中:GM(α，β)为均匀电流密度线圈的效率系数，它与线圈的几何形状有关，而与尺寸大小无关。在相同的功耗下，GM因子越大的线圈产生的磁场强度也越大。计算表明，对于截面电流密度均匀的线圈，在相同的功耗下，α =3 和β =2 这种几何形状的线圈产生的磁场强度最大。因此，在额定的电源功率下，为了获得最大的磁场，应尽可能选用这种形状。

3 螺线管线圈磁场构型的仿真分析

3.1 不同厚长比矩形截面螺线管线圈的磁场构型

使用电磁场有限元分析软件Ansoft Maxwell 对线圈型电磁发射模型进行静磁场仿真分析［7-10］，其中包括磁场的构型计算、驱动线圈与抛体线圈之间的互感及电磁力计算。对单级线圈型电磁发射进行二维轴对称建模，其仿真模型如图3所示。驱动线圈和抛体线圈均为密绕螺线管，矩形截面电流密度均匀，设电流密度为109A/m2.驱动线圈内半径a1=32 mm，轴线长b=40 mm，外半径a2=kcb +a2，其中，kc为驱动线圈的径向厚度与轴向长度的比值。抛体线圈内半径为23 mm，外半径为30 mm，轴线长度为40 mm.考虑不同厚长比矩形截面螺线管线圈的磁场构型，采用静磁场参数化仿真，设kc=0.4、0.6、1.0 和1.6.同时，设抛体线圈的位置为参数变量，计算抛体在轴线不同位置时驱动线圈与抛体线圈之间的互感和作用力。驱动线圈产生的磁场由磁矢势方程导出，驱动线圈与抛体之间的互感根据磁链与电流的矩阵关系计算，驱动线圈对抛体线圈的电磁力由虚功原理来计算。仿真模型网格采用静磁场自适应划分，求解计算的能量误差设置为0.01%.

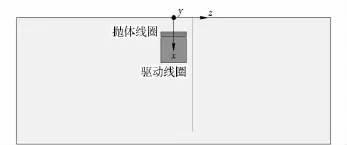
图3 仿真模型Fig.3 Simulation model

图4为驱动线圈与抛体线圈之间的互感随抛体位置的变化趋势，图5为驱动线圈对抛体线圈的作用力随位置变化的情况。随着kc增大，线圈增厚，线圈匝数增多，驱动线圈与抛体线圈之间的互感值增大，2 者之间的作用力增强。线圈变厚，最大作用力值出现在线圈轴线上的位置发生变化，最大力值出现点离线圈中心变远，较大力值的作用范围增大。因此，驱动线圈的设计要保证一定的厚度，才能够保证驱动线圈与抛体线圈之间互感储能，从而达到抛体线圈加速所需要的作用力值。

3.2 不同截面形状螺线管线圈的磁场构型

考虑不同截面形状螺线管线圈产生的磁场构型，线圈横截剖面分别为矩形、正方形、梯形、和三角形。约束条件是各线圈的内半径相同为10 mm，要求截面积相等为800 mm2，同时截面通载电流密度相等为109A/m2.仿真计算各种截面线圈的空间磁场分布如图6所示。结果表明，正方形截面线圈产生的磁感应强度值最大，磁场梯度也最大;梯形截面线圈产生的磁场最小。

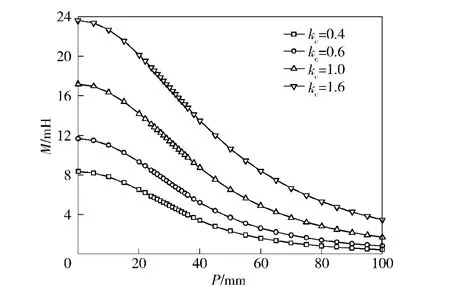
图4 驱动线圈与抛体线圈之间的互感随位置变化趋势Fig.4 Mutual inductance between driving coil and projectile

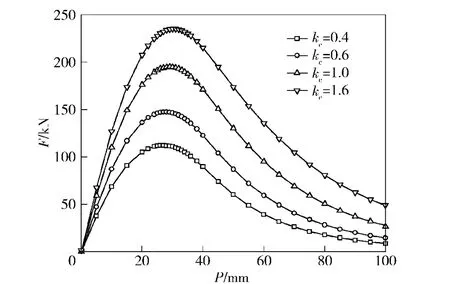
图5 驱动线圈与抛体线圈之间的作用力随位置变化趋势Fig.5 Magnetic force between driving coil and projectile

图6 不同截面线圈的空间磁感应强度分布Fig.6 Magnetic field configuration of different coils

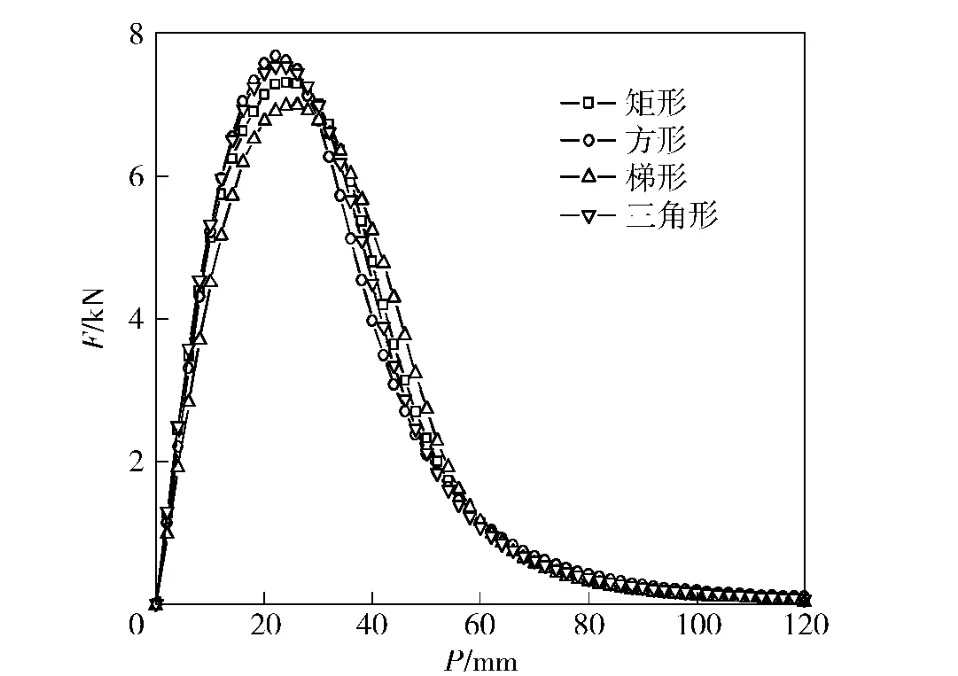
图7 不同截面线圈与抛体之间作用力随位置变化曲线Fig.7 Magnetic force vs.position of different coils

考虑不同截面驱动线圈对抛体的作用力效果，采用静态磁场仿真模块参数化计算。抛体线圈截面为矩形，其内半径为4 mm，外半径为8 mm，轴线长度为40 mm，截面电流密度为109A/m2.不同截面驱动线圈对抛体线圈的作用力变化曲线，如图7所示。由结果可知，正方形截面线圈对抛体的作用力最大，梯形截面线圈对抛体作用力最小。可见，在静态磁场中，为了获得最大的电磁力，可以考虑选取正方形截面的螺线管线圈。但是，在瞬态电磁发射过程中，考虑综合发射效果，正方形截面线圈的发射速度并不一定最大，发射效果主要由初始电源和能量转换效率决定。事实上，电源一定，驱动线圈和抛体线圈的耦合系数一定，各种截面线圈的发射效果基本一致。

作为相对性问题考虑，对于不同截面的抛体线圈进行类似计算，选取矩形截面抛体线圈和正方形截面抛体线圈进行静态磁场参数化计算，约束条件是抛体截面积相等、载流密度相等，抛体线圈与驱动线圈之间气隙厚度相同，计算结果如图8所示。由于矩形截面抛体线圈与驱动线圈之间的耦合互感较大，结果表明矩形截面抛体线圈受力较大。

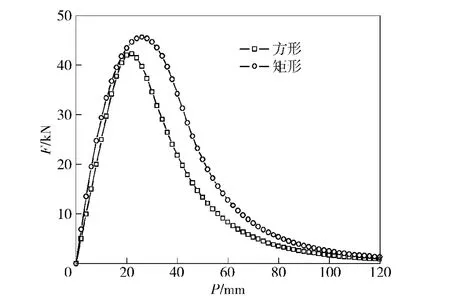
图8 方形截面抛体和矩形截面抛体的电磁力比较曲线Fig.8 Magnetic force vs.position of different coils

4 结论

线圈型电磁发射器的加速力与驱动线圈的磁场构型有关，线圈产生的磁场梯度越大，抛体与驱动线圈之间的互感梯度越大，抛体线圈受到的加速力就越大。常规直螺线管线圈产生的轴向磁场的梯度仅在两端口处较大，造成电磁加速力利用率不高。对于线圈型电磁发射器的设计要综合考虑磁场构型、功率损耗和储能要求。在静态磁场中，相同截面安匝电流的情况下，驱动线圈采用正方形截面螺线管，能够对抛体产生较大的电磁作用力，抛体线圈采用矩形截面线圈能够受到较大的电磁力。建议采用非常规截面线圈或多线圈组合的方式，如比特线圈或高姆线圈，从而增强抛体线圈所受到的加速力，也可以降低驱动线圈电流的幅值，减弱对电源系统的功率要求，从而减小损耗，提高系统的发射效率。

References)

［1］张宝裕，刘恒基.磁场的产生［M］.北京: 机械工业出版社，1987.ZHANG Bao-yu，LIU Heng-ji.Magnetic field generation［M］.Beijing:Mechanical Industrial Press，1987.(in Chinese)

［2］王莹，肖峰.电炮原理［M］.北京:国防工业出版社，1995.WANG Ying，XIAO Feng.Physics of electric launch［M］.Beijing:National Defense Industry Publishers，1995.(in Chinese)

［3］Putman P，Salama K.Optimization of energy conversion in monolithic superconducting magnets［J］.IEEE Trans on Applied Superconductivity，2003，13(2): 2146 -2149.

［4］Kaye R.Operational requirements and issues for coilgun electromagnetic launchers［J］.IEEE Trans on Mag，2005，41(1):194-199.

［5］Balikci A，Zabar Z，Birenbaum L，et al.On the design of coilguns for super-velocity launchers［J］.IEEE Trans on Mag，2007，43(1):107 -110.

［6］Babic S，Akyel C.Magnetic force calculation between thin coaxial circular coils in air［J］.IEEE Trans on Mag，2008，44(4):445-452.

［7］刘国强，赵凌志，蒋继娅.Ansoft 工程电磁场有限元分析［M］.北京:电子工业出版社，2005.LIU Guo-qiang，ZHAO Ling-zhi，JIANG Ji-ya.Ansoft engineering electromagnetic field finite element analysis［M］.Beijing:Publishing House of Electronics Industry，2005.(in Chinese)

［8］李建辉，刘秀成，王春明，等.电感储能型线圈炮系统的建模和参数优化［J］.电工电能新技术，2007，26(2):54 -58.LI Jian-hui，LIU Xiu-cheng，WANG Chun-ming，et al.Modeling and parameter optimization of coilgun system with inductive energy storage supply［J］.Advanced Technology of Electrical Engineering and Energy，2007，26 (2):54 -58.(in Chinese)

［9］周媛，严萍，袁伟群，等.电磁轨道发射装置中导轨几何参数对电感梯度的影响［J］.电工电能新技术，2009，28(3):23 -27.ZHOU Yuan，YAN Ping，YUAN Wei-qun，et al.Effect of rail geometrical parameters on inductance gradient of EML［J］.Advanced Technology of Electrical Engineering and Energy，2009，28(3):23 -27.(in Chinese)

［10］林庆华，栗保明.电磁轨道炮三维瞬态涡流场的有限元建模与仿真［J］.兵工学报，2009，30(9):1159 -1163.LIN Qing-hua，LI Bao-ming.Finite element analysis of 3D transient eddy field in electromagnetic railgun［J］.Acta Armamentarii，2009，30(9):1159 -1163.(in Chinese)