大气湍流和色散导致脉冲展宽的分析比较
2011-02-21陆红强赵卫谢小平
陆红强,赵卫,谢小平
(1.中国科学院西安光学精密机械研究所 瞬态光学与光子技术国家重点实验室,陕西西安710119;2.中国科学院 研究生院,北京100039)
航天技术的发展使得卫星载荷数量增加,获取的信息在空间分辨率、时间分辨率以及实时性上要求越来越高,这使得星地/星间通信链路带宽需求急剧增加。光载波的高频使激光通信比微波通信传输带宽高2~3 个数量级,由于传输带宽高、保密性好以及发射运行成本低等特点使星地/星间激光通信越来越引起人们重视[1]。在地面自由空间激光通信实验中,单通道最大传输速率为160 Gbit/s[2]; 在星地激光通信演示验证实验中,单通道最大传输速率为5.6 Gbit/s[3];在地面光纤传输系统中,采用光时分复用技术可以实现单通道1.28 Tbit/s 的最大传输速率[4]。由于目前星地激光通信传输速率低于10 Gbit/s,光信号脉冲脉宽大于50 ps; 而对于地面160 Gbit/s 自由空间激光通信实验系统而言,其传输距离很短(0.2 km),所以在实际空间激光通信系统对于大气湍流和大气色散导致脉冲展宽忽略不计。
随着空间激光通信系统传输速率的增加,由大气湍流和大气色散导致的脉冲展宽将使得相邻脉冲信号间产生码间干扰,影响通信系统的传输性能和带宽。为此,文献[5 -6]提出在传输介质中脉冲展宽的2 种可能机制;文献[7 -8]根据二频互相关函数和四频交叉相关推导出脉冲展宽的解析表达式;文献[9]分析计算由于脉冲展宽而导致的码间干扰,但是其计算的码间干扰与调制信号占空比无关,这不符合事实;文献[10]研究了非视距多路径散射导致的脉冲展宽;文献[11]对云层粒子对激光的多次散射引起脉冲信号展宽以及信号的码间干扰进行了研究;文献[12]对大气湍流、色散和光学系统导致的脉冲展宽进行分析计算,但是把大气压力和温度处理为常数,这偏离实际情况。考虑到星地长距离激光通信系统中传输带宽的不断增加,同时据了解还没有相关文献根据实测的大气参数(温度和压强)对大气色散导致的脉冲展宽进行数值计算。本文首先计算得到大气湍流、传输距离、输入脉宽等参数与脉冲展宽量之间的关系曲线,其次根据文献[13]给出新疆戈壁地区大气压强和温度随着高度的分布数据,计算出大气色散导致的脉冲展宽以及对系统传输带宽的影响。
1 大气湍流导致脉冲展宽
假设调制输出的光信号为高斯脉冲,其载波频率为ω0,振幅为v(t),则调制脉冲信号为
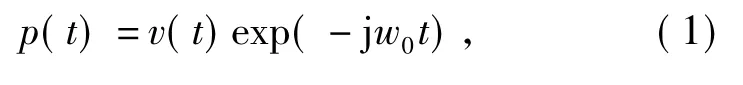
其振幅表达式为
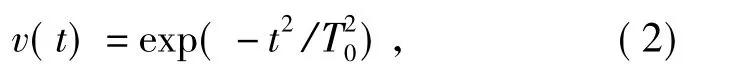
式中: T0为调制脉冲振幅1/e 点处的半宽。经过距离为L 的湍流路径传输后,接收端脉冲强度分布为[7-8]
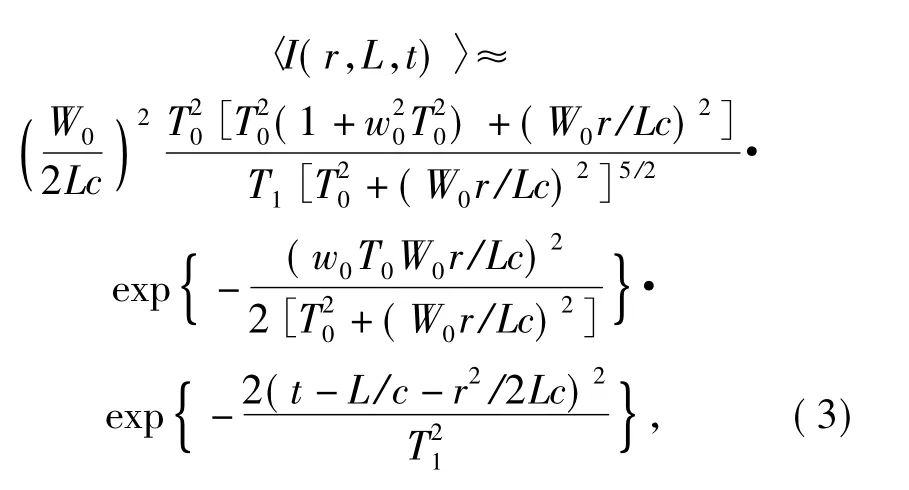
式中:T1为接收端脉冲振幅1/e 点处的半宽; W0为发射端光斑半径。在计算中采用Hufnagel-Valley 湍流模型,其湍流大气折射率结构常数为
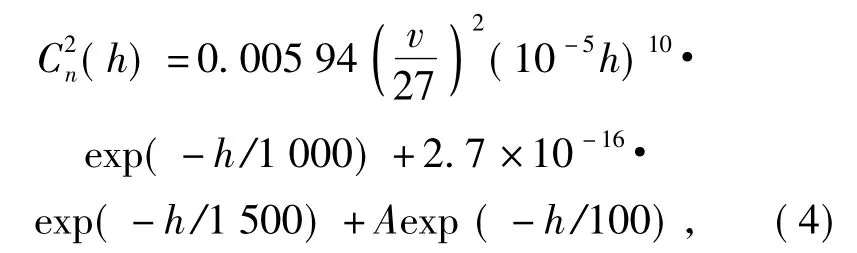
式中: v 为随机风速(m/s); h 为海拔高度(m); A为与地表面湍流大气折射率结构常数C2n有关的常数,用于表征大气湍流的强弱。大气湍流外尺度和内尺度为
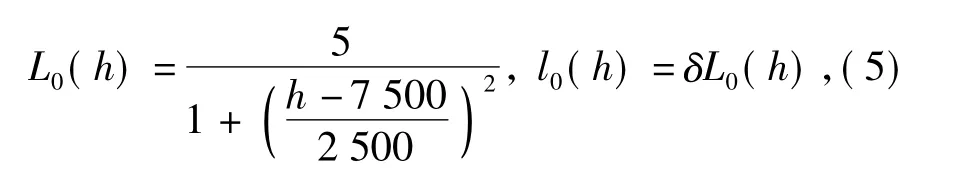
其中0<δ<1.经过距离为L 的湍流路径传输后,接收端脉冲半宽[7-8]
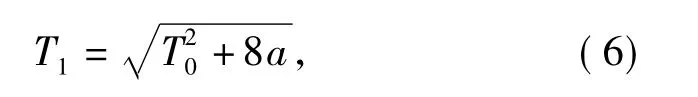
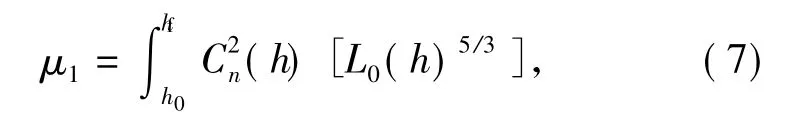
式中:h0为光发射端机的高度; hf为光接收端机的高度。
在图1计算中取激光信号波长为1.55 μm,传输距离为100 km,ξ 为0.005[8].文中所有关系曲线的计算条件均附于相应的图中,因此对于每次计算条件不进行重复描述。根据(4)式~(7)式得到脉冲展宽量和传输天顶角ξ、输入脉宽T0的关系曲线如图1所示。
图1(a)、(b)分别对应与A 为1.7 ×10-14m-2/3(弱大气湍流)和1.7 ×10-13m-2/3(强大气湍流)时[8],接收端脉冲展宽量与输入脉宽、传输天顶角之间的关系曲线。随着输入脉宽的增加,脉冲展宽量迅速降低。在图中计算条件下,当输入脉宽大于40 fs 时,脉冲展宽量可以忽略不计。激光信号以不同天顶角传输时,由于经过大气的传输距离不同,所以脉冲展宽量也不同。在实际星地激光通信中,要尽可能地选择小天顶角进行通信。脉冲展宽量与传输天顶角、输入脉宽的部分计算数值,如表1所示。
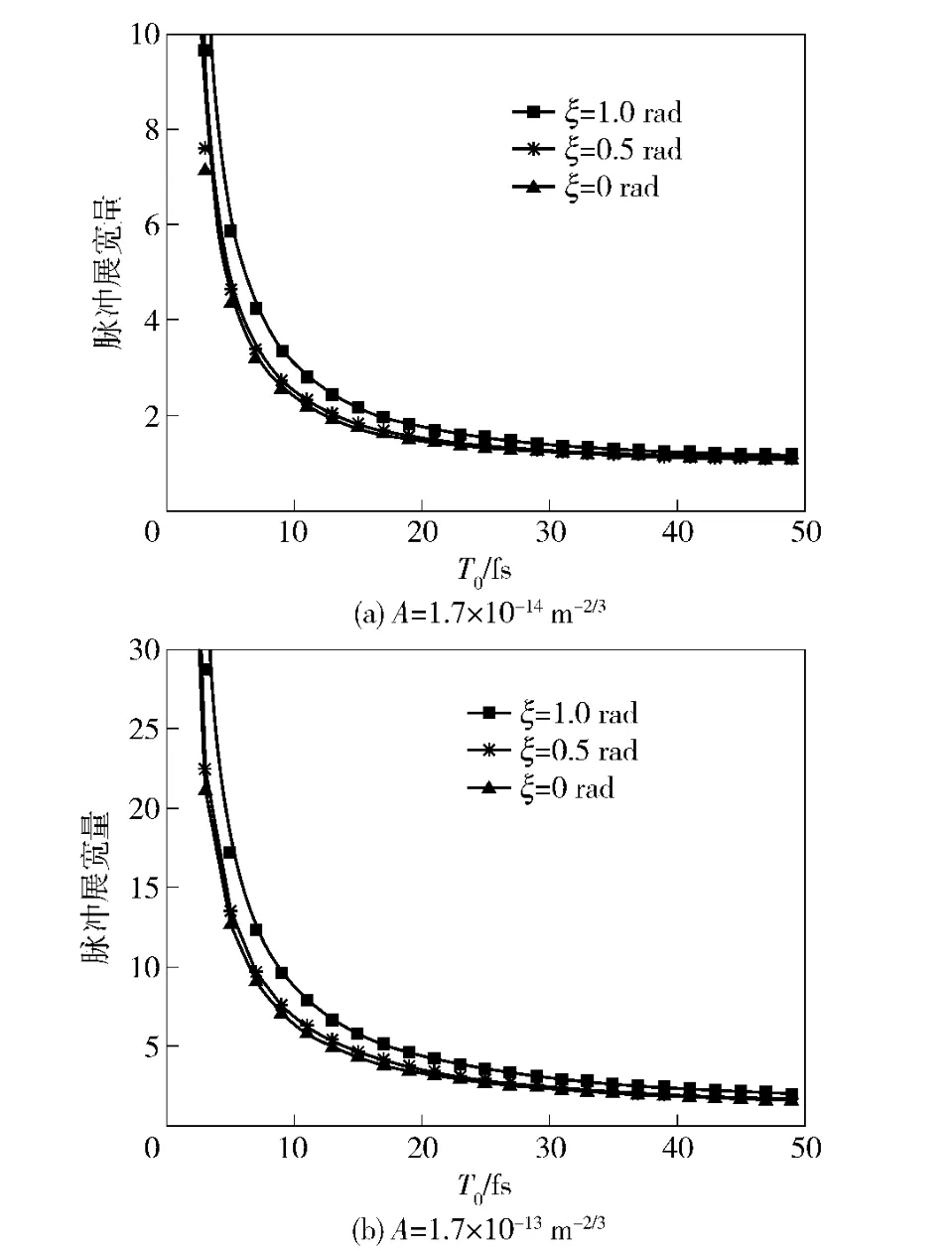
图1 脉冲展宽量与传输天顶角、输入脉宽的关系曲线Fig.1 Relation of pulse broadening ratio to zenith angle and input pulse width

表1 脉冲展宽量与传输天顶角、输入脉宽关系Tab.1 Datum of pulse broadening ratio
图2(a)、(b)分别对应于输入脉宽为20 fs 和1 ps时,不同传输距离下展宽的脉冲波形。由于脉冲展宽,信号振幅将会下降,文中对接收的脉冲振幅进行了归一化处理。随着传输距离的增加,脉冲展宽量的逐渐变大,图2中标注了不同传输距离下脉冲的展宽量。如图2(b),输入脉宽为1 ps、强湍流(A 为1.7 ×10-13m-2/3)条件下,当传输距离小于5 000 km时,脉冲展宽可以忽略不计(图中多个脉冲波形重合)。即使经过38 500 km 长距离传输,脉冲的展宽量(1.52)也很小。考虑到不同的湍流强度和传输距离,可以认为当脉宽大于0.5 ps 时,大气湍流导致的脉冲展宽可以忽略不计。接收端脉冲展宽量与输入脉宽、传输距离的部分计算数值如表2所示。
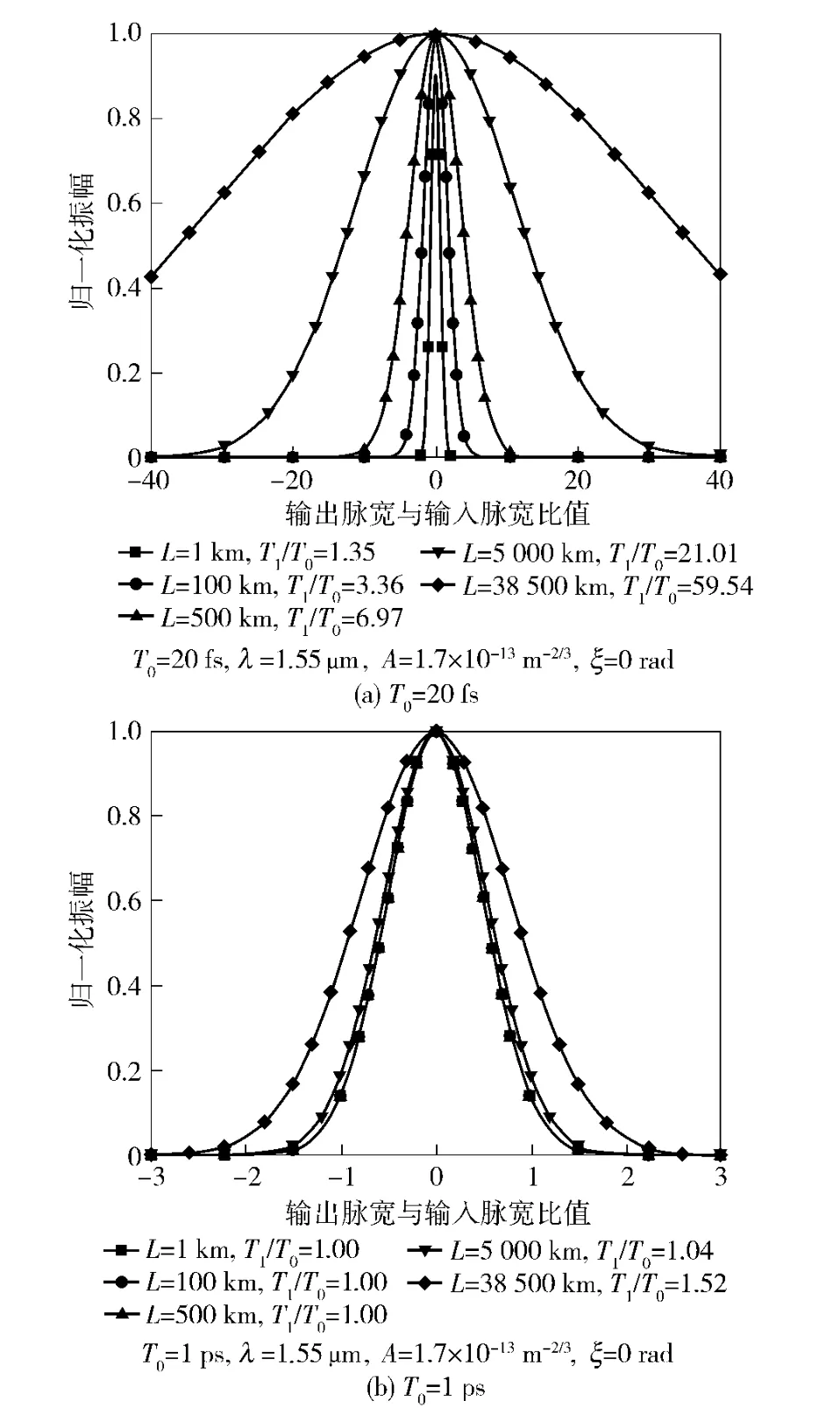
图2 不同传输距离下展宽的脉冲波形Fig.2 Broadened pulse waveform in different propagating

表2 脉冲展宽量与输入脉宽、传输距离关系Tab.2 Relation pulse broadening ratio to input pulse width and propagating distance
2 大气色散导致脉冲展宽
地球大气聚集在地球表面,并且从地面向上延伸至数百公里。从地面到20 km 所包含的大气质量占全部大气质量的90%左右; 从地面到50 km 所包含的大气质量占全部大气质量的99.9%[14-15].脉冲传输过程中光谱受到不同程度的衰减和色散,这将导致脉冲展宽或者压缩[16]。对于激光信号在大气中传输而言,大气折射率是一个重要的参数。大气折射率分布与大气压强和温度的分布有关,对于可见光和红外波段大气折射率为[15]
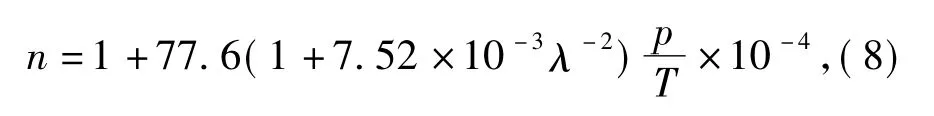
式中:p 为大气压力(Pa); λ为激光波长(μm); T 为温度(K).对于近地面水平链路,可以认为大气压强和温度是定值,大气折射率仅和激光波长有关。对于垂直和斜传链路,由于温度和压强随着海拔高度而变化,因此大气折射率和激光波长、海拔有关。文献[13]给出新疆戈壁地区大气温度和压强随着海拔的分布拟合多项式:

式中:h 为海拔高度(m),将(9)式和(10)式代入(8)式可以得到1.55 μm 波段大气折射率随着海拔的分布曲线,如图3所示。在地表附近大气折射率为1.002 4,随着海拔的增加,大气折射率逐渐减小;当海拔增加到30 km 处,大气折射率已经接近为1,整个大气层内折射率的变化量很小。因此大气对脉冲的色散作用主要发生在地球表面到向上延伸30 km 范围内,在下面的计算中取传输高度值为30 km.不同的测试地点、气候条件下大气折射率并不相同,但是这并不影响大气色散导致脉冲展宽的估算。
激光信号在大气中传播常数β 定义为
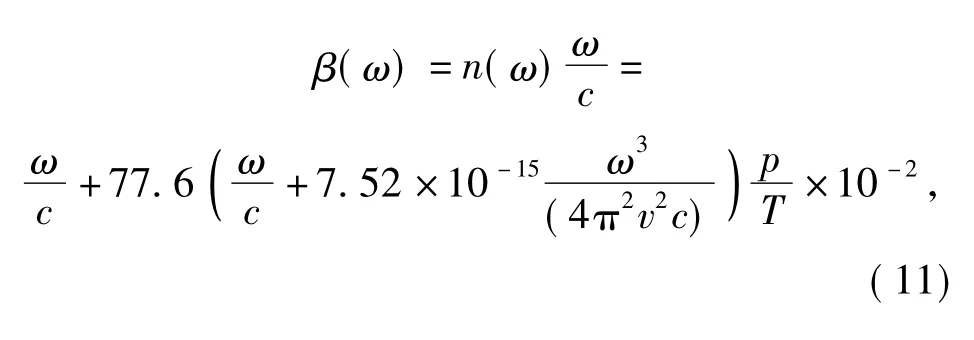
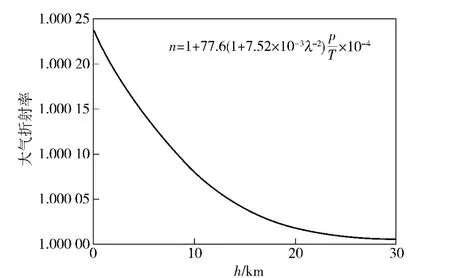
图3 大气折射率随着海拔分布曲线Fig.3 Atmospheric refractive index (n)in different heights
在激光载波ω0处对传播常数β 进行泰勒级数展开,并取前4 项
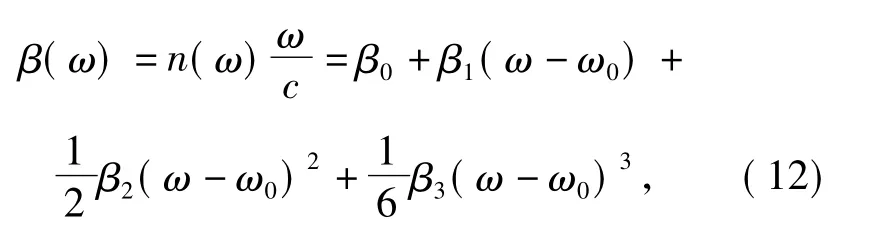
式中:β1、β2和β3为传播常数β 的一阶、二阶和三阶微分,表达分别为
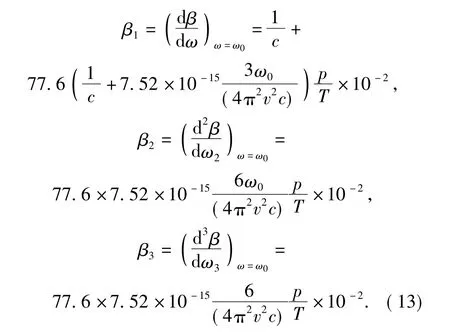
通过对比(13)式可知: β1、β2和β3之间相差一个比例常系数,因此β1、β2和β3随着海拔的分布曲线完全一致。β2随着海拔h 的分布曲线,如图4所示。
在色散和啁啾的共同作用下,经过长度为z 的色散介质传播后,接收端脉冲展开量为[16]
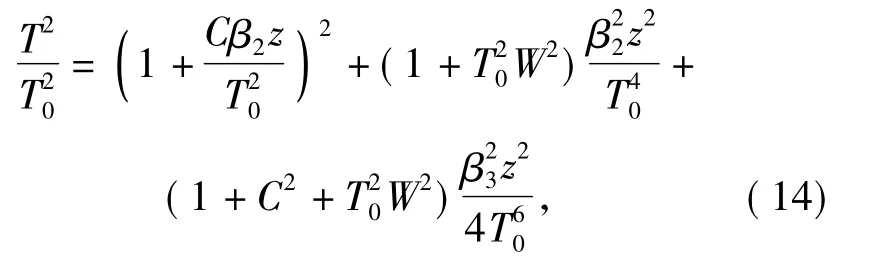
式中:C 为调制输出脉冲的啁啾参数; W 为脉冲信号的均方根谱宽。为了比较β2和β3对脉冲展宽的作用,将(14)式中右边第2 项和第3 项分别标记为A 和B,则
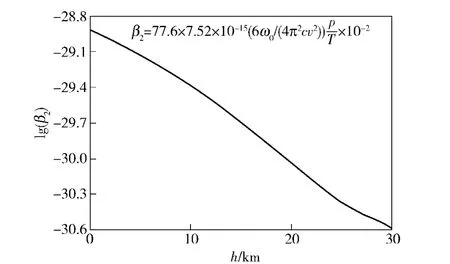
图4 lg(β2)随着海拔的分布曲线Fig.4 Relation of lg(β2)to height
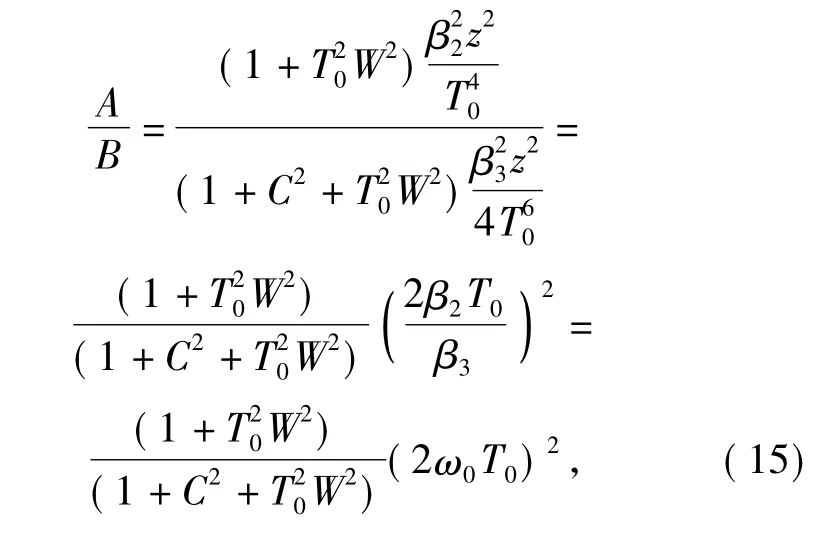
取λ 为1.55 μm; T0为50 ps; C 为2; W 为125 GHz[17],得到A/B≫1,因此在计算大气色散导致脉冲展宽时,β3的作用可以忽略不计。简化后的脉冲展宽为
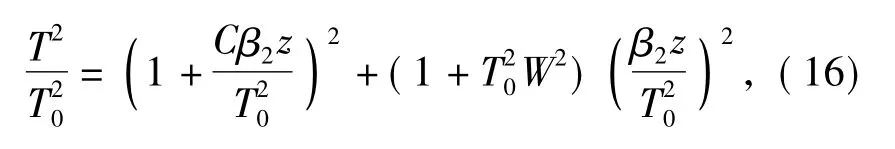
由于大气折射率n 随着高度变化,使得β2与高度有关。在计算大气色散导致脉冲展宽的过程中必须把整个传输通道分为N 段,每段传输高度为Δh.考虑到链路天顶角ξ,每段传输距离为Δh/cos(ξ).当N取值足够大时,可以认为n 和β2在Δh 内是常数。经过每一段大气传输后,脉冲展宽量为
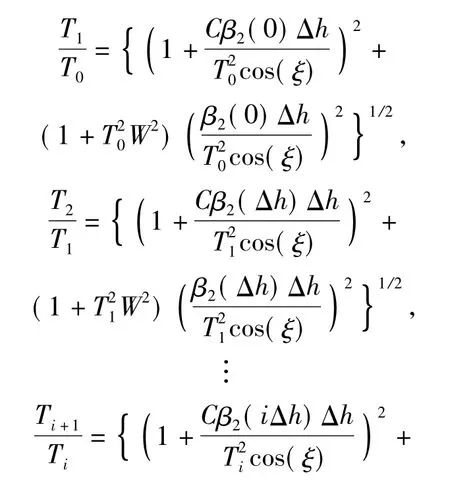
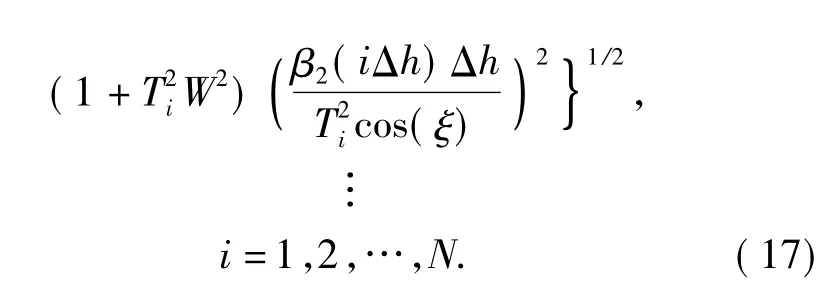
在不同链路天顶角下,脉冲展宽量随着输入脉宽的变化曲线,如图5所示。
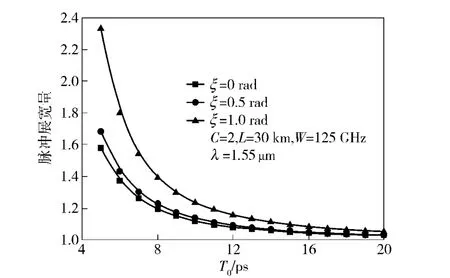
图5 脉冲展宽量随着链路天顶角和输入脉宽的变化曲线Fig.5 Relation of broadening ratio to zenith angle and input pulse width
随着链路天顶角的增大,由于传输距离的增加从而导致脉冲展宽量增大。随着输入脉宽逐渐增大,脉冲展宽量逐渐减小。对于大气色散导致的脉冲展宽:当T0<5 ps 时,脉冲展宽急剧增大;当T0>20 ps 时,脉冲展宽可以忽略不计。当输入脉宽T0>0.5 ps 时,大气湍流导致脉冲展宽可以忽略不计。因此相比于大气色散,大气湍流导致脉冲的展宽量可以忽略不计。
由于大气折射率和激光波长有关,因此对于不同波长的脉冲信号,接收端脉冲展宽量将不同。脉冲展宽量随着激光波长的变化曲线如图6所示。当激光信号波长分别0.850、1.064、1.31 μm 和1.55 μm 时,脉冲展宽量分别为4.027 6、3.056 2、2.469 4和2.146 9.随着激光信号波长的增加,由色散导致的脉冲展宽逐渐降低,这对于空间激光通信中激光波长的选择具有一定的指导意义。
脉冲展宽量随着传输高度的变化曲线,如图7所示。当传输高度分别为1、10、20 km 和30 km 时,脉冲展宽量分别为1.089 6、1.762 6、2.071 2 和2.146 9.随着传输高度的增加,色散导致脉冲展宽效应变弱,脉冲展宽量逐渐趋于恒定值。
经过大气色散作用后,接收端脉冲展宽量随着输入脉宽的增加而减小,接收端脉宽由输入脉宽和脉冲展宽量共同决定。接收端脉宽随着输入脉宽的变化曲线,如图8所示:当初始脉宽为3 ps 时,大气色散导致脉冲展宽量为10.580 5,接收端脉宽为31.741 5 ps;当初始脉宽为15 ps,大气色散导致脉冲展宽量为1.098 5,接收端脉宽为16.477 5 ps.当输入脉宽较小时,大气色散对接收端脉宽起主要作用;当输入脉宽较大时,初始脉宽对接收端脉宽起主要作用。在图8中所示条件下,当输入脉宽为7 ps 左右时,接收端脉宽最小(10.777 9 ps).
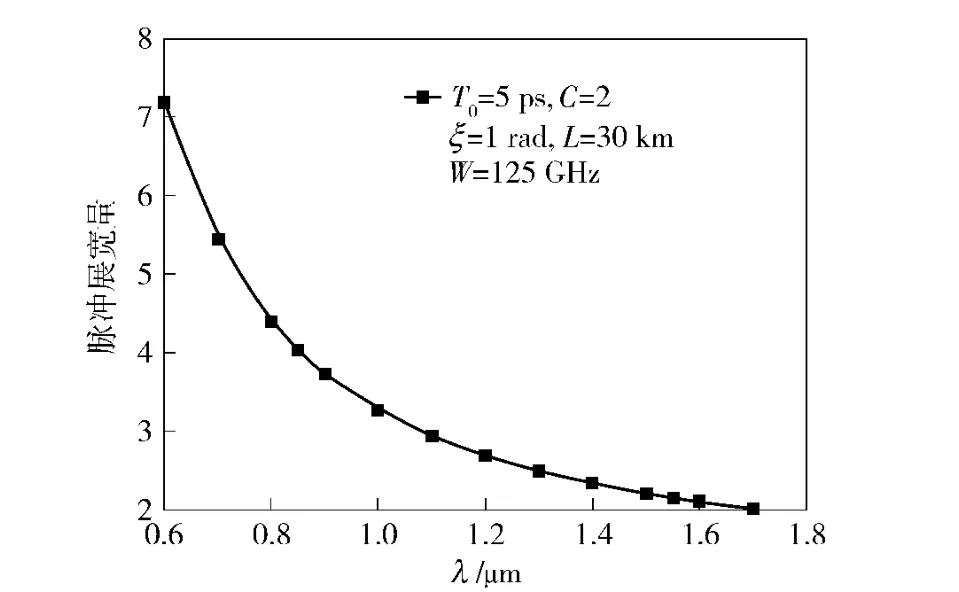
图6 脉冲展宽量随着激光波长的变化曲线Fig.6 Broadening ratios for different wavelengths
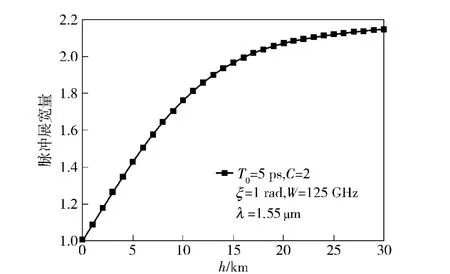
图7 脉冲展宽量随着传输高度的变化曲线Fig.7 Broadening ratio vs.height
为了消除脉冲展宽对系统传输带宽的影响,接收端展宽后脉冲应该保持在比特通道内。对于高斯脉冲而言,展宽后脉宽Tn和系统传输带宽B 应该满足[17]:4BTn<1,此时高斯脉冲能量的95%能够被保持在比特通道内。在不考虑大气色散对脉冲展宽的影响,传输系统带宽随着原始脉宽的增加而减小,其变化关系如图9所示:当初始脉宽为5、7 ps 和10 ps 时,系统的理论传输带宽Btheory分别为50、35.71 Gbit/s 和25 Gbit/s.由于存在大气色散的作用,系统实际传输带宽Bpractice变化关系如图9所示: 当初始脉宽为5、7 ps 和10 ps 时,系统的传输带宽分别为21.46、23.22 Gbit/s 和20.23 Gbit/s.系统实际传输带宽将受限于大气色散,尤其当调制输出脉宽较小时。
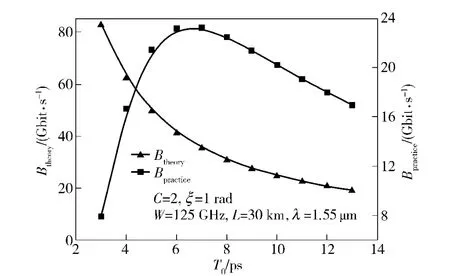
图9 系统传输带宽随着输入脉宽的变化曲线Fig.9 Achievable bandwidth vs.input pulse width
4 结论
分析计算在大气湍流的影响下,接收端光脉冲强度分布和脉宽随着大气湍流强度、传输距离、传输链路天顶角、输入脉宽等因素的关系曲线。根据实测大气温度和压强分布数据,计算大气折射率n 和色散常数β 的二阶微分β2和三阶微分β3.推导出由于大气色散的影响,接收脉宽随着输入脉宽、激光信号波长、传输链路天顶角以及传输距离等因素的变化关系。基于文中图例的数值计算条件,结果表明:1)当输入脉宽大于0.5 ps 时,大气湍流导致脉冲展宽可以忽略不计;当输入脉宽大于20 ps 时,色散对脉宽的影响可以忽略不计; 2)随着激光信号波长的增加,由于大气色散导致的脉冲展宽逐渐降低;3)输入脉宽较小时,大气色散对接收端脉宽起主要作用;当输入脉宽较大时,初始脉宽对接收端脉宽起主要作用。4)大气色散将导致空间激光通信系统的传输带宽下降,在特定条件下通信系统存在一个最小接收脉宽和最大传输带宽。实际系统参数不尽相同,但是文中涉及的分析方法可以有效应用于评估大气湍流和大气色散对系统通信性能的影响。
References)
[1]Toyoshima M.Trends in satellite communications and the role of optical free-space communications[J].Journal of Optical Networking,2005,4(6): 300 -311.
[2]Nykolak G,Raybon G,Mikkelsen B,et al.A 160 Gb/s free space transmission link[C]∥Optical Wireless Communications III.Bellingham: SPIE,2001: 4214,11 -13.
[3]Smutny B,Kaempfner H,Muehlnikel G,et al.5.6 Gbps optical intersatellite communication link[C]∥Free-Space Laser Communication Technologies XXI.Bellingham: SPIE,2009,7199:1 -8.
[4]Nakazawa M,Yamamoto T,Tamura K R.1.28 Tbit/s-70 km OTDM transmission using third and four-order simultaneous dispersion with a phase modulator[J].Electron Letter,2000,36(24):2027 -2029.
[5]Liu C H,Yeh K C.Propagation of pulsed beam waves through turbulence,cloud,rain,or fog[J].J Opt Soc Am,1977,67(9):1261 -1266.
[6]Liu C H,Yeh K C.Pulse spreading and wandering in random media[J].Radio Science,1979,14(5): 925 -931.
[7]Kelly D E,Young C Y,Andrews L C.Temporal broadening of ultrashort space-time Gaussian pulses with applications in laser satellite communication[C]∥Free Space Laser Communication Technologies X.Bellingham: SPIE,1998,3266: 231 -240.
[8]Kelly D E T T S,Andrews L C.Temporal broadening and scintillations of ultrashort optical pulses[J].Waves Random Media,1999,9(3): 307 -325.
[9]Howlader M K,Jung J.Intersymbol interference due to the atmospheric turbulence for free-space optical communication system[C]∥IEEE International Conference on Communication.UK: IEEE Proc,2007: 5046 -5051.
[10]Feng T,Chen G,Fang Z.Multipath dispersion of pulse signals in a non-line-of-sight optical scattering channel[J].Chinese Optics Letters,2006,4(11): 633 -635.
[11]王佳,俞信.自由空间光通信系统中光脉冲展宽问题的研究[J].光学技术,2009,35(1): 80 -83.WANG Jia,YN Xin.The research of pulse stretch in free-space optical communication[J].Optical Technique,2009,35(1):80 -83.(in Chinese)
[12]陈纯毅,杨华民,姜会林,等.激光脉冲云层传输时间扩展与信道均衡[J].兵工学报,2008,29(11): 1325 -1329.CHEN Chun-yi,YANG Hua-min,JIANG Hui-lin,et al.Temporal dispersion of laser pulse through clounds and channel equalization[J].Acta Armamentarii,2008,29(11): 1325 -1329.(in Chinese)
[13]韩燕,强希文,冯建伟,等.大气折射率高度分布模型及其应用[J].红外与激光工程,2009,38(2): 267 -271.HAN Yan,QIANG Xi-wen,FENG Jian-wei,et at.Height distribution profiles and its application of atmosphere refractive index[J].Infrared and laser Engineering,2009,38(2): 267 -271.(in Chinese)
[14]Gibbins C J.Propagation of very short pulses through the absorptive and dispersive atmosphere[J].Proc Inst Elect Eng,1990,137(5):304 -310.
[15]Owens J C.Optical refractive index of air: Dependence on pressure,temperature and composition[J].Applied Optics,1967,6(1): 51 -59.
[16]Marcuse D.Pulse distortion in single-mode fibers.3: chirped pulses[J].Applied Optics,1981,20(20): 3573 -3579.
[17]Agrawal G P.非线性光纤光学原理及应用[M].第3 版.北京: 电子工业出版社,2005: 53 -60.Agrawal G P.Nonlinear Fiber optics & application of nonlinear fiber optics[M].3rd ed.Beijing: Publishing House of Electronics Industry,2005: 53 -60.(in Chinese)
