切向超声振动辅助磨削对单颗粒切削力的影响
2011-02-22张洪丽张建华
张洪丽,张建华
(1.山东交通学院 机械系,山东 济南250023; 2.山东大学 机械工程学院,山东 济南250061)
在磨削过程中,磨削力的大小不但可以反映出整个磨削过程中砂轮与工件之间的相互干涉过程,评价磨削效果的好坏,还可以在一定程度上预测加工表面质量及加工变质层深度[1-2]。超声振动辅助磨削过程中,工件的切向超声振动改变了工具工件间的相对运动过程,进而引起磨削力的变化[3]。目前对超声振动辅助磨削力的研究多基于具体条件下的试验性分析,缺乏通用性。因此,有必要对超声振动辅助磨削力进行理论分析,建立加工过程中磨削力的数学模型,分析各因素对磨削力的影响。这是进一步揭示磨削机理、合理解释磨削中的各种物理现象,以及选择适当磨削用量的前提条件。本文主要对切向超声振动辅助磨削单颗粒切削力进行分析,建立其数学模型,该分析结果对优化硬脆性材料加工参数、改善其加工质量有重要的理论价值和实际意义。
1 研究对象
如图1所示,工件以进给速度vw水平运动,同时以超声振动频率f( 16~25 kHz)和振幅A( 4~10 μm)沿砂轮的切向超声振动; 砂轮直径为ds,以圆周速度vs作等速圆周运动。

图1 切向超声振动辅助磨削Fig.1 Tangential ultrasonic vibration assisted grinding
对研究对象及切削过程作以下假设[4]:
1)砂轮表面各磨粒沿同一圆周等距分布;
2)加工工件材料各向同性,加工过程中被切除材料全部以切屑方式去除;
3)超声振动在加工过程中保持稳定状态,即振幅、频率保持不变。
2 单颗粒切削力研究
2.1 单颗粒切削深度
图2中,O1为t 时刻前一磨粒切削至C 点时,砂轮中心的位置; O'1为t'时刻前一磨粒切削至A点时,砂轮中心的位置,O'1A=ds/2.O2为t 时刻后续磨粒切刃切削至B 点时,砂轮中心的位置,O2B=ds/2.AB 线段长度为单颗粒在t 时刻的切削深度atgt.
根据图2所示几何关系,推导单颗粒在净磨削时间区间内的动态磨削深度为

取加工参数a=1 mm,vw=400 mm/min,vs=18.3 m/s,A=0.004 mm,f=20 kHz,ds=50 mm 时,普通磨削和切向超声振动辅助磨削过程中,单颗粒切削深度agt和atgt随时间的变化曲线,如图3所示。由图3可以看出,切向超声振动辅助磨削时,单颗粒的切削深度断续变化,而且远大于普通磨削时的切削深度。

图2 单颗粒切削深度Fig.2 Cutting depth of single abrasive grit
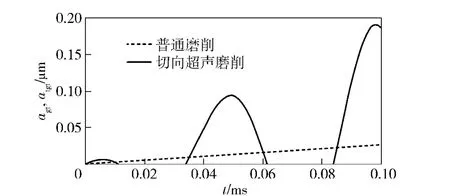
图3 单颗磨粒切深随时间t 的变化曲线Fig.3 Cutting depth vs.time
实际加工过程中,t 与t'差值很小,为计算方便,可用下式计算atgt,

式中:O1O2=avw/vs+2Acos( ωt+aω/2vs)sin ( aω/2vs);t'1、t2分别为一个周期内,磨粒切出和切入工件的时刻,根据切向超声振动辅助磨削运动学分析确定。
切向超声振动辅助磨削和普通磨削下单颗粒切削深度比值为
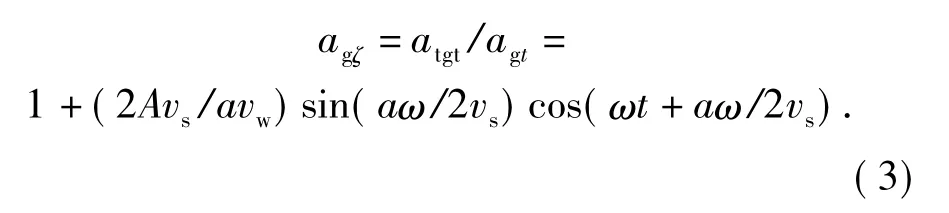
根据切向超声振动辅助磨削运动学分析,令
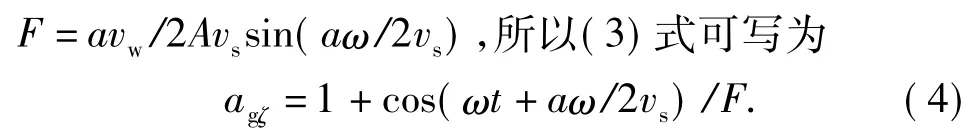
由于切向超声振动辅助磨削单颗粒切削过程的分离特性,一个振动磨削周期T 内,单颗粒平均切削深度比值为

根据上述分析,切向超声磨削过程中单颗粒的平均切削深度为

2.2 单颗粒切削力数学模型的建立
根据切向超声振动辅助磨削运动学分析[5-6],单颗粒在切削过程中具有分离特性,切削轨迹近似为正弦曲线。单颗粒在切削过程中的受力情况,如图4所示。其中,dFtg0为作用在磨粒锥面上微小面积( 和图4( a)中阴影部分对应的锥面积)ds 上的切削力,dFtg0t为该切削力的切向力分量,dFtg0n为该切削力的径向力分量。

图4 单颗粒磨削力计算模型Fig.4 Force model of single abrasive grit
根据普通磨削单颗粒受力理论模型[1],切向超声振动辅助磨削过程中,对微小面积ds 上的切削力分量dFtg0t和dFtg0n进行积分计算,求得在t 时刻作用在单颗粒上的磨削力为

式中:ρtst=atgt/cosδ,δ 为磨粒半定锥角;Ftu为切向超声振动辅助磨削单位磨削力;Ftgt为切向超声振动辅助磨削t 时刻作用在单颗粒上的切向磨削分力;Ftgn为切向超声振动辅助磨削t 时刻作用在单颗粒上的径向磨削分力。因而可得

由图4( b)可以看出,由于切向超声振动辅助磨削具有分离特性,单颗粒在磨削过程中受脉冲力作用。
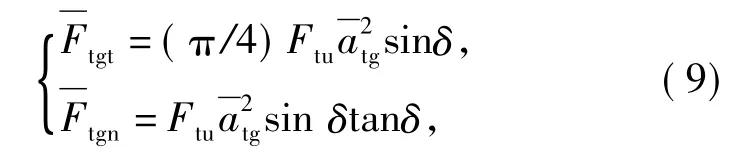
于是可得磨削力的计算公式

式中:Nd为磨削区内动态有效磨刃数;为切向超声振动辅助磨削切向平均磨削力;切向超声振动辅助磨削法向平均磨削力。
3 切向超声超声振动辅助磨削力试验
3.1 试验装置及方案
试验在ACE-V500 立式加工中心上进行,主轴最高转速为9 000 r/min;CSF27 型超声发生器,最大输出功率为150 W; KISTLER 9257A 型三向压电晶体测力仪、电荷放大器、AZ208R 采集板等测量磨削力,磨削力信号使用CRAS V6.1 信号采集与分析系统软件进行处理; 试验前测定超声振动幅值A 为5 μm;示波器测定超声振动频率f 为20.8 Hz.金属结合剂CBN 砂轮,粒度140#,浓度100%,直径50 mm.试验材料为烧结NdFeB 永磁体材料,其性能如表1所示。
试验工装系统如图5所示。试验过程中,打开超声波发生器为超声振动辅助磨削,关闭超声波发生器则为普通磨削。为了保证数据的正确性,每次试验进行3 次,取其平均值。

表1 烧结NdFeB 永磁体材料性能Tab.1 Performance parameters of sintered NdFeB material

图5 工装系统图Fig.5 Tools system
采用正交试验法测定磨削用量对磨削力的影响。试验加工因素水平如表2所示。
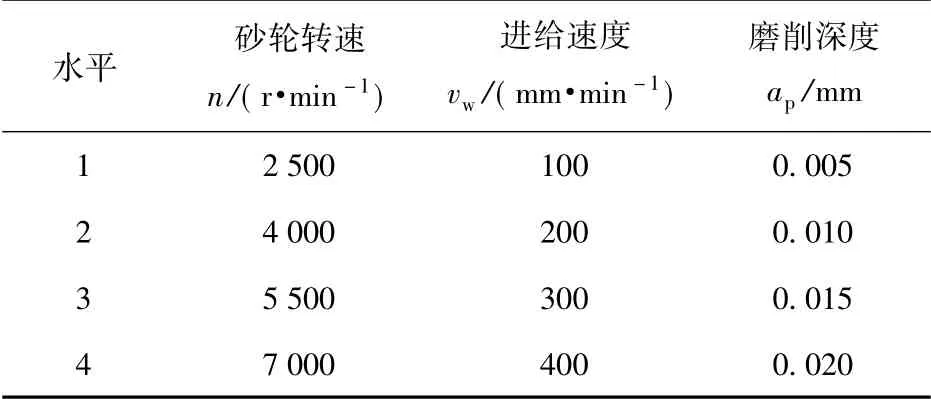
表2 试验加工因素水平表Tab.2 Test factors and levels
3.2 试验结果分析
图6给出了普通磨削和切向超声振动辅助磨削2 种加工方式下,切向磨削力Ft和法向磨削力Fn随磨削深度ap变化的关系曲线。可以看出,在2 种加工方式下,随着磨削深度的增加,切向磨削力Ft和法向磨削力Fn基本呈上升的趋势。这是因为增大ap会使磨粒切削厚度增加,同时又使磨削弧长增大,有效磨粒总数增多,因此磨削深度的增加使磨削力增大。
图7给出了普通磨削和切向超声振动辅助磨削2 种加工方式下,切向磨削力Ft和法向磨削力Fn随工件速度vw变化的关系曲线。可以看出,在2 种加工方式下,随着工件速度的提高,切向磨削力Ft和法向磨削力Fn基本呈上升的趋势。由于工件进给速度变化范围较小,因而磨削力上升趋势不明显。只有无超声振动时的法向磨削力随着工件速度的增加急剧上升,这是因为工件速度增大,单颗粒切削深度增加,导致磨粒切入工件更加困难。

图6 2 种加工方式下磨削深度对磨削分力的影响Fig.6 Effect of ap on grinding force in CG and TUAG
图8给出了普通磨削和切向超声振动辅助磨削2 种加工方式下,切向磨削力Ft和法向磨削力Fn随砂轮速度vs变化的关系曲线。可以看出,在2 种加工方式下,随着砂轮速度的提高,切向磨削力Ft和法向磨削力Fn基本呈下降的趋势。这是因为砂轮速度提高,磨粒切削深度减小,磨削力下降。
3.3 磨削力仿真
取与试验相同的加工参数,根据建立的磨削力数学模型,用MATLAB 软件对磨削深度、工件速度及砂轮速度等磨削用量对普通磨削和切向超声振动辅助磨削加工磨削力的影响进行仿真,仿真结果如图9~图11所示。将图9~图11分别与图6~图8进行比较可以看出,仿真所得磨削力随各磨削用量的变化趋势与试验结果基本一致。然而,相同加工条件下,仿真所得磨削力数值小于试验数值。这是因为实际加工过程中存在摩擦力,并且加工过程中各种不确定因素的影响导致实际磨削力大于理论计算值。

图7 2 种加工方式下工件速度对磨削力的影响Fig.7 Effects of vw on grinding force in CG and TUAG

图8 2 种加工方式下工件速度对磨削力的影响Fig.8 Effects of vs on grinding force in CG and TUAG

图9 2 种加工方式下磨削深度和磨削力的仿真曲线Fig.9 Simulation results of ap and grinding force in CG and TUAG

图10 2 种加工方式下工件速度和磨削力的仿真曲线Fig.10 Simulationresults of vw and grinding force in CG and TUAG

图11 2 种加工方式下砂轮速度和磨削力的仿真曲线Fig.11 Simulation resulta of vs and grinding force in CG and TUAG
4 结论
根据对切向超声振动辅助磨削加工过程中磨削力的理论分析及试验研究得出:在相同加工条件下,由于切向超声振动的引入,加工过程中单颗粒的切削深度呈断续变化且远大于普通磨削时的切削深度,单位磨削力低于普通磨削;切向超声振动辅助磨削过程中,切向磨削力比普通磨削的低,法向磨削力比普通磨削的高,因而切向超声振动辅助磨削的磨削力比远远低于普通磨削的磨削力比,这表明超声振动的引入可以在很大程度上改善工件材料的可磨削性;仿真所得磨削力随各磨削用量的变化趋势与试验结果基本一致,进一步证明切向超声振动辅助磨削力数学模型的正确性。
References)
[1] 郑善良.磨削基础[M].上海:上海科学技术出版社,1988.ZHEN Shan-liang.Basic theory of grinding[M].Shanghai:Shanghai Science & Technology Press,1988.( in Chinese)
[2] 贺永,董海,马勇,等.工程陶瓷磨削力的研究现状与进展[J].金刚石与磨料磨具工程,2002,127(1):40-44.HE Yong,DONG Hai,MA Yong,et al.Research status and progress of the grinding forces during ceramics grinding[J].Diamond& Abrasives Engineering,2002,127 (1):40-44.( in Chinese)
[3] Zhao B,Wu Y,Liu C S,et al.The study on ductile removal mechanisms of ultrasonic vibration grinding Nano-ZrO2ceramics[J].Key Engineering Materials,2006: 304-305,171-175.
[4] Li K,Warren L T.Modeling of ceramic grinding processes-partⅠ:number of cutting points and grinding forces per grit[J].Journal of Materials Processing Technology,1997,(65):1-10.
[5] 张洪丽,张建华.超声振动磨削运动学分析[J].制造技术与机床,2006,(6):63-66.ZHANG Hong-li,ZHANG Jian-hua.Kinematics analysis on ultrasonic vibration grinding[J].Manufacturing Technology&Machine Tool,2006,(6):63-66.( in Chinese)
[6] Feng B F,Cai G Q,Sun X L.Groove,chip and force formation in single grain high-speed grinding[J].Key Engineering Materials,2006,304/305:196-200.
