一般Lurie 系统的绝对稳定的新结果

赵秀元

(榆林学院数学与应用数学系， 陕西 榆林 719000)

0 引 言

关于Lurie 系统绝对稳定性的研究已经有许多研究结果[1-10].文献[11]通过界定非线性项的方法[12]，把Lurie 系统看成一个线性不确定系统，进而把Lurie 系统的绝对稳定性问题等价为具有不确定项的线性系统的鲁棒稳定性问题.

在研究鲁棒稳定性时，不确定系统通常重排成如图1所示的PΔ-结构，其中，P(s)是正规线性系统，Δ表示不确定扰动.

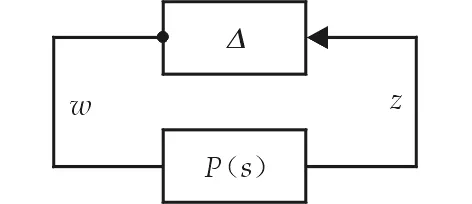
图1 稳定性分析框架

在分析Lurie系统绝对稳定性的情况下，Δ被进一步表示为模有界的块对角矩阵.本文利用文献[11]的方法，将Lurie 系统绝对稳定性的结果推广到一般Lurie 系统和具有重叠非线性项的一般Lurie 系统.

1 预备知识

文献[11]用实结构奇异值分析方法研究了如下Lurie系统的绝对稳定性

这里x∈Rn是状态向量；u∈Rp是输入向量；y∈Rp是输出向量；{A,B,C}是最小实现；Φ:Rp→Rp是时不变无记忆非线性项，它的元素φi:R→R是全局Lipshitz函数.

假设φi是满足下列3个条件之一的一、三象限非线性函数：

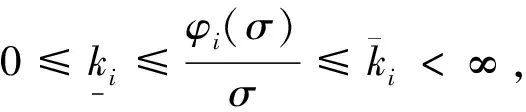
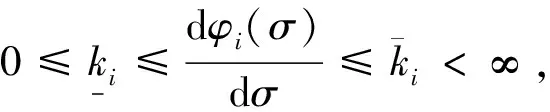
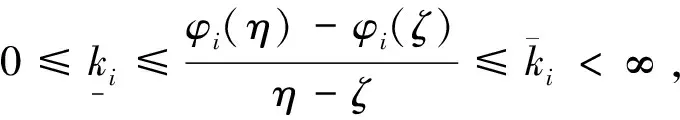
先介绍文献[11]的一个定义和两个引理：

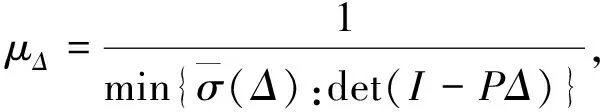
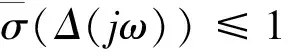
φi(σ)=(mi+δiλi)σ且|δi|≤1

引理2[11]定义的Φ(y)的均值增益为矩阵M=diag{m1,m2,…,mp}，Φ(y)的扰动界为矩阵A=diag{λ1,λ2,…,λp}和Δ=diag{δ1,δ2,…,δp}，则非线性Φ(y)项可表示为

Φ(y)=(M+ΔΛ)y, -I≤Δ≤I

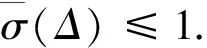
2 主要结果

本文考虑多变元一般Lurie系统

(1)

{A,B,C,D}是最小实现.

由引理1，把系统(1)化为

(2)

令E=[I+D(M+ΔΛ)]-1C，z=AEx，w=Δz，则得到PΔ-结构.

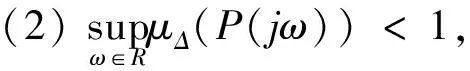
这里P(s)表示的状态空间是

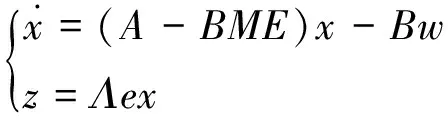
(3)

接下来考虑多变元一般Lurie重叠非线性系统

(4)

这里x∈Rn是状态向量，A∈Rn×n，B∈Rn×p，F∈Rp×n，G∈Rp×q，C∈Rq×n，D∈Rq×q，函数Φ1:Rp→Rp，Φ2:Rq→Rq是时不变无记忆非线性项，它的性质同前面的函数一样.

非线性项Φ1(y)和Φ2(v)表示为Φ1(ξ)=(M1+Δ1Λ1)ξ, -I≤Δ1≤I,Φ2(σ)=(M2+Δ2Λ2)σ,

-I≤Δ2≤I.

由引理1，把系统(4)化为

(5)

这里E=[I+D(M2+Δ2Λ2)]-1C，于是可得如下系统

(6)

定义新的变元z=ΛEx，w1=Δ1Λ1Fx，w2=Δ2Λ2Ex，w3=Δ1Λ1GM2Ex，w2=Δ1Λ1Gw2，则得到PΔ-结构.

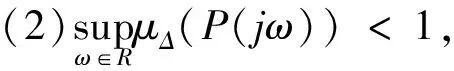
这里表示P(s)的状态空间是

(7)

3 结束语

本文研究了一般Lurie 系统的绝对稳定性,给出了一个新的结果，同时研究了具有重叠重叠非线性项的一般Lurie 系统的稳定性问题,把文献[11]的结果推广到了一般Lurie 系统和具有重叠非线性项的一般Lurie 系统.

参考文献

[1] 谢惠民.绝对稳定性理论与应用[M]. 北京：科学出版社, 1986.

[2] 廖晓昕.稳定性的理论、方法和应用[M]. 武汉：华中理工大学出版社,1999.

[3] H. K. Khalil. Nonlinear Systems, Macmillan[M].New York, 1992.

[4] W.M. Haddad, V.Kapila. Absolute stability criteria for multiple slope-restricted monotonic nonlinearities[J].IEEE Trans.Automat. Control，1995，40(2)：361-365.

[5] Z.X. Gan, W.G. Ge.Absolute stability of general Lurie systems with multi-nonlinear feedback terms[J].Acta Mathematica Sinica, 2001，17(4)：649-656.

[6] Z.X. Gan, J.Q. Han. Lyapunov function of general Lurie systems with multiple nonlinearites[J].Applied Mathematics Letters, 2003，16(1)：119-126.

[7] Z.X. Gan, W.G. Ge, S.X. Zhao.Absolute stability of general Lurie type indirect control systems[J].Acta Mathematica Applicatae Sinica, 2001，17(1) ：81-85.

[8] 甘作新, 韩京清，葛渭高.具有多个非线性项的一般Lurie直接控制系统的绝对稳定性[J].数学学报,2002， 45(2)：405-410.

[9] 杨 斌，潘德惠.具有重叠非线性元素的时变控制系统的绝对稳定性[J].辽宁师范大学学报， 1998，21(3)：195-197.

[10] 赵秀元.具有重叠非线性项的一般Lurie系统的绝对稳定性[J].大学数学, 2010，26(6)：53-57.

[11] C.H. Lee, J.C.Juang. A novel approach stability analysis of multivariable Lurie systems[J]. Applied Mathematics Letters, Proc. of the IEEE International Conference on Mechatronics & Automation, Niagara Falls, Canada, 2005,(6)：199-203.

[12] J. C. Doyle.Analysis of feedback systems with structured uncertainty[J].IEE Proc.，1982，129(6)：242-250.