存在不同取货频次情况的汽车生产配送物流研究
2011-02-20季建华
柴 轶, 季建华, 孙 琦
(上海交通大学安泰经济与管理学院, 上海 200030 )
0 引 言
汽车物流业一直以来都被国际物流同行公认为最复杂、最专业的物流领域.作为从事汽车物流服务的第三方物流企业,如何利用自身资源,更好地开展物流业务,高效地满足企业生产及物资流通的需要,降低物流成本,从而增强我国汽车制造企业及其产品在国内外市场的竞争能力,是一项非常具有现实意义的研究课题.
汽车制造企业的生产工序复杂、技术含量较高,一辆汽车的生产组装需要上万个零配件和百十余种原材料,因此,生产物流是涉及企业核心技术的非常重要、非常复杂、专业性很高的物流系统[1].在目前的汽车生产中,生产物流居于很重要的地位.物流服务供应商必须将原材料在特定的时间运送到主机厂以供主机按计划生产[2,3].但是在实际的企业运作中,物流服务提供商却面临以下几个问题:
(1)运输成本最小化.在实际运输过程中,企业为节省成本,往往采用milk-run的形式进行运输,由于供应商众多,运输问题即为NP-HARD问题[4],在运输过程中,如何有效的压缩成本就成为了第三方物流商面临的一个难题.
(2)运输频次不一致[5].由于汽车制造过程中所需要的原材料和零部件非常复杂,所以主机厂对其所需要的频次也存在着非常不一致的情况.有些零部件必须达到一日一运输的频率才可以保证生产顺利,而有些零部件体积很小且使用频度不高,在这种情况下再进行每日取货显然很不经济[6].本研究针对汽车物流中不同频次的配送点展开研究,希望结合定量分析及软件计算等方法,验证不同频次配送点组合的可优化空间.
1 汽车生产物流优化模型构建
1.1 模型假设及变量定义
k:完成配送所需要的车辆数,T0:每辆车每天可以工作的时间,T1:每辆车在RDC中的装卸时间,Q:车辆可以运送的最大载货量,v:车辆运输的速度.
1.2 模型构建
如果把RDC和供应商用顶点表示,它们之间的距离看成是边,边长已知,这样就得到了一个满足三角不等式的完全图,于是这个问题就转化为一个完全图分解成若干个子图的问题.这里的每个子图被称为子环游[7],要求这些自环游中的任意两个有且只有一个公共顶点(也就是备件RDC),它们能覆盖图的全部顶点,如图1所示.
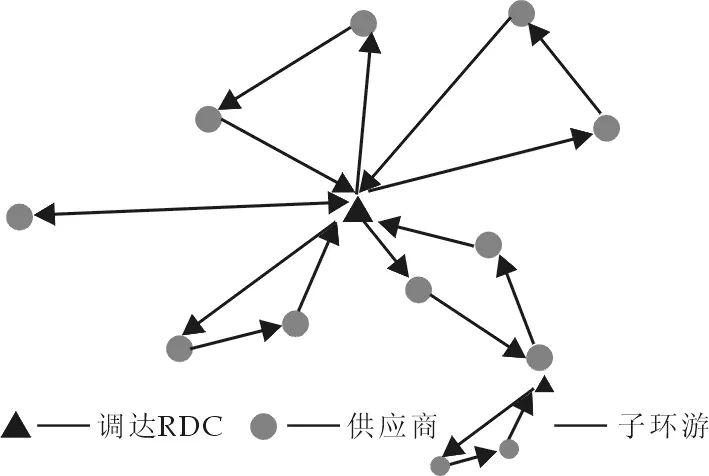
图1 物流网络配送示意图
由定义1,可以建立模型2:
mink
(1)
S.T.E(Ci)/v+Z[(V(Ci)
(2)
[V(Ci)∩V(Cj)]
(3)
(4)
D[V(Ci)]≤Q
(5)
其中:(1)表示优化目标,配送需要的车辆最少,也就是子环游的个数最小;(2)指每辆车的配送时间不能超过T0个小时,Z[(V(Ci)
1.3 配送频次方案组合
根据汽车生产物流实际运作模式及货量大小,现假设供应商取货的频率可以归结为一天一次,两天一次,一周两次和一周一次这4种情况[8,9],为了方便表示,可以用①②③④来表示每一类供应商,具体含义如表1.

表1 符号含义
供应商的不同频次势必会影响配送路线和配送计划,项目具体的解决方法可通过下面的说明解释.
根据现有的工作模式,不妨以周一作为循环开始,以一星期为一循环(6个工作日),每天取货的供应商根据供应商的取货频次不同进行组合.为了方便解释,不妨假设只存在每天取货一次的情况及每两天配送一次的情况,即只存在①和②两种情况,先将①和②组合,如表2所示.
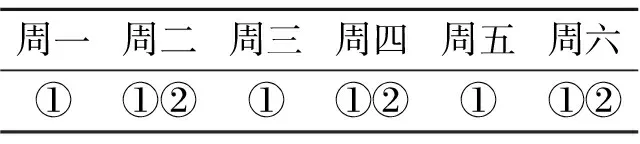
表2 ①②的组合结果1
表2表示,在只负责运输第一类及第二类供应商的情况下,周一只用负责第一类的取货,而周二就需要同时负责第一类及第二类的取货.但是,还有另外一种配送方案,如表3所示.

表3 ①②的组合结果2
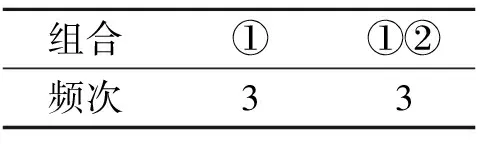
表4 ①和②不同组合出现的频次
但无论何种配送方案,从表2、表3可以看出不同组合出现的频次均相同,如表4所示.
由此可以看出,如果每周只负责运输第一类及第二类供应商的话,一周6天的工作日中,需要有3天对第一类的供应商配送,3天对第一类及第二类统一配送.
在这个基础上,将第三类③加入,不管是加在哪一天,组合出现的频次均是不变的.不妨假设是第一种情况,结果如表5~表7所示.
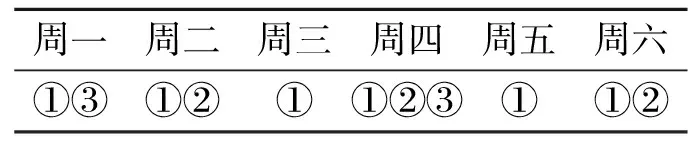
表5 第一、四天加入③

表6 第二、五天加入③

表7 第三、六天加入③

表8 ①、②、③组合出现的频次
从表5~表7可以看出,不同组合出现的频率如表8所示.
在表8的基础上,将第四类④加入,这时会出现不同的情况,不妨假设目前采用的配送方案是在一、四天加入③.在此基础上,可以推导出以下几种情况,如表9~表12所示.

表9 第一天加入④

表10 第二(六)天加入④

表11 第三(五)天加入④

表12 第四天加入④
现在把表9~表12表示的配送方案命名为方案一、方案二、方案三、方案四,表13表示4种方案下不同组合的频次情况.
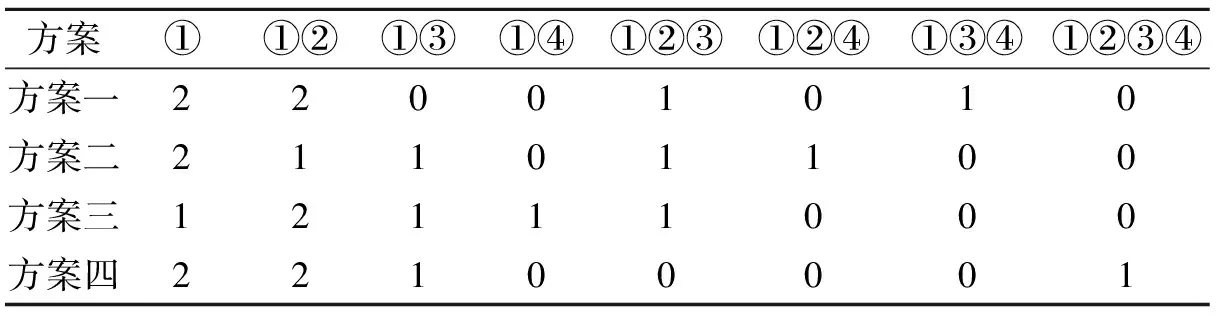
表13 不同组合及相应的频率
基于以上分析,可以看出,配送成果是跟具体选择的方案挂钩的,为了得到最优的配送方案,计算过程中需要将4种优化方案加以比较,从中选择最优方案.
2 模型运算
2.1 模型赋值
Q=40,表示每辆车最大容积是40 m3;T0=10,表示每辆车每天的工作时间不超过10 h;T1=1,表示每辆车每天需准备1 h装卸货时间;v=50,表示车辆速度为50 km/h.
本次运算采用25个配送点,其相互之间距离见附表.为方便计算,每个点的货量设为15.
2.2 软件编写
本项目中所面临运输路线优化问题是一个NP-HARD问题,是算法领域具有一定难度的问题,在学术界目前没有公认的最优解决方法,只可以利用启发式算法加以优化.目前在算法方面,比较普遍采用的有遗传算法、蚁群算法、模拟退火算法等[10].本文运算程序采用C#编写,采用领域搜索算法进行编写,经测试,运算结果令人满意.
2.3 计算结果

表14 运算结果情况
软件运行结果如表14所示.
由表14得知4个方案运行结果如表15所示.

表15 各个方案运行成本情况
由此可知,方案三在所有4个方案中成本最低.由此可见,不同的排列组合对企业的运输成本有着较大的影响.优化过程中,4类方案的优劣并不能一目了然,需要结合实际数据加以测算.在实际企业运作过程中,企业的配送点会更加复杂,为后期的优化提供了更大的优化空间.
3 结 论
在实际情况中,供应商取货的频次往往存在很大差别.经过不同配送频次之间的组合往往可以得出不同的配送方案,而不同的方案往往会根据供应商之间距离不同产生成本上的差异.在已知配送频次所需不同的情况下,如果可以有选择地根据计算结果来进行配送路线设计及配送,则可以有效降低供应商取货的成本.在此基础上,为供应商取货管理提供了可能性及理论基础.
从结果中可以看出,4种方案的优劣并不能直接看出,要结合实际运作情况中具体取货点之间的距离来确定.在实际运作情况中,由于存在着取货量不一的情况,取货的情况会更加复杂,所以有必要采取计算机计算的方式来确定最终配送路线.此问题为NP-hard问题,有多种算法可供选择,本文选择的领域搜索方法效果良好.本文研究的管理意义如下:
(1)在存在多种供应商且各个供应商配送频次不一致的情况下,可以根据其频次进行不同组合,结合供应商之间的距离进行优化,根据成本最低原则对供应商取货具体日期进行管理,从而降低成本.
(2)在实际运输情况中,通过配送频次的优化组合,不仅可以降低车辆milk-run过程中的直接运输成本,而且可以有效提高车辆的满载率,提高运输效率,从而产生进一步的优化空间.
(3)配送频次的最优组合一旦确定,即可作为最优配送路线的选择及各类配送中心确定的数据基础,为运输企业提供管理支持.
参考文献
[1] 蓝青松,徐广卿.从传统运输迈向现代物流——入厂物流的“循环取货”管理模式[J].现代物流,2004,(1):18-20.
[2] 周正蒿. 汽车零部件物流运输系统设计[J]. 物流与交通, 2005 (1):13-16.
[3]方春明,孔繁森,隽志才.汽车工业供应物流配送中心选址研究[J]. 公路交通科技,2009,26(6):142-146.
[4] Maria Anne Skaates, Veikko Seppanen. Managing relationship-driben competence dynamics in professional service organizations[J]. European Management Journal,2002,20(4):430-437.
[5] 徐秋华.循环取货方式在上海通用汽车的应用[J].现代物流,2002,(3):35-37.
[6] 屈丽萍.国内汽车物流企业的现状及发展对策分析[J].物流技术,2005,(5):66-69.
[7] 邱伟星,沈金龙. 旅行商问题的一个近似算法[J].南京邮电学院学报,1998,18(1):106-108.
[8] 贺盛瑜,庞 宇.通用汽车物流运作模式实证研究[J].企业经济,2006,8(4):52-54.
[9] 刘 杰,李 丽.汽车制造业实施需环取货物流模式现状与展望[J].企业物流,2007,26(8):223-226.
[10] 刘云忠,宜慧玉.车辆路径问题的模型及算法研究综述[J].管理工程学报,2005,19(1):124-130.
