横掠紧凑叉排管束流动的数值模拟与分析

戴 伟，刘应征

DAI Wei，LIU Ying-zheng

（上海交通大学 机械与动力工程学院 动力机械及工程教育部重点实验室，上海 200240）

0 引言

横掠管束流动在工程上有着广泛的应用。锅炉中的省煤器，预热器，再热器以及核反应堆的燃料棒，甚至汽轮机和燃气轮机的刷式密封都可以看成是由管束流动系统。显然，了解不同布置形式的管束内部流场特征及压力损失水平与管束间距和雷诺数等参数之间的关系对相关工程应用很有帮助。针对横掠管束流动的数值模拟研究很多。潘维等人在2004年对管距s/d＝1.5～2的横掠管束流动进行了数值模拟，通过比较不同管束排列方式对气流的影响，得到叉排管束对流动的扰动比顺排管束更为强烈，且随着管束间距的增大，其扰动逐渐减弱。wang在2006年数值模拟了管距s/d=1.4的叉排管束流动，很好地预测了边界层分离点的位置。Liang 等人在2007年对管距s/d=1.6的叉排管束内部流动的涡脱落特性进行了大涡模拟，计算结果与激光多普勒实验测量结果吻合良好。Paul等人在2008年对大间距（s/d＝3.8）横掠管束湍流流动进行了实验和数值计算对比研究，发现k-e模型适用于周期性的空间流动，而k-w模型在发展区能更好地预测其平均速度。焦大鹏等人对管距s/d＝1.5的管束流动在不同排列形式下进行了数值模拟，获取了熵产数与雷诺数的变化关系，比较了它们热力学性能的优劣。以上文献研究表明，大部分的相关研究都集中在大间距管束流动，而对于紧凑布置的管束流动研究极少。仅M.J.Braun在1995年对紧凑布置的（s/d＝1.08）管束流动进行过数值模拟和实验验证，由于当时的计算条件所限，管束压力损失水平的计算误差最大达到了26%。

本文针对紧凑（s/d＝1.04，1.08和1.12）叉排管束流动进行了数值模拟，计算获取了四种雷诺数条件下（Re＝730，1460，2190，2920）其内部流态特征及压力损失水平。此处，雷诺数的定义为Re＝vsd/υ，vs为管束横向间距处的平均流速。计算结果表明，紧凑管束流动的压力损失水平与雷诺数成幂函数关系。此外，针对相同雷诺数（Re＝2920）下的三种不同间距管束流场的压力分布数值分析表明，随着管束间距的减小，其阻塞效果急剧增加，且小间距管束对雷诺数的增加非常敏感。

1 数学模型

本文所研究的主要是二维稳态横掠叉排管束流动，其流场主要受如下方程控制：

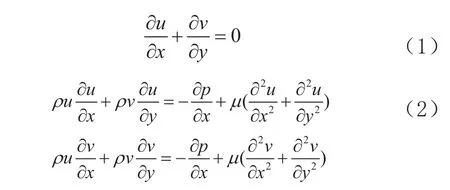
计算中，湍流模型采用标准k－ξ两方程模型，如（3）式所示。湍流模型中的系数GK为平均速度的梯度而产生的湍动能，C1τ和C2τ分别为常数1.44和1.92，ui＝ρCUk2/ε，CU为经验常数0.09。方程离散采用二阶迎风格式，压力和速度的耦合采用SIMPLE算法解耦。

本文计算模拟如图1所示布置的二维叉排管束流动，管径d为6.35mm。流向布置有6排管束，而在垂直来流方向的纵向布置有11排管束，以消除端壁影响。管束间距有三种工况，即S1/d＝S2/d＝1.12，1.08和1.04。计算中来流为均匀入流的速度入口边界条件，出口边界选择在下游距离最后一排管束约80倍d处，采用充分发展的出口边界条件。上下表面及管束外围均采用无滑移固定壁面条件，壁面附近采用标准壁面函数。

如图2所示为管束周围的网格分布。在管束区域计算采用非结构三角形网格，考虑到管束之间的间距较小，网格进行了加密处理。计算区域的网格总数约100万。

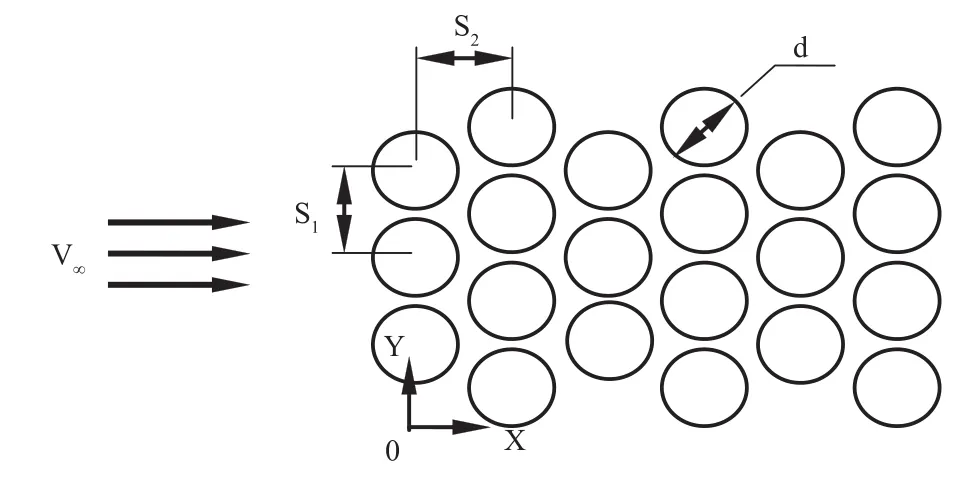
图1 紧凑叉排管束的排列方式示意图

2 计算结果及分析

如图3所示为横掠六排管束流动的速度矢量分布特征。由于管束之间的挤压作用，使得流体在管束间隙处获得了加速，高速流体在下游又撞击下一排的管束表面，出现分流。此外，靠近壁面的管束区域由于阻塞比较小，因此管束两侧的流速较中心区域的管束附近大。在靠近壁面的第二到第五排管束上下的流体分布并不对称，主流流体绕“s”形路线通过管束区域。在远离壁面的管束区域，流体在圆管上下的分布逐渐趋于对称。

图2 管束区域的网格

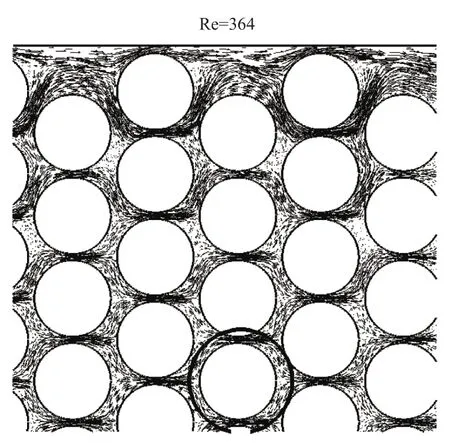
图3 横掠六排管束的速度矢量图

如图4（a）可见速度分量u的波动呈两头大，中间小的分布情形。中间部分的速度最大值为自由来流的2倍左右（2U），而在两端最大速度会增加到4U左右，在靠近壁面处出现了少量的回流，即速度为负值的情况，其大小为1U左右。这主要是因为此处流体在撞击下一排管束后，流体分布不对称，主流绕过管束以后会有少量流体继续沿着管束表面向上游回流。由图4（b）可以看出速度分量v的整体波动幅度基本不变，大概为8U。速度波动的中心轴线在两端处会由v/U＝0偏移至v/U＝±2左右。这表明，靠近两端处流体在撞击下一排管束后流速分配不再对称。

为了进一步对管束内的流场进行分析，研究紧凑管束对流体的扰动特性，如图5所示为第一、三排管束后的速度和压力分布情况。从速度分量v的分布曲线可以看出第一排与第三排管束后的速度分布曲线呈对称分布状态且进乎重合可以判断出对于紧凑排列的叉排管束，在经过第一排管束以后流场的速度分布已经稳定，不会像稀疏管束（s/d＞2）那样要经过四五排管束的作用，流场才趋于稳定[1]。另外，在速度分布曲线中可看出流体速度沿纵向上下波动较大。这主要是由于管束间距较小，流体在绕过管束流动的时候获得了较大的加速，使得在管束间隙与管束后沿的速度差较大，形成速度波动。虽然速度的绝对值上下波动较大，但其平均值的变化还是比较平缓的。由图中可以看出平均速度在纵向呈近似的抛物线分布，两端靠近壁面处的平均速度大于中间部分。这点变化特征还可以从压力p的分布中得到解释。如图4所示，中间部分的压力比两边大，从而形成由中间到两边的压力梯度，流体在压力梯度的作用下由中间向两边流动，增加了两端的平均速度。

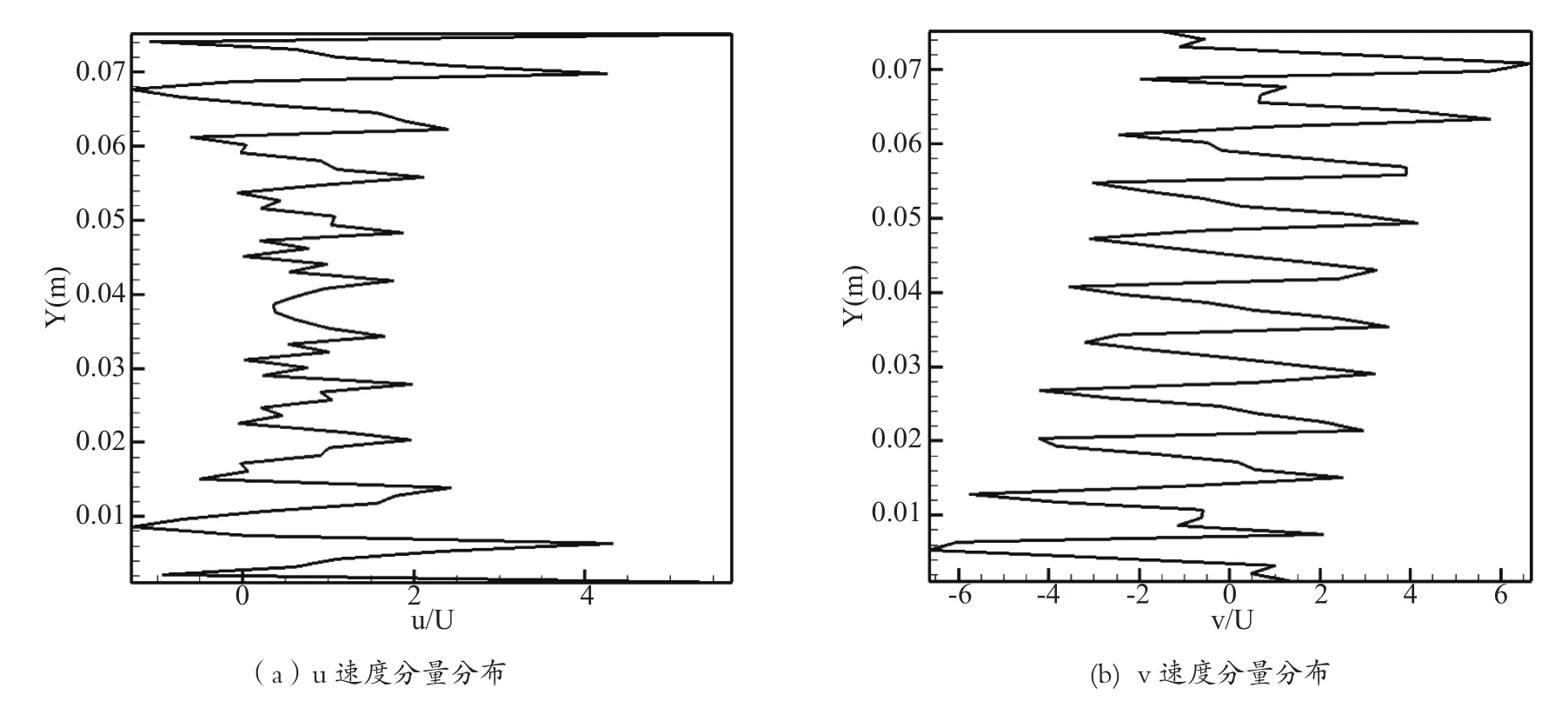
图4 管束区域x＝0.54d处各速度分量在y方向的分布曲线

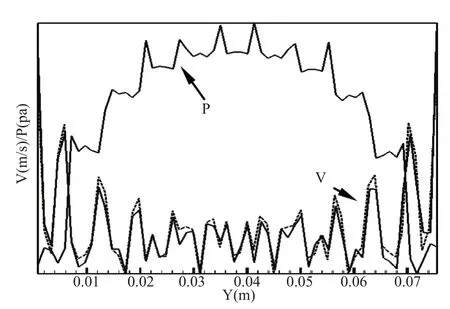
图5 第一三排管束后的速度分布曲线与第一排管束后的压力分布曲线

如图6所示为图三中黑色圆圈所标识圆管附近局部区域在三种不同雷诺数下的流线图。对于单个圆柱绕流而言，流体在管迎流面部分为顺压力梯度（dp/dx＜0），部分压能转化为动能，使流速增加，而在管束背面部分转为逆压力梯度（dp/dx＞0），压能回升使得动能减小，由于粘性损耗，在某点动能减小为零，就会发生边界层分离。在紧凑管束流动中，由于横向间距较小，使得管后部分的漩涡脱落受到抑制。由图所示在雷诺数为365时，管束后面流体仍贴着管束表面流动，上下游流线近似对称，并未发生流动分离。但当雷诺数为730时，在管束背面上部有对称的返向流动漩涡出现，当雷诺数达到1460时，管束背面上部的漩涡已比较明显。由于漩涡的出现阻塞了流动通道，使得两端压差增加。且漩涡越大其阻塞越严重，因此两端压差也将随雷诺数的增加明显上升。

如图7所示为三种管束间距（s/D=1.04，1.08和1.12）下的流动压力损失与雷诺数的关系。为简化计算，这里横向仅取中间三排，上下两侧取对称边界，结果如图7所示。随着雷诺数的增加，不同管束间距的管排两端压差都呈幂函数增长态势。但增加幅度并不一致，当s/d为1.12和1.08时，这两条曲线较为接近，且都与雷诺数的1.6次幂左右成正比。当s/d降低至1.04时，其增长幅度明显增加，经曲线拟合可知管束两端压差与雷诺数成1.77次幂函数关系。由此可见，小间距管束的两端压差对雷诺数的增加更为敏感。在Re=2920时，其压差达到了11.6Mpa，分别是其他两种几何情况的4.3倍和9.3倍。这表明，在紧凑排列条件下，随着管束间距的减小，在相同雷诺数下，其阻塞效果急剧增加。

3 结论

本文采用计算流体力学技术，对三种不同间距条件下（S1/d=S2/d=1.12，1.08和1.04）的二维紧凑叉排管束流动（Re=365～2920）进行了数值模拟和分析。计算结果表明：

1）对于管束间距s/d=1.08的紧凑叉排管束，在Re=365时，流体仍贴着管束外表面流动，上下游流线近似对称；当Re=730时，在管束背面上部出现了流动分离，有对称的返向流动漩涡出现；当Re=1460时，管束背面上部的漩涡已比较明显，漩涡的出现阻塞了流动通道，使得两端压差急剧增加。

2）对于紧凑排列的叉排管束，在经过第一排管束以后流场的速度的分布已经稳定，不会像稀疏管束（s/d＞2）那样要经过四五排管束的作用，流场才趋于稳定[1]，这是由于紧凑管束对流场扰动增强的结果。

3）在管束紧凑排列条件下，随着雷诺数的增加，两端压差呈幂函数增长趋势。当管束间距的减小到s/d=1.04，在相同雷诺数下，相对于其他两种大间距的情形而言，其阻塞效果非常显著。

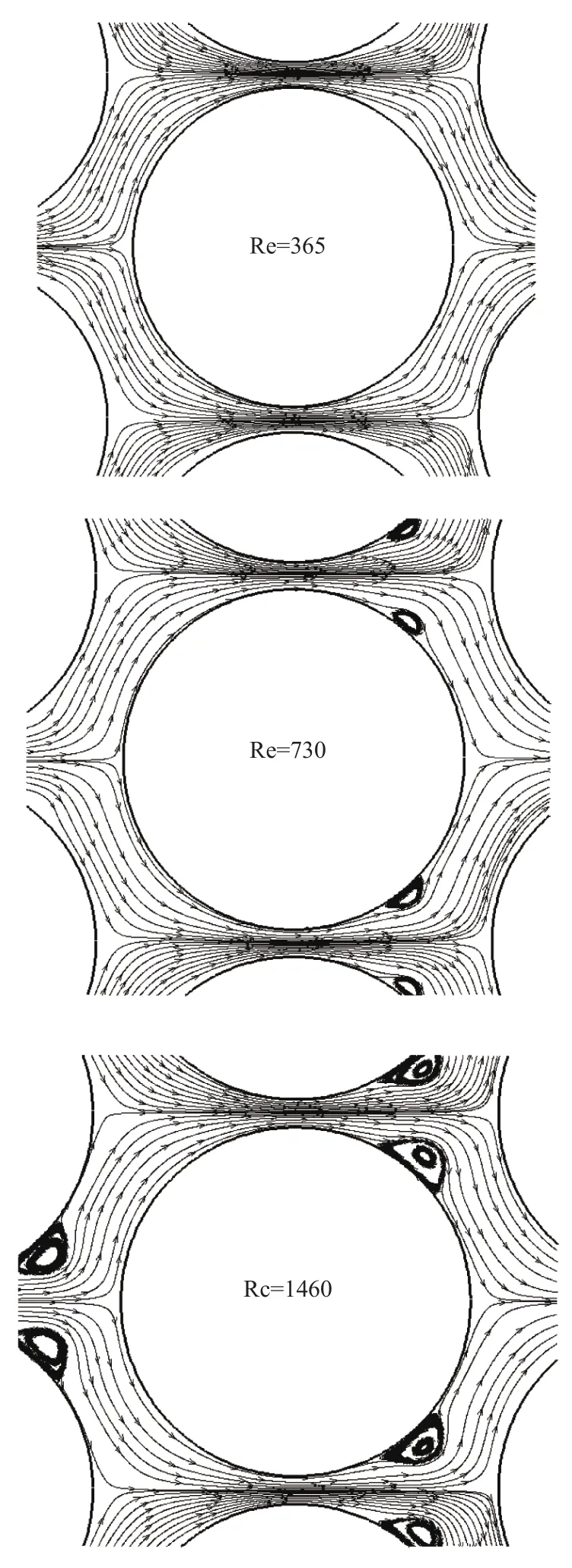
图6 不同雷诺数下叉排管束附近的流线图

图7 不同管束间距条件下两端压差随雷诺数的变化

[1]潘维,池作和,斯东波,岑可法.匀速流体横掠管束的流场数值模拟[J].浙江大学学报（工学版）,2004,38（8）：1043-1046.

[2]李大鹏,焦增庚,孙丰瑞.横掠不同型式光滑管束流动的热力学分析和比较[J].能源研究与信息,2002,18（2）：109-113.

[3]王秋红.换热器管束排列方式对流场的影响的数值分析[J].华北水利水电学院学报,2007,28（6）：45-47.

[4]杨记伟,滕丽娟,胥战海.多圆柱绕流漩涡脱落和流场形态概论[J].人民长江，2009,40（3）：66-69.

[5]黄杰,,王为民,,张德义,,王树立，非均匀来流绕流管束流动数值模拟[c].第十六届全国水动力学研讨会,2002,16.

[6]徐进良,吴履琛.沸腾并联管束多级节流下受热不均时流量分配计算模型研究[J].水动力学研究与进展 A辑，1993,8（12）：625-630.

[7]孙奉仲，张鸣远，黄新元，史月涛，董信光.镍基渗层纵向翅片管的强化传热试验研究[J].水动力学研究与进展A辑，2002,17（4）：467-471.

[8]程林.换热器内流体诱发振动[M].科学出版社，1995.

[9]M.J.Braun，V.V.Kudriavtseu.A Numerical Simulation of a Brush Seal Section and Some Experimental Results[J].Transactions of the ASME.1995，117：190-202.

[10]R.C.Hendricks，V.V.Kudriavtsev，M.J.Braun，M.M.Athavale.Flows in Pinned Arrays Simulating Brush Seals NASA Technical Memorandum 107333.

[11]S.S.paul，S.J.ormiston，M.F.Tachie.Experimental and numerical investigation of turbulent cross-flow in a staggered tube bundle[J].Heat and Fluid Flow 29（2008）387–414.