基于灰理论的成都市铁路旅客周转量预测
2011-02-15牟瑞芳
李 华, 牟瑞芳
( 西南交通大学 交通运输与物流学院,四川 成都 610031)
铁路是我国中长途旅客运输的骨干和中坚,2008 年全国铁路完成旅客周转量7 778 6000 万人·km,同比增长7.80%[1],但是21 世纪以来,随着汽车、航空运输的迅速发展,铁路不断受到新浪潮的冲击。成都是我国西南地区的交通运输枢纽,经过几十年的发展,交通运输结构发生了巨大变化,现已逐步形成了包括铁路、公路、航空并存的综合交通运输体系[2]。就铁路而言,目前成都铁路局运营有宝成铁路、成渝铁路、成昆铁路、遂渝铁路、襄渝铁路、川黔铁路、渝怀铁路、内昆铁路、黔桂铁路和沪昆铁路等干线及达成、达万、水柏线3 条合资铁路,11 条支线,营业里程超过5 000 km,承担着成都市超过54%的旅客周转量,再加上未来高速铁路、客运专线的迅速发展,铁路在整个成都市客运交通运输系统,尤其是中长途运输中仍占主导地位。
以成都市铁路运输为研究背景,对未来几年成都市铁路旅客周转量及其发展趋势进行预测,为合理组织规划高速铁路和客运专线提供数据参考,以达到提高成都市铁路运输经济效益和社会效益,满足国民经济迅速增长和人民生活水平日益提高的目的,对成都市未来铁路运输发展具有重要的现实意义。
1 预测方法综述
为了把握成都市未来铁路旅客运输的基本特征,对旅客周转量可采用多种方法进行预测,常用的预测模型有:逐步回归分析模型、BP 神经网络分析模型、灰色预测GM(1,1) 模型等。
逐步回归分析是应用多元回归分析方法建立回归方程对因变量进行预报、控制的一种回归分析法。回归方程中引入的变量都需要进行显著性检验,当引入的变量由于后续比变量的引入变得不显著则提出,直至无不显著变量从方程中剔除,又无显著变量引入。由于逐步回归分析自变量的多重共线性问题,分析结果不稳定,而且剔除的过程,可能使专业知识认定的显著因子落选,而且实际应用时,有些因子不能随意剔除,可见,逐步回归分析方法不太适应铁路客运周转量的建模需要。
BP 人工神经网络是20 世纪80 年代中后期出现的一种基于学习过程的建模方法。BP 神经网络的学习过程由正向传播和反向传播组成。传播过程中,对输入信号逐层处理,每一层神经元的状态只影响下一层。若输出层不能得到期望输出,则反向传播,同时返回输出误差。通过反馈的误差,修改各层神经元的权值,得到合适的网络连接值后,便可对新样本进行非线性映象。BP 人工神经网络存在局部极小问题,且当输入样本较多且具有多重共线性时,BP 神经网络会降低网络的训练速度和效率,影响预报精度。铁路客运周转量的原始数据相对其他训练模型来说相对较少,BP 人工神经网络不能有效的产生合适的模型,故该预测方法不太适用于铁路客运周转量的预测。
灰预测是灰色系统理论应用的重要组成部分,通常采用GM(1,1) 模型进行预测。灰预测[3]使用的不是原始数据,而是使用从原始数据累加或累减得到的AGO 或IAGO 序列,并通过级比检验验证模型的适用性,当预测模型建立后,还可通过残差检验进一步验证模型的适用性,当精度不理想时,可通过残差修正。灰系统模型预测克服了某些预测方法建模困难,计算工作量大[4]的缺点,允许在信息不完整的情况下,着眼于系统的灰色信息,寻求系统本身的内在规律,以期达到使灰系统白化的目的[5]。
但灰预测模型在数据量较大时的预测精度并不理想,仅适用于小规模平稳数据的近期预测,而且其模型中的指数因子决定了其只适用于类指数增长的数据序列的预测。由于影响旅客周转量的因子较多,长期预测结果精度很难得到保证,总体的数据量相对较小,因此,使用灰预测模型模型进行短期预测,将精度控制在理想范围之类。
根据成都市铁路发展趋势,基于当前高铁、客专影响因子的不完整性,采用灰预测模型对成都市铁路旅客周转量进行预测,预测特征年份推荐为2009 年、2010 年和2011 年。
2 灰预测模型建立
2.1 灰生成
灰预测[3]直接使用的不是原始数据,而是由原始数据层次变换的灰生成。层次变换灰生成分为累加生成AGO 和累减生成IAGO。

原始序列可能毫无规律可寻,累加后则易于找出规律,特别是当x(0)非负,其AGO 序列一定是递增的,这种递增特性具有显化内在规律的功能,有变不可比为可比的功能。
2.2 级比可容区检验

灰建模序列的级比σ( k) 必须落在可容区(0.135 3,7.389 0) 中,才能作GM(1,1) 建模,这是基本条件。
2.3 级比界区检验
为了获得精度较高的GM(1,1) 模型,级比σ( k) 应落入尽量靠近1 的子区间(1 - ε,1 + ε) 内,此子区间称为级比界区。
级比界区的计算公式

式中,n 是原始序列数据的数目。
2.4 数据处理方法
令x 为原始序列,ym为x 的m 次对数序列,则

2.5 GM(1,1)预测模型
令中间参数

则参数
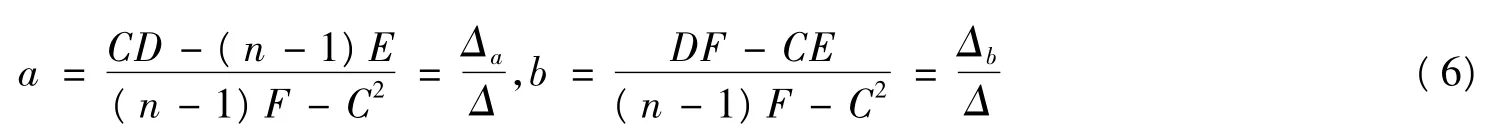
GM(1,1) 模型为

式中,x(0)是建模原始序列; x(1)是x(0)的AGO 序列; z(1)是x(1)的均值序列; a 为发展系数; b 为灰作用量。
2.6 灰预测模型检验
灰预测模型适用性判断通常通过两个步骤完成:对原始数列进行级比检验; 对预测值和原始数列进行残差检验。
残差相对值

平均残差

3 成都市铁路旅客周转量预测
使用GM(1,1) 模型进行预测的一般步骤:①原始数列级比可容区检验,建模可行性判断; ②原始数列级比界区检验,对级比界区检验不合格的序列,作数据变换处理;③GM(1,1) 建模;④预测值和原始数列残差检验;⑤对铁路旅客周转量作出预测。
根据以上步骤,选择2004—2008 年成都市铁路旅客周转量作为基础数据,数据来源于成都统计年鉴( 2008) ,见表1,对2009、2010、2011 年的铁路旅客周转量做预测。

表1 基础数据 万人·km
σ = ( σ(2) ,σ(3) ,σ(4) ,σ(5) = (0.898 095 27,0.912 581 7,0.928 971 47,0.899 969 38) ,σ ⊂(0.135 3,7.389 0) 。级比可容区检验通过,表明序列是平滑的,可做数列灰预测。
(3) GM(1,1) 建模。由式(5) 计算得C = 3.970 3 ×107,D = 1.485 6 ×107,E = 1.535 6 ×1014,F =4.627 2 ×1014。由式(6) 计算得a = -0.089 0,b =2.830 3 ×106,b/a = -3.179 5 ×107。由式(7) 得GM(1,1) 预测模型


GM(1,1) 预测结果见表2。
(4) 残差检验。由式(8) ,式(9) 得残差及残差相对值,见表3。
由式(10) 计算得平均残差
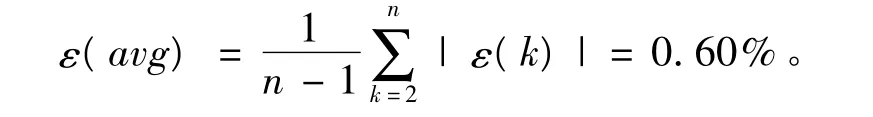

表2 灰预测铁路旅客周转量值 万人·km
GM(1,1) 拟合数列逼近原始数列,具有较高的残差检验精度,同时由模型精度检验等级[3]可认为该预测为高精度预测。
4 结语
从GM(1,1) 预测结果可以看出,2009 年至2011 年成都市铁路旅客周转量总体呈上升趋势,这也同当前高铁和客专大力发展的实际情况相符。GM(1,1) 预测值经过检验,预测结果精度较高,说明灰预测用作短期旅客周转量预测具有可靠性。
因模型自身的局限性和样本容量的有限性,再加上实际运用中,各种不确定因子的影响,未来铁路旅客周转量的预测值中需考虑一定的弹性范围,并在实际设计指标中予以体现。
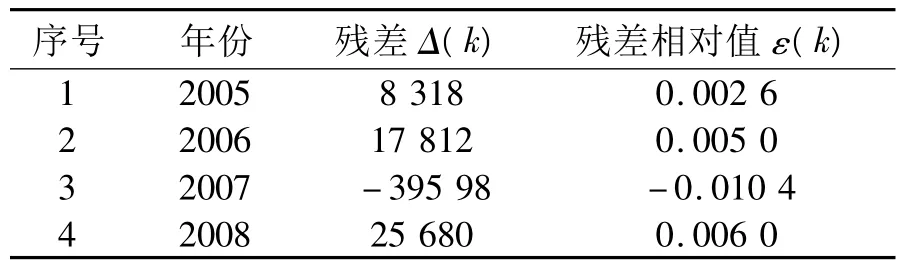
表3 预测值与原始数列残差检验结果
[1]铁道部统计中心.中华人民共和国铁道部2008 年铁道统计公报[J].中国铁路,2009(6) :3-9.
[2]霍娅敏,李德刚.成都市公路客运量预测[J].交通与安全,2005(11) :161-164.
[3]刘思峰,谢乃明.灰色系统理论及其应用[M].北京:科学出版社,2008.
[4]朱文婷,刘海林.基于灰色-马尔科夫链理论的公路客运量预测[J].交通科技与经济,2009(6) :12-17.
[5]纪跃芝,冯延辉,任有.公路客运量预测的数学方法[J].工业技术经济,1997,16(4) :81-84.
