基于模糊模式识别的金融数据分析

胡晓彤，王子银

（天津科技大学 计算机科学与信息工程学院，天津 300222）

0 引言

目前对于金融数据的分析，一般讨论的是金融市场的结构特点，文献[1]中讨论了金融市场的分形结构并进行了有效验证，但没有提出行之有效的对金融数据进行分析的方法。文献[2]中利用赫斯特指数对金融市场的循环周期以及转折点进行分析，但分析结果包含太多的主观因素，且仅由单一指标进行分析也使分析结果有很大的模糊性。本文通过分析金融市场中各种技术指标的特点，提出基于指标的协同作用分析金融市场中的数据模式，同时依据模糊模式识别理论对某一时刻的金融数据进行隶属度分析，得到该时刻数据隶属于某一模式类的强度，为金融数据分析提供数据支持。

1 金融市场指标协同作用下的数据模式

本文所研究的金融数据是指按照时间顺序排列的大量数据，如股票、外汇等的报价。目前，对上述数据的分析主要采用的指标包括布林带指标、相对强弱指标、移动平均线指标以及随机振荡指标等，通过分析上述几种指标的优缺点，本文将布林带指标、移动平均线指标以及随机振荡指标的分析结果予以综合，利用三者的协同作用以及与金融市场中的图表数据之间的关系，定义了上升模式、下降模式以及平盘模式，其中定义：

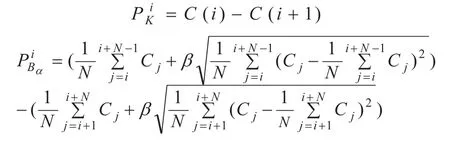
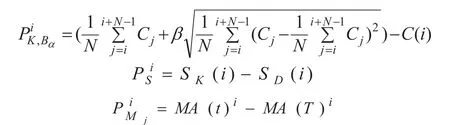
1.1 金融市场数据模式

金融市场中某一时刻的收盘价在布林带指标的上轨线、中轨线或者下轨线附近均可能出现上升模式，以在中轨线附近的上升模式为例，当满足：

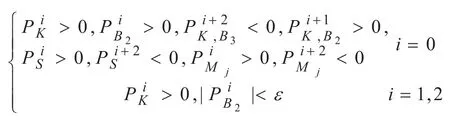
时，即收盘价在布林带指标的中轨线和下轨线之间且呈上升趋势并突破中轨线，此时短期移动平均线由下而上突破长期移动平均线形成黄金交叉，随机振荡指标K线由下而上突破D线发生低位金叉，或者K线和D线均成上升趋势且K线在D线的上方，则预示金融数据将进入上升过程，如图1(a)所示。

同理，当满足条件

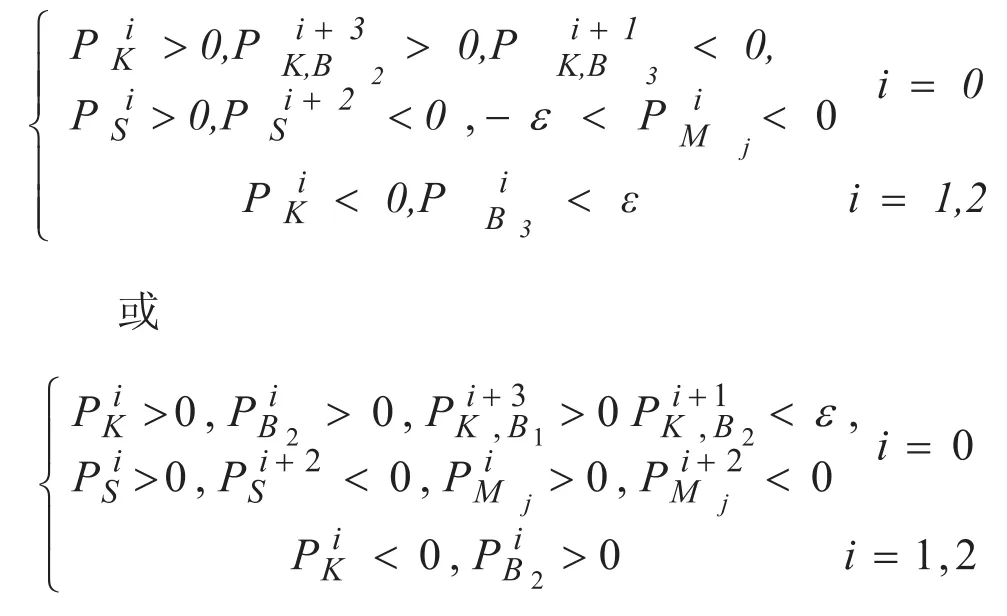
也预示金融数据也将进入上升过程。

同时，在布林带指标的上轨线或者中轨线附近均可能出现下降模式，以在上轨线附近的下降模式为例，当满足：

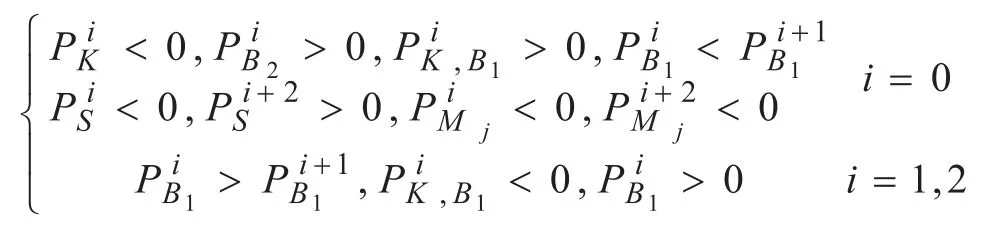
时，即收盘价在布林带上轨线附近由上升趋势变为平缓或下降趋势，且回落到上轨线内部，同时短期移动平均线由上而下跌破长期移动平均线，随机振荡指标发生高位死叉，则预示金融数据将进入下降过程，如图1(b)所示。

同理，当满足条件

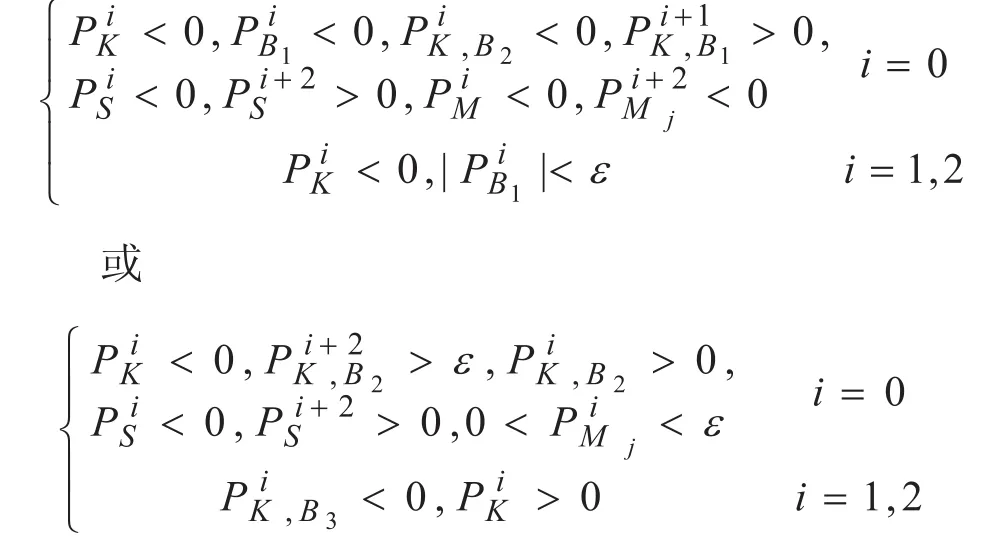
也预示金融数据将进入下降过程。（其中阈值ε=0.0004，δ=40，η=60）

同时，若满足条件

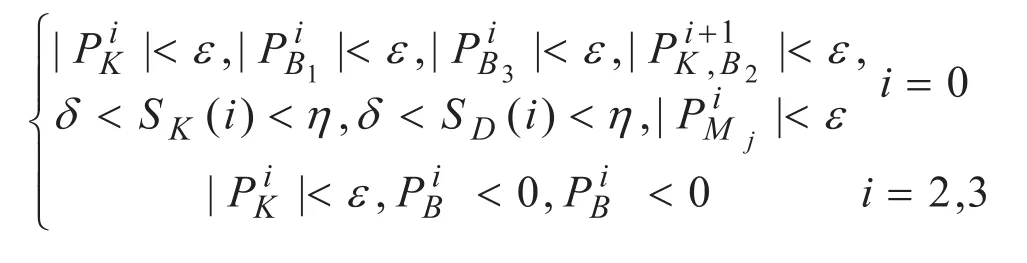
即当前布林带上下轨均呈平缓趋势，且上、下轨之间的通道变窄，收盘价成平缓趋势，同时各移动平均线均处于平缓趋势，随机振荡指标的K线和D线处于40至60的波动之间，则预示金融数据将进入平盘阶段，如图1(c)所示。

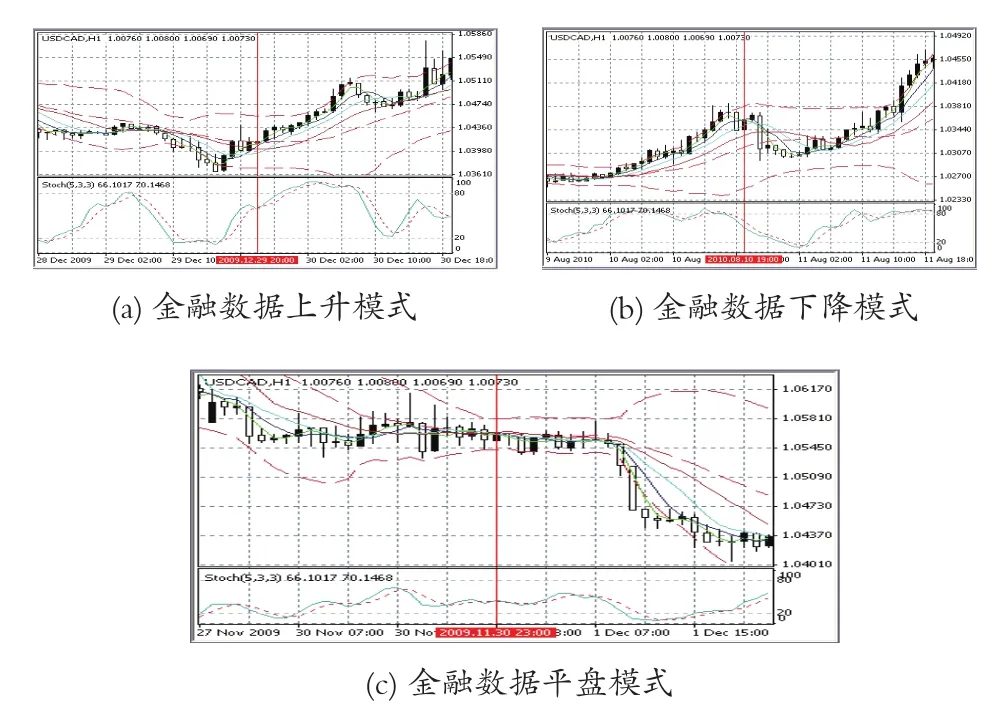
图1 金融市场的数据模式

1.2 金融数据走势判断

如上所述在金融市场中的某一时刻，基于布林带指标、移动平均线指标、随机振荡指标的走势以及与金融市场中的图表数据之间的关系，可以大致判断该时刻的金融数据所属模式，同时，由于金融市场的变化有强弱之分，因此我们需要根据模糊模式识别中的隶属度值来分析金融数据变化的强弱。

2 基于模糊理论的模式识别

2.1 模糊模式识别概述

模式识别的实质就是判定观察对象（元素）和模式类（集合）之间的从属关系。传统的集合论中，元素和集合的关系式非常绝对的，要么属于，要么不属于，两者必居其一，且二者仅居其一。基于传统的集合论的判决方式称为硬判决，其中，待识别的对象只能是属于多类中的某一类。而模糊集合论采用隶属度来描述元素属于一个集合的程度，用来解决信息的不确定性问题。模糊模式识别是以模糊集合论为基础，对应的判决方式是一种软判决，识别结果是观察对象属于某一类的隶属度[3]。

要判断观察对象的隶属度，首先应该确定模式类的隶属函数，而确定隶属函数的方法有很多种，包括：模糊统计法，模糊分布，二元对比排序法，逻辑推理法，专家评判法以及隶属函数逼近法等[4]。

2.2 模式隶属度函数的确定

根据上节所述，本文利用隶属函数逼近法来确定隶属函数，即将所研究的对象用常见的隶属函数作近似，本文选取隶属函数

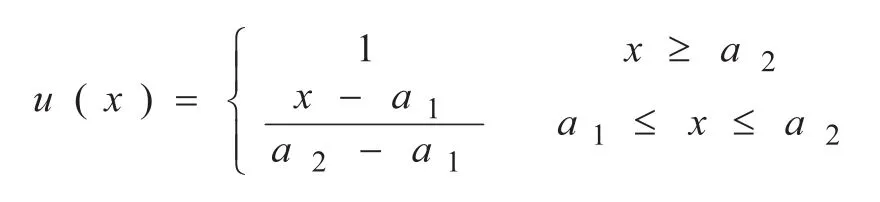
作近似[5]，将指标协同方法构造出的7种模型对应于三个模糊集合，分别为上升模糊集合，平盘模糊集合，下降模糊集合,同时根据金融数据与各指标走势的曲线斜率定义各模糊集对应的隶属度函数。

图2所示为提取的外汇市场中一段时间内的收盘价走势曲线，由图中可以看出曲线是由n段斜率不同的直线组成，所以在求各曲线的斜率 时，首先需要根据曲线各点像素的坐标值求出各段直线的斜率，然后按照各段直线的横轴长度占该曲线总长度的比例得出曲线的斜率。

图2 金融市场中的收盘价走势曲线

如图2中若求a、b点之间的曲线斜率，需分别求出bc、cd、de、ea 4段直线的斜率k1、k2,、k3,、k4,同时定义Xab表示曲线ab的横轴长度，同理 Xbc、Xcd、Xde、Xea分别表示直线 bc、cd、de、ea的横轴长度，则曲线ab的斜率kab为：

同时，根据对历史数据的分析，我们定义当金融市场中收盘价曲线及布林带指标走势与水平线夹角处于-10度至10度之间时，金融数据走势处于平盘趋势；当金融市场中收盘价及布林带指标走势与水平线夹角处于10度至90度之间时，金融数据走势处于上升趋势；当金融市场中收盘价及布林带指标走势与水平线夹角处于-10度至-90度之间时，金融数据走势处于下降趋势。即定义θ表示各曲线与水平线的夹角，则有

因此，根据金融市场中收盘价及各指标走势曲线的斜率可得出各种趋势下模式的隶属度函数为：

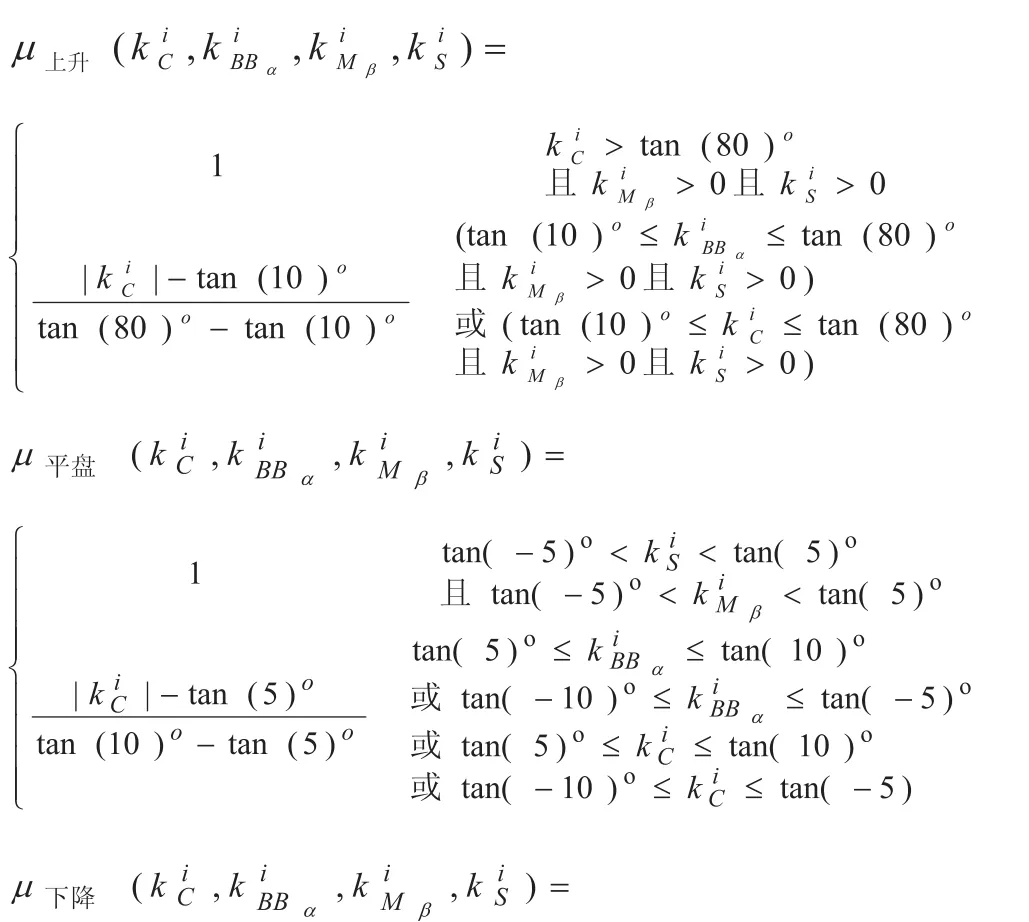
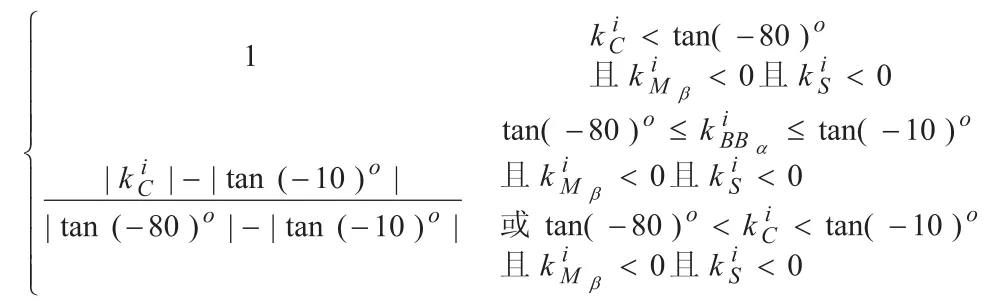
因此，在根据指标协同作用确定金融市场中某一时刻的数据走势所属模式类的同时，可根据各模式类的隶属函数确定该时刻金融数据走势属于此模式类的强度，为定量分析金融数据的走势奠定了基础。

3 实验

本文选取当前最大的金融市场——外汇市场来对上述方法进行验证，首先基于FXDDMetaTrader平台对货币对USDCAD在H1时段下2010年9月17日14:00处的外汇数据进行分析，如图3中的垂直线处，具体步骤如下：

图3 外汇市场中各曲线走势示例

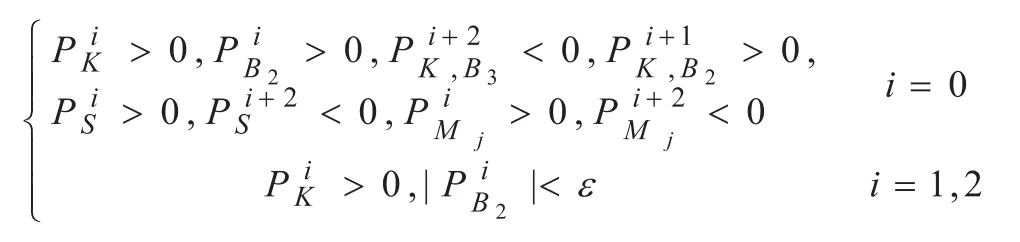
1) 分析图4中各曲线的走势，可得出该时刻各技术指标及汇价满足上升模式，即满足因此可判断该时刻的外汇走势将呈上升趋势。2) 根据各曲线的斜率，分析该时刻汇价呈现上升趋势的强度，首先从图4中提取各曲线，并根据上述方法计算当前时刻与前一反转点时刻之间汇价以及各指标走势曲线的斜率，即图4中点a与点b之间各条曲线的斜率，各曲线斜率值如表1所示。

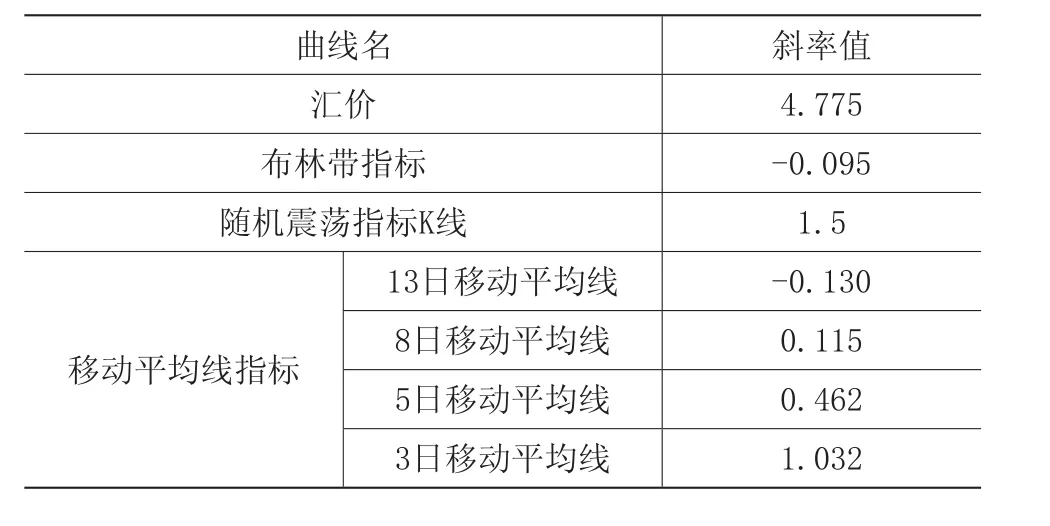
表1 各曲线斜率值

3)根据上升模式的隶属函数得：

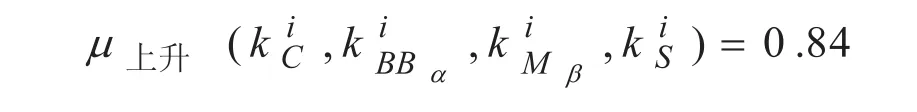
因此可以得出：在H1时段下2010年9月17日14:00时，外汇市场处于上升模式，且上升趋势的强度较大。

4 结论

本文通过综合分析布林带指标、移动平均线指标和随机振荡指标的协同作用，确定了金融市场上升、下降以及平盘过程中的各种模式，同时基于模糊模式识别的隶属度值，得到不同时刻金融数据对于模式类的隶属度，从而确定金融市场中某一时刻数据走势隶属于某一模式的强度，进行了金融市场走势的定量分析的探索，改变了当前金融市场中仅利用模式进行数据分析的现状。

[1] 游宗君,李华东.中国外汇市场的分形结构测度[J].贵州财经学院学报,2008,3 (4):59-64.

[2] 孟力,刘玥,赵晶.基于分形理论下的外汇市场的预测[J].沈阳工业大学学报:社会科学版,2008,1(2):135-139.

[3] 李弼程,邵美珍,黄洁.模式识别原理与应用[M].西安:西安电子科技大学出版社,2008:1-5.

[4] 齐敏,李大健,郝重阳.模式识别导论[M].北京:清华大学出版社,2009:204-209.

[5] 舒宁,马洪超,孙和利.模式识别的理论与方法[M].武汉:武汉大学出版社,2004:107-114.