基于Pareto的制造资源能力评价

潘伟杰，谢庆生，李少波

（贵州大学 教育部现代制造技术重点实验室，贵阳 550003）

0 引言

现有的网络化制造[1]、应用系统服务提供商[2]、制造网格[3]等模式的制造资源能力评估，国内外学者已经进行了大量的研究工作[4-8]。一类是研究基于用户提交的评价信息进行评估，以模糊理论为基础，采用参照物比较判断法来确定指标权重；制造资源评估的方法主要有层次分析法、人工神经网络法、专家评分法、遗传算法、层次分析法和灰色关联理论相结合的制造资源选择策略等；另一类是针对分布在不同地域的制造资源评价和选择问题，建立制造资源评价指标体系，采用熵值法和层析分析法为代表的主客观赋权法分别进行了评价，最后利用组合模型进行综合评价。

本文通过调查研究制造企业高级管理者、高级工程师、专家等人员的意见，分析影响企业制造资源能力的因素，基于Pareto最优性原理，构建了制造资源服务评价指标体系与数学模型，并证明模型的正确性与最优解的存在性。

1 制造资源能力评价指标体系构建

制造资源初步设想可从时间、质量、成本、技术、服务、领先性、企业业绩和社会环境效益等几个方面来进行分析。本文统计出了一个制造资源评价指标，其中整体制造资源能力A。

1）企业核心能力B1

包括企业响应时间（C1）、企业制造成本（C2）、企业技术创新性（C3）、产品质量（C4）以及企业后期服务（C5），针对不同的C1、C2、C3、C4、C5相对应的制约指标包括企业设备生产计划能力，企业生产效率，批量、个性化、及时交货（D3），企业设备状况（D4）；风险最小化（D8），总成本预算 （D7），投标标价 （D6），加工成功率（D5）；企业专利数量（D13），实施协同设计能力（D12），科研投入（D11），设备先进度（D10），工艺、 精度（D9）；合同履行率（D16），企业资产（D15），企业信誉、质量保证体系（D14）；订单任务反馈（D21），服务人员技术（D19），服务态度（D20），制造任务反馈（D18），服务网点（D17）。

2）决策人评价B2

包括决策人个人偏好（D24），群体决策人权威度（D23），单一决策人权威度（D22）。

3）第三方评价B3

包括第三方企业仓库（D27）存储能力，运输能力（D26）以及资金提供商（D25）企业、银行或是个人的不同状况。

4）社会、环境效益评价B4

包括制造业就业岗位（D30），资源消耗指数（D29），制造业废水、废气排放量（D28）等。

2 制造资源能力综合评价数学模型

针对制造资源能力评价指标体系，不同企业指标存在很大的差异，因此，该问题属于多目标最优化问题的范畴。而多标优化问题在科学和工程领域中广泛存在，传统的方法构造单目标评价函数需要决策者事先提供深奥的偏好知识，在某些情况下无法提供偏好信息，大多数单目标优化技术均是基于局部优化的搜索算法，虽然能够找到单目标优化问题的局部或全局最优解，由于不同制造企业制造资源各不相同，而且指标体系构建方法也不尽相同，难以搜索到全部或多个均匀分布的最优解。

假定决策变量x Rm，目标向量Di⊂Rn，i＝1，2，…，30；m表示制造企业数量；Rn为n维向量集。针对本文云制造制造资源能力评价指标体系模型，其多目标优化模型可以描述如下：

对任意的决策向量x1，x2，当且仅当f（x1）＞f（x2），称 x1支配 x2，记为 x1≻ x2；当且仅当 f（x1）≥f（x2），称x1弱支配x2，记为x1≻＝x2；当且仅当 ¬ f（x1） ≥ f（x2）?¬ f（x2）≥ f（x1），称 x1与x2无关，记为x1x2。对任意的x，如果存在x'，使得 fi（x）≤ fi（x'），（i＝ 1，2，…，m）。其中，至少有一个不等式严格成立，则称x为Pareto最优解，又称为Pareto非支配解、非劣解或有效解[12]。一个多目标优化问题，存在一组Pareto最优解，全部Pareto最优解称为Pareto最优解集，相应的目标向量构成Pareto最优面（多维目标空间的超平面），即Pareto前沿。

3 基于Pareto的制造资源能力评价分析

对于制造资源能力评价的多目标优化问题，它的Pareto最优解（非劣解）和Pareto前沿基本上是确定的，而求解多目标优化问题的目的是把求出Pareto最优集提供给制造企业，制造企业再根据自身的需求以及各方面的综合考虑确定一个最终满足自身的解。本文采用Pareto最优的思想，对制造资源进行分层求解，主要思想如下表示：

1）通过对子准侧指标层中的企业响应时间（C1）、企业制造成本（C2）、企业技术创新性（C3）、产品质量（C4）以及企业后期服务（C5）各个决策向量依据公式（2）分别进行求解Pareto最优解，获得C1、C2、C3、C4、C5的最优解集；

2）对于决策人评价B2、第三方评价B3、社会、环境效益评价B4，依据公式（5）求解对应的Pareto最优解集；

3）对于获得的 C1、C2、C3、C4、C5的最优解集，相对于企业核心能力B1他们都是决策向量，然后依据公式（3）求解目标函数B1的Pareto最优解集；最后根据公式（4）求的总目标层A的最优解集；

4）对于目标函数和决策向量角色的转变，根据不同制造企业的偏好和要求分别建立相对的Pareto前沿，然后将最终的最优解集提供给不同的制造企业，制造企业有针对性的选择自己要求的企业进行建立关系。

以企业响应时间C1、社会、环境效益评价B4和总目标层云制造制造资源能力A为例来求解Pareto最优解说明问题。

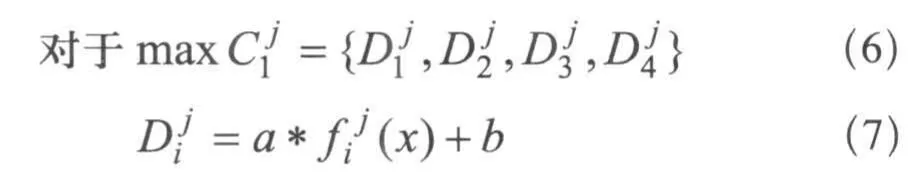
其中，j表示候选制造企业数量，j为非负整数，a, b为自然数。同样道理可以获得Cij的Pareto最优解集。

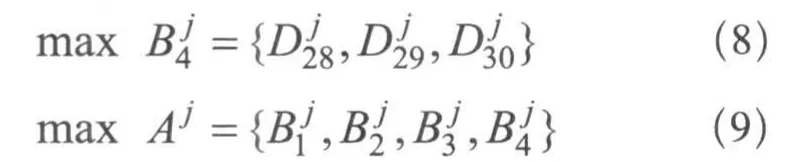
依据公式（2）、（3）、（6）、（7）、（8）、（9）可以得到对于A的Pareto最优解。

同样道理，对于满足Al{DD，D，D，对于k i，满足DD可以求得A的Pareto最优集，制造企业根据最终求得的Pareto前沿，对于最小化问题，Pareto最优性方法基本类似。 如对于境指标是越小越好，故对环境资源指标进行处理，转为求最小化。

为了进一步提高制造企业对制造资源鉴别能力，对求得的Pareto前沿求“不动点”求解。

1）标准化指标向量D＝ (D1，D2， ，D30)。对于一般均衡问题：在指标向量集合D中是否存在一个元素即一个指标向量D*＝(D，D；

2）将指标向量D＝(D1，D2， ，D集合变换成一个有界集合，用各个指标向量之和ΣDi（i＝1，2，…，30）去除该指标向量，使得D中每一个元素D的每一个分量约束在某个有界范围之内，原来的指标向量变换成为新的指标向量D′＝， ，)即：

然后，对于满足Pareto前沿的p′，满足公式Aj＝A， ，中的D中的元素已经成为标准化后D′中的元素，对于给定一个D，更具可以求得满足制造企业的30个指标的A对应的30个指标值。

可以得到一个映射关系：

显然这是一个理想的状态，现实中制造企业不可能完全满足另外一个制造企业的所有要求。但是该“不动点”是否存在，如果真的存在这个“不动点”，那么将候选制造企业的指标和该理想指标进行对比很容易指导制造企业进行决策。

用Di表示制造企业现有的指标值，则理想的指标向量 可以用一个函数更加具体的表示出来，即：

式中所有Ki均大于0。上述函数可以定义为：让某i制造企业的指标满足0到Di＋Ki*Ai中的较大者。其解释是如果原有的指标向量值超过不满足需求时，增加或是降低一个适当的值使其满足理想指标向量。

为了消除新的指标向量 不在标准化价格向量集合D′之内，同样也要对新的指标向量进行一次标准化处理，即用Σ （i＝1，2，…，30）除以每个 ，于是得到：

现在将（10）（13）两个映射复合起来得到一个复合映射g ·f，即：g ·f∶D′→D′ ，其具体形式：

这是一个标准化的指标向量集合 D′到其自身的映射关系，通过g ·f映射得到D′中另外一个相同或是不同的指标向量。根据布劳威尔不动点定理[16]，假设g和f均为连续，同时他们经过标准化有界、闭合凸的集合，于是可以得到“不动点”的存在，即存在理想的指标向量。

通过以上理论分析，最种求得 ，非常直观地提供给不同的制造企业进行选择，使各个指标的赋值达到主观与客观的统一，消除传统方法法中制造企业决策者的主观判断、偏好及对问题的理解等因素对评价结果产生的影响，相对客观地对进行评价，使得最终评价结果更加合理和科学。

4 结论

本文在研究了相关理论的基础上，建立了制造资源能力评价指标体系；运用多目标优化与决策的方法，提出了Pareto最优方法，相对于传统评价函数法、交互规划法、分层求解法等方法，该方法更加直观，而且编程简单，为制造企业决策问题提供新的理论和方法，具有重要的理论和实际应用意义。参考文献：

使新的指标向量值满足[0,1]范围内。得到另外一个A到标准化指标向量集合D′ 映射关系：

[1] 罗天龙,孙克豪.虚拟设计与网络化制造研究综述[J].机械制造, 2004, 42(7):31-35.

[2] 谢庆生.我国制造业ASP发展的模式与策略[J].中国制造业信息化, 2003, 32(1):66-70.

[3] I. Foster. The Grid: A New Infrastructure for 21st Century Science[J]. Physics Today, 2002, 55(2):42-47.

[4] 李伯虎,张霖,王时龙等.云制造—面向服务的网络化制造新模式 [J]. 计算机集成制造系统, 2010, 16(1): 1-7.

[5] 孙林岩, 李刚, 江志斌, 等. 21世纪的先进制造模式—服务型制造 [J]. 中国机械工程, 2007, 18(19): 2307-2312.

[6] 张鹏飞,顾寄南,吕晓凤, 张庆峰. 基于用户评价信息的制造资源综合评价方法的研究[J],机械设计与制造,2010,(7):258-260.

[7] 付景枝,刘婷婷,张友良.制造网格中资源的层次检索方法研究[J]. 计算机集成制造系统,2008,14(5):1008-1014.

[8] 冯蔚东,陈剑,赵纯均.基于遗传算法的动态联盟伙伴选择过程及优化模型[J].清华大学学报(自然科学版),2000,40(10):120-124.