采用交叉耦合补偿的异步电动机矢量控制系统研究

田 清

（重庆水电职业学院，重庆 402160 ）

1 矢量控制的基本方程式

按转子磁场方向的矢量控制的三相异步电动机的电压磁链方程式为

2 考虑铁耗时的定子T轴电流的方程式

在计入铁耗后异步电机定子电流的T轴分量包括两部分：itT控制电机的电磁转矩，而itFe通过等效电阻RFe产生铁耗。

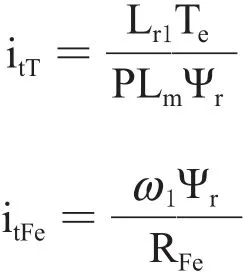
由于在本文所提出的矢量控制方案中电机的速度估算和定子电压解耦都利用了定子T轴电流给定值与实际值的误差项，电机实际的定子T轴电流本身就包含了铁耗所对应的电流itFe，因此在控制器中给定的定子T轴电流也应考虑铁耗对应的电流这样既可以提高速度估算的精度，也可以改善定子电压解耦的效果，提高系统的转矩控制性能。

3 速度估计方法

由感应电动机的运动方程式

当Ψr保持恒定时，可知Te完全由it1决定，因而给定矩电流分量与其实际响应it1之间的差值就反应了转矩的变化特性，对（-）信号经过适当的处理就可得到转速信息。本文采用PI自适应法进行速度估算。PI自适应法的结构如图1所示。

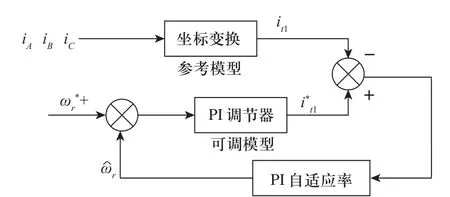
图1 PI自适应法速度估算

由图1可知，这种速度估计方法实际是模型参考自适应法（MRAS）的一个变形，它充分利用了控制系统已有的结构，在此基础上以PI调节器估计转速，且结构比MRAS简单，性能仍比较好。

PI自适应法估算转速的基本关系式为

式中Kp，K1为PI调节器的参数。其中it1由定子电流经坐标变换计算得到，这样可以避免转子参数对其的影响。

图2 定子电压解耦单元

4 交、直轴直流误差项进行电压补偿的动态解耦

在构成异步电机定子交、直轴电压中，除了电机的阻抗压降和反电势外，还有交叉耦合电压ω1σLsim1(it1)，并且此交叉耦合电压和电机的转速有关，在电机的高速运行段有较大幅度的增加。因此，如何消除交叉耦合电压对异步电机定子交、直轴电压计算值的影响是实现交流电机交、直轴电流仅受自身电压控制的关键。

反馈解耦是将感应电机的定子交、直轴电流反馈量直接用于电机交叉耦合电压项的解耦电压计算，并将其引入电机控制电压端进行迭加补偿，以实现感应电机交、直轴电压的解耦。反馈解耦是动态解耦，理论上能对交叉耦合电压项实时完全解耦。但由于电机参数在电机运行中的变化，且电机交叉耦合电压项在电机高速运行段有较大增加，使系统易出现不稳定。

前馈解耦是将控制电机的定子交、直轴电流给定值用于电机交叉耦合电压项的解耦电压计算，再将其迭加到电机控制电压端进行补偿。前馈解耦是稳态解耦控制，采用的是电流给定值而非实际电流，结构较前馈解耦控制简单，但其采用控制器的电机参数，使系统受电机参数实际值影响较大。

为克服以上两种解耦方法的不足，本文提出了一种利用交、直轴直流误差项进行电压补偿的动态解耦方法，以提高系统对电动机电阻参数变化的鲁棒性和控制精度。具有电流误差补偿的定子电压解耦单元结构如图2所示。

由上式及图2可知，T轴电流未达到设定值时，可通过调节器由Rs产生的T轴电压和ω1σLs产生的M轴电压来调节。因此i*t1与定子电流的T轴分量的实际值it1的 误差信号送PI调节器，调节器的输出u’

t1为定子电流T轴分量的误差引起的定子定子电压T轴分量调节量，同时还应在M轴电压分量重增加（ω1σLs/Rs）的M轴电压调节量。由于感应电机参数的特点，ω1σLs＞Rs, (ω1σLs/Rs)＞由此可知，调节定子电流的T轴分量，主要还是由M轴电压的变化来实现。同理，i*m1与定子电流的M轴分量的实际值im1的误差信号送PI调节器，调节器的输出u’m1为定子电流M轴分量的误差引起的定子电压M轴分量的调节量，同时还应在T轴电压分量中增加（ω1σLs/Rs）u’m1的T 轴电压调节量。（ω1σLs/Rs）u’m1＞，因此调节定子电流的M轴分量，主要是由T轴电压的变化来实现。

该图所示的定子电压解耦控制单元的数学模型为

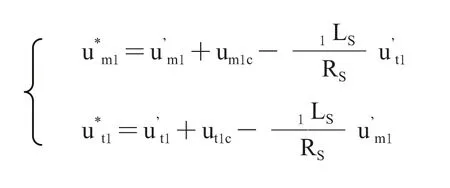
式中，um1c、ut1c是由定子M、T轴给定电流以及定转子磁链构成的定子电压的M轴和T轴分量，它们的表达式如下：

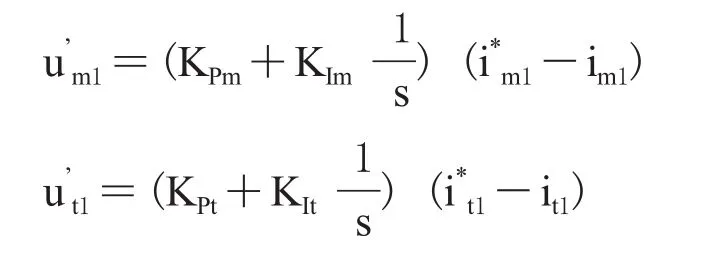
由上述可知，该解耦方法是动态解耦，由于在解耦基础上增设M、T轴电流的给定值与实际值的误差进行PI调节，可以消除定子电阻受温度变化对定子电压的影响：同时，对M、T轴交叉耦合电压项的补偿采用了M、T轴电流误差的PI调节器的输出，且计算的解耦电压比实际的交叉解耦电压值要大，当解耦电压迭加到电机的控制电压端时，加快了电机控制的响应速度，提高了电机在告诉运行段的解耦效果，增强了系统的稳定性。

[1] 陈世坤. 电机设计(第二版)[M]. 机械工业出版社, 1997.

[2] 童春辉. 牵引电机[M]. 中国铁道出版社, 1983.

[3] 陈伯时,等. 交流调速系统[M]. 机械工业出版社, 2002.