高师数学专业开设《几何画板》课的必要性研究

王奋平

(琼州学院理工学院，海南三亚572022)

《几何画板》作为一种具有学习容易，操作简单，功能强大的的教育软件，是由美国Key Curriculum Press公司制作并出版的优秀教育软件，1996年该公司授权人民教育出版社在中国发行该软件的中文版。也是全国中小学计算机教育研究中心在CAI(Computer Assistant Instruction)中推广使用的软件之一，可用在平面几何、平面解析几何、射影几何、代数与函数、向量、微积分等数学内容的学习和教学中，可以方便、快捷地开发出具有实用性的课件;不仅如此，它简单易学，易被掌握，花费较短时间就可以独立制作数学课件，应用于课堂教学，方便快捷，受到广大中小学数学教师的普遍欢迎.

1 几何画板在中学数学教学中的作用

1.1 使得抽象数学形象化，有利于提高教学效率利用《几何画板》的动态功能可以清楚地展示函数图形、几何图形中无法用模具、板书图形描述的性质，例如:“旋转体”之一的圆柱体教学中课本叙述:“圆柱可以看成是矩形以它的一边所在直线为轴，其余各边旋转一周而成的面所围成的几何体。”这一抽象的叙述使学生感到困惑，难以理解，因为看不见又摸不着。而教师利用静止的几何图形又进不清楚。《几何画板》给圆柱体的概念教学提供了现代化的手段。用“跟踪”、“移动”等功能，动态地显示了圆柱展开成为一个矩形的过程，直观地展示了所围成的曲面。同时可看到矩形的另两边通过旋转所形成的平面圆。此过程可分开演示，最后合成演示。这样动画演示使得以往讲不清的概念现在讲清了，抽象的知识形象化了，静态的知识动态化了。减少了课堂上的抽象费时的讲解，为学生观察现象，发现结论，探讨问题创设了较好的“情景”不仅使学生便于理解，而且给学生提供了一个轻松愉快的氛围。用“移动”命令可以实现三棱柱分解为三个三棱锥的形象动画过程，使得相对复杂的图像变换过程简单易懂。

1.2 有利于开展探究性教学《几何画板》的图形对应点的可移动性可以展示代数、几何性质。例如:在复平面内作出两个复数的和的平行四边形图形，然后拖动实部或虚部的对应点，相应的两个复数也发生了变化，可以看到两个复数对应的位置向量也随之变换位置，但无论如何变换实部、虚部位置，四边形两组对边仍然保持平行，学生由此可体会到平行四边形法则的本质。运用几何画板可以准确有效地验证代数、几何的很多定理、性质等，例如:可以严整三角形的内心、外心、垂心、旁心等几何点，还可以验证三角形内角和定理、勾股定理、圆幂定理、相交弦定理、圆周角定理、正弦定理、余弦定理、三垂线定理等，通过鼓励学生自己操作也可以完成上述任务;也可以几何画板为工具进行数学问题的深入研究。例如:在不等式组形成的线性规划问题中，可以移动直线在可行域中探求最值，找到最佳值。还可以在抛物线的绘制过程中通过改变系数，如在讲函数y=Asin(ωx+φ)的图象时，传统教学只能将A、ω、φ代入有限个值，观察各种情况时的函数图象之间的关系，而利用《几何画板》则可以以三条线段的长度或坐标分别代表A、ω、φ的值，作出y=Asin(ωx+φ)图后，当拖动上述三条线段的某一端点时分别改变三角函数的振幅、周期和相位，这样在教学时既快速灵活，又不失一般性。还可以在同一个坐标系中作出多个函数的图象，如在同一个直角坐标系中作出函数y=x2、y=x3和y=x1/2的图象，比较各图象的形状和位置，归纳幂函数的性质。用《几何画板》还可以探究图形性质的不变性:当几个不同对象在某些方面(如特征、属性、关系等)有类同之处，可引导学生合理地联想其他方面也有类同之处，利用变式探索、挖掘、概括、引申获得问题的一般性结果，使特殊问题一般化，零散知识规律化.借助《几何画板》，可以帮助学生发现数学性质和规律，体验“观察—归纳—猜想—验证”的数学过程.

1.3 有利于学生进行自主研究性学习《几何画板》也是一个动态讨论问题的工具，对发展学生的思维能力、开发智力、促进素质教育有着不可忽视的作用，因为几何画板的简单易学，学生可以在教师的指导下很快掌握它的基本功能，经过短暂训练就可以运用《几何画板》进行数学学习，不再有老师滔滔不绝地讲，代之以学生动手“做数学”，老师负责学习的组织，指导学生研究问题，帮助学生学习，成为学生学习的帮助者，学生成为学习的主人。师生可以用《几何画板》为工具共同探讨数学问题，探求未知的结论，可以开阔思路，培养能力，提高数学素养。例如:在学习指数函数与对数函数的概念后，有学生问到当a＞1时，指数函数y=ax与对数函数的图像是否会相交的问题，因为从课本及其它很多参考书上所给的在同一坐标系内指数函数y=ax与对数函数的图像看，当a＞1时，似乎是不相交的，正确的结论究竟是怎样?如果让学生利用《几何画板》在同一坐标系作出函数y=ax和的图像，底数a是可以变化的。当0＜a＜1时，学生通过图像很容易观察出函数y=ax与的图像有且只有一个公共点;当a＞1时，结论是怎样的呢?当a＞1时，通过拖动线段AB上的点a可以发现当a＞1.45时，两函数图像没有交点，当1＜a＜1.45时，两函数图像有两个交直观、形象的动态几何环境，通过学生们自己动手操作，得到最终的结果后，同学们都十分兴奋，取得了良好的教学效果。

1.4 有利于培养学生创造性思维思维的创造性是指完成思维活动的内容、途径和方法的自主程度，并通过独立思考创造出有一定新颖的成分，寻求变异，勇于创新。它常以广泛的联想，引申及转换等思维方法为基础。而有关轨迹的教学是几何中一个重要知识点，且又是一个难点。难就难在需用运动的观点来看几何图形。过去教师借助于静态的图形或教具，试图通过生动的讲解引导学生进入情景，从而在学生头脑中产生画面。但结果只有少数感性知识丰富的学生才能做到。要达到上述目标并非容易，但《几何画板》的动画功能和轨迹功能，可以直观地演示出轨迹生成的过程，不仅使分析、过程、结果一目了然，而且还由此发现许多新的规律。可以帮助我们达到培养学生创造性思维目的，例如在运用几何画板绘制椭圆图形时，学生往往会由椭圆的绘制方法联想到双曲线、抛物线的绘制方法，同时还可以想象出圆锥曲线的统一图形绘制方法，通过一个方程(可以是普通方程也可以是极坐标方程)变换出三种不同的圆锥曲线图象。笔者指导一个学生学习椭圆画法后，该学生就很快总结出椭圆的6种不同画法，同时在画椭圆后又利用“跟踪点”命令想象出几个旋转体的画法，令人赞叹，达到所谓“师不必贤于弟子”的效果，也增强了学生的自信心以及老师自身的教育成功感。教师也颇有“教无止境”之感，激励教师不断进取。

1.5 增强学生学习数学的兴趣因为几何画板的即时、快捷作图功能以及动画、彩色、变换等功能，也可以和用Flash或Authware制作的动画图形结合使用，增强了动感效果。《几何画板》还可以用于分形几何作图，在高中数学课程标准的数学文化中提到几何分形，运用《几何画板》可以作出平面几何中三角形的n极分形、盒子分形、分形树等。不仅让学生接触到了一个全新的数学发展领域，还让学生了解和体会到递归思想和迭代方法的重要性，而且又可以深刻形象地理解数学思想方法，整个过程中可以培养学生的探索能力和创新思维，体验到新的研究方法，发展其辩证思维和提高其审美情趣，增强对数学的学习兴趣。

1.6 有利于提高解题效率《几何画板》不仅能够动态地展现出几何对象的位置关系、运行变化规律，是数学教师制作课件的有利工具，有较强的作图功能，还可以借助于《几何画板》做出图象，观察图象的动态变化，进而把“数”的问题转化为“形”的问题，把抽象的问题转化为直观的问题，对解函数类代数题题有很大的帮助。要想研究函数性质，最直接的方法就是利用函数的图象，我们在分析这类问题时，利用《几何画板》绘制函数图形，提高了学生对图的重视程度，特别是让学生学会利用性质作图、利用图象来分析函数性质，培养了学生的数形结合思想象来分析函数性质，培养了学生的数形结合思想。

例1 (2008年四川高考题)已知函数f(x)=16ln(1+x)+x2－10x，若直线y=b与函数y=f(x)的图象有3个交点，求b的取值范围。

解:

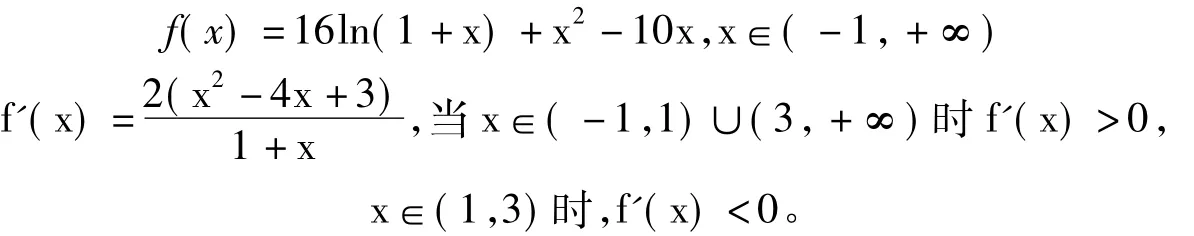
所以f(x)的单调增区间是(－1，1)，(3，+∞)，所以f(x)的单调减区间是(1，3)。

所以f(x)的极大值是f(1)=16ln2－9，极小值是f(3)=32ln2－21。

因此可得

所以在f(x)的三个单调区间(－1，1)，(3，+ ∞)，(1，3)上，直线 y=b与y=f(x)各有一个交点，当且仅当f(3)＜b＜f(1)，b的取值范围是(ln2－21，16ln2 －9)。

图1

1.7 和其他信息技术工具相互配合，优化授课效果如果数学老师能够在中小学数学教学中把相关的软件进行有机组合搭配，会达到事半功倍的效果，大大提高数学课堂教学效率，例如:在解析几何教学中如果能够运用MATLAB或Mathmatics软件用于作图，可以形象显示出马鞍面、玫瑰曲线、心脏形曲线以及其他各种相对复杂而且用《几何画板》难以画出的复杂函数曲线，用《几何画板》绘制的图形可以轻松复制到幻灯片(PPT)中，也可以用超链接方式和幻灯片衔接使用，设计整体性数学教学课件。

2 高师数学专业学生及在职数学教师对几何画板的掌握情况

笔者在担任数学课的琼州学院数学系2004级、2005级、2006级专科班，2003级、2004级、2005级、2006级本科班400多学生的调查中得知:对几何画板熟练掌握的人几乎没有，基本掌握的有4人，基本都是在中学阶段看到有老师使用而感兴趣自学的，绝大多数同学对几何画板一头雾水。对海南省参加省级在职初中数学教师教师培训班的来自全省各县22名学员的调查结果显示:只有一名教师能够运用几何画板作简单初中几何点、线、圆、矩形等基本的图形，其他命令基本不会使用，其余老师完全不会使用几何画板，访谈后了解到，这些学员中有两个教师在自己工作的学校曾经见到有同事使用几何画板辅助教学。大多数学员听说过这个工具，但是因为没有学习机会，一直不会使用。

3 高师数学专业有开设几何画板的必要性

《几何画板》在数学教学中具有传统教学方法无法比拟的巨大优势，只要数学教师能在平常的数学教学中主动、自觉地应用《几何画板》为教学服务，就能更好地培养学生自主学习、探究问题的能力，就能激发和调动学生进行学科学习的积极性，就能把学生从庸俗的电脑游戏中解脱出来，利用电脑为自己的学习服务。《几何画板》作为一个学生自主学习的平台，必将为学生的自主学习、探究学习提供一个广阔的空间，成为培养学生创新思想的实践园地，但是这种优势与在职数学教师和高师数学专业在校大学生对该软件的掌握情况形成鲜明反差，因此，高师数学专业应该将此课程作为必修课程，引导大学生以《几何画板》为工具大胆开发相关数学课件，开展辅助教学授课比赛等各种活动，极力大学生尤其是即将就业成为数学教师的毕业班学生熟练掌握这个对中小学数学教师的教学工作非常有帮助的工具。

［1］陶维林.几何画板实用范例教程［M］.北京:清华大学出版社，2001:46－65.

［2］傅金泉.利用《几何画板》培养学生自主探究学习［J］.网络科技时代，2007(6):23－25.

［3］潘卓.利用《几何画板》制作分形几何图形［J］.中学数学月刊，2008(7):33－35.

［4］周国华.几何画板与解题研究［J］.延边教育学院学报，2009(2):113－116.

［5］徐祖德.用《几何画板》探究图形性质的不变性［J］.中学数学月刊，2009(8)):31－32.