全镀银膜四面锥尖光增强的数值求解

姜宇驰

（常熟理工学院 物理与电子工程学院，江苏 常熟 215500）

光子扫描隧道显微镜突破传统光学显微镜的分辨率极限，是近场光学显微镜的一个典型应用实例.光纤探针是光子扫描隧道显微镜的关键元件，在近场成像过程中，优良的探针能获得较真实的样品形貌图形和较高的接收效率，减少无关的背景光学信息[1].最早的近场光学显微镜中的小孔装置是利用顶端留有小孔的镀金属膜石英小棍或中空玻璃管.在此基础上应用较广的是在单模光纤顶端留有小孔的镀金属膜光纤探针[2]，后来发展的无孔径探针又使得探针尖端附近有了更大的光增强和更高的分辨率.金属的表面等离子体激元共振效应为光纤探针的设计提供了思路，无孔径的光纤探针尖外表镀金属膜，在尖端小孔径处适当残留较薄的金属膜层或者在光纤尖端黏附一个金属纳米粒子同时起到小孔径和增强的作用[3].散射型的无孔径近场光学显微镜采用侧面照射金属镀膜光纤尖不受这个光强极限的影响，所以近年来在实验和理论方面都引起人们越来越多的关注[4].本文利用（FD）2TD[5，6]数值方法对全镀银膜的四面锥尖进行了数值计算，并比较分析了波长分别为355nm和800nm的平面波分别从锥底面和侧面入射在尖端近场范围光增强的情况.

1 (FD)2TD方法

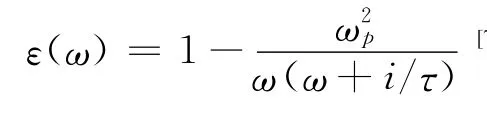
2 计算模型

图1（a）、（b）分别指入射光从锥底面和侧面入射的情况.偏振方向和波矢量如图所示.

锥芯材料为SiO2，锥面角为90°.计算空间的网格数为150×150×100，每个网格大小为3×3×3nm3.

3 计算结果及讨论

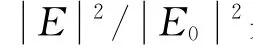
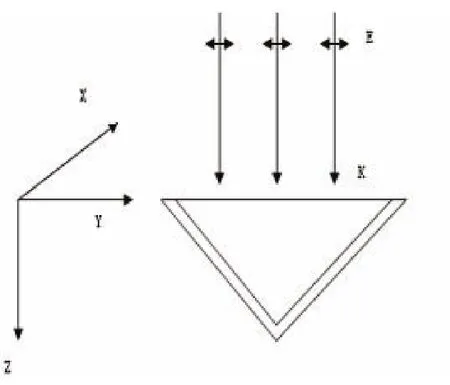
图1 (a)入射光从锥底面入射

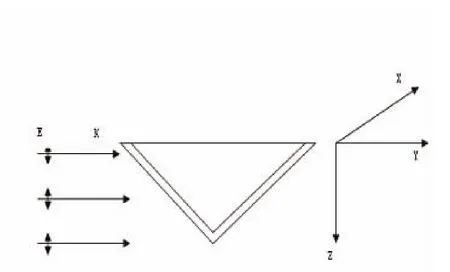
图1 (b)入射光从锥侧面入射

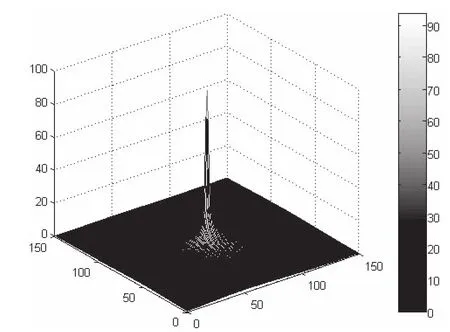
图2 (a）355nm平面波从底面入射时最大光增强

当355nm的平面波从四面锥底面和侧面入射时（如图2所示），锥尖所在平面的最大光增强均在80左右，此外，两者产生的光斑大小均小于10nm.

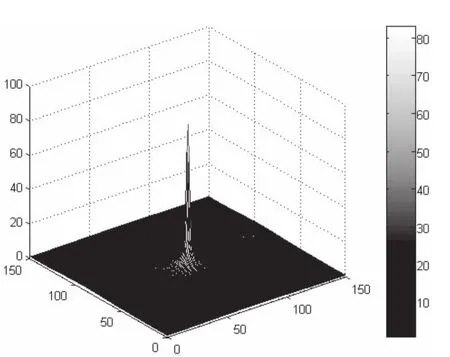
图2 (b）355nm平面波从侧面入射时最大光增强

当800nm的平面波从四面锥底面入射时，锥尖所在平面的最大光增强为3100（图3（a））；当从侧面入射时，锥尖所在平面的最大光增强则为1600（图3（b））.此外，两者产生的光斑大小均小于10nm.

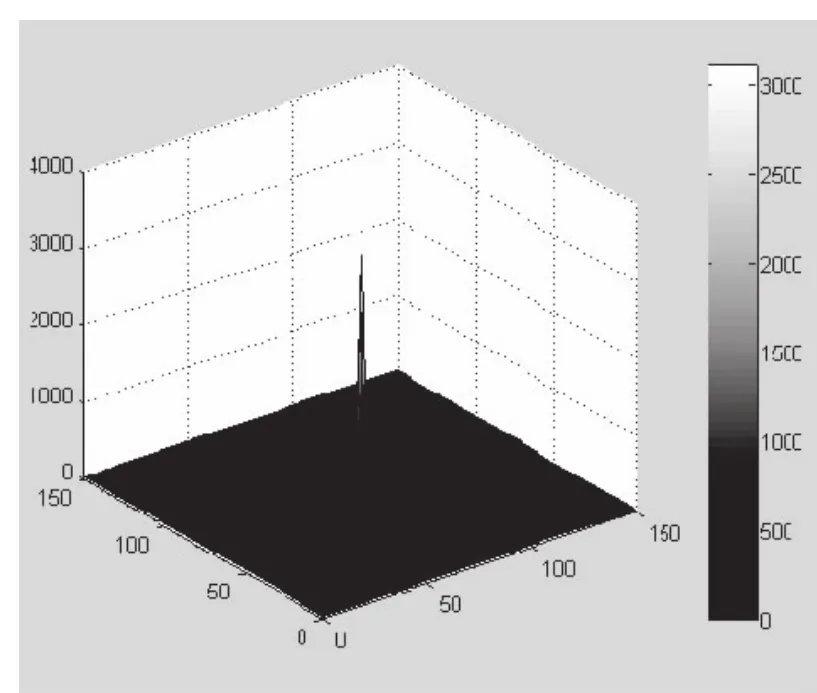
图3 (a）800nm平面波从底面入射时最大光增强

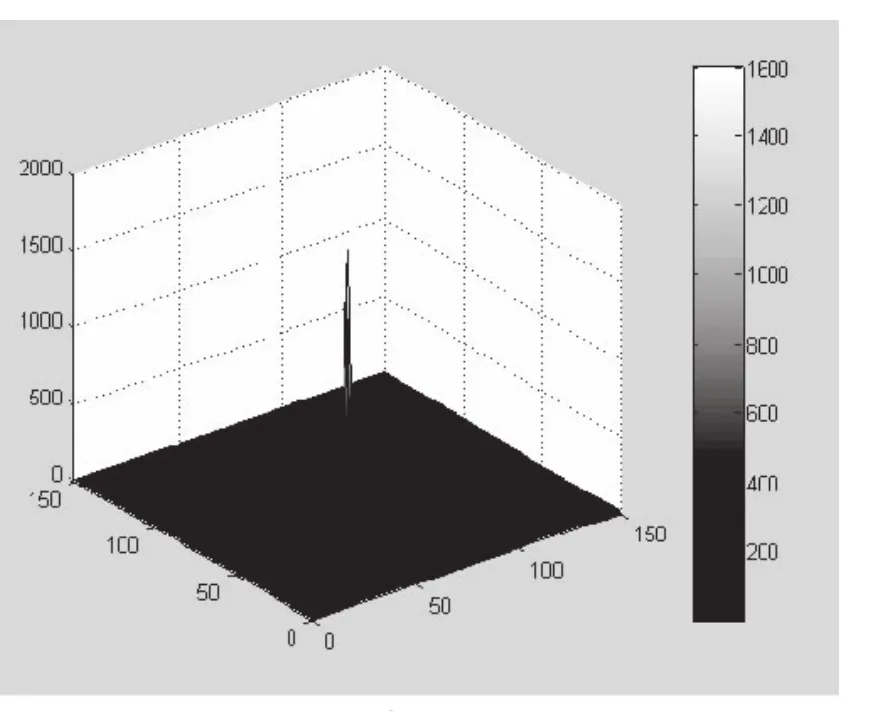
图3 (b）800nm平面波从侧面入射时最大光增强

由结果可知，波长较大的入射光从底面入射时可以在锥尖所在平面获得较大的光增强.由于金属对波长较长的光的吸收作用不是很强，所以从底面入射时，光能大部分转化为表面等离子激元的共振能量，而对表面等离子激元而言，相应波的传播方向趋于结构尺寸减小的趋势[8]，从而能在尖端引起较大的光增强.而入射光波长较小时，无论从四面锥尖的侧面还是底面入射，金属对光的吸收能力加强，大部分光能被金属膜吸收，导致锥尖所在平面处光增强均很小.

本文利用（FD）2TD方法对不同入射光波长分别从底面和侧面照射下全镀银膜四面锥尖端近场的光增强分布进行了数值模拟，结果表明：采用全镀银膜的四面锥尖不仅可以突破传统透镜聚焦光斑受衍射极限的限制，能够获得纳米尺度的聚焦光斑，而且较大波长的入射光从底面入射时能够获得更大的光增强，这在近场光学研究领域有着重要的应用前景.

[1]Wurtz G,Bachelot R,Royer P.A Reflection-mode Apertureless Scanning Near-field Optical Microscopy Developed from a Commercial Scanning Probe Microscopy[J].Review of Scientific Instruments,1998,69:1735.

[2]Veerman J A,Otter A M,Kuipers L,et al.High definition aperture probes for near-field optical microscopy fabricated by focused ion beam milling[J].Appl Phys Lett,1998,72:3115-3117.

[3]Kalkbrenner T,Ramstein M,Mlynek J,et al.A single gold particle as a probe for apertureless scanning near-field optical microscopy[J].Microsc,2001,202:72-76.

[4]Larsen R E,Metiu H.Resolution and polarisation in apertureless near-field optical microscopy[J].Chem Phys,2001,114:6851-6860.

[5]Luebbers R J,Hunsberger F,kunz K S.A frequency dependent finite-difference time-domain formulation for transient propagation in plasma[J].IEEE Trans Ctions on Antennas and Propogation,1991,39:29-34.

[6]Luebbers R J,Hunsberger F,Kunz K,et al.A frenquency-dependent finite-difference time-domain formulation for dispersive materials[J].IEEE Trans tro-magnCompat,1990,32:222-227.

[7]Johnson P B,Christy R W.Optical constant of the nobel metal[J].Phys Rev B,1972,6:4370-4379.

[8]汪国平.表面等离子激元纳米集成光子器件[J].物理学和高新技术，2006，35（6），502-507.