有限长度钝体尾流的三维特性

王汉封

(中南大学 土木与建筑学院，湖南 长沙，410075)

有限长度钝体尾流的三维特性

王汉封

(中南大学 土木与建筑学院，湖南 长沙，410075)

运用X形热线，对高宽比分别为3，5和7的有限长度方形截面柱体尾流进行测量，并运用相平均方法对其尾流场进行研究。相关实验是在一低湍流度风洞中，雷诺数Red为3 500的条件下进行的。研究结果表明：壁面边界层与柱体自由端面后的下降流造成了柱体尾流显著的三维性；该三维性在柱体下游 10d(d为柱体的宽度)处仍能清晰的观察到；对于高宽比为3的柱体，相平均的脉动速度以及脉动速度能谱在所有测量高度上均近似相同；而高宽比为5或7时，尾流中间高度附近流动周期性最强，且相平均脉动速度最大值为柱体顶部或底部附近对应值的2倍以上。

尾流；涡街；热线风速仪；相平均

柱体的绕流和尾流问题普遍存在于工程中，如高层建筑物、水下结构等受到的由流动所诱发的力。针对二维钝体尾流，已开展了大量的研究[1−5]。而工程中所遇到的往往是一端固定于壁面，另一端为自由端的有限长度钝体的尾流。在平面边界层以及钝体自由端的影响下，其尾流与二维钝体尾流有显著区别[6−9]。Kawamura等[10]提出了有限长圆柱体的尾流模型，认为当柱体长径比超过某一临界值时，尾流大部分区域仍由 Kármán涡街控制，而尾流的上半部分则由一对产生于柱体自由端的沿流向的顶部涡所控制；当长径比小于该临界值时，Kármán涡街消失，整个尾流由该顶部涡控制。Sakamoto等[11]研究有限长度钝体尾流的斯坦顿数St与雷诺数Re的关系，发现当长径比为2～3时，St−Re曲线的斜率发生改变，并认为此时在边界层和顶部涡的作用下尾流结构发生了改变。从文献[6−7,11]可知，当钝体为有限长度时，平面边界层与产生于自由端的顶部涡会影响柱体侧面所脱落涡(即 Kármán涡街)的产生，使其明显区别于二维钝体的尾流。当钝体高宽比变化时，边界层与顶部涡的相对作用范围会有所变化，因此，尾流特性也会明显受高宽比的影响[6−7]。为系统比较高宽比对正方形截面有限长度柱体尾流的影响，本文作者运用了X形热线对高宽比为3，5和7的柱体尾流进行测量。运用相平均方法对测量数据进行处理，得到不同高度上时间平均速度、雷诺应力以及相平均雷诺应力等统计参数。

1 实验方法

实验在1个开式低湍流度风洞中进行，该风洞本底湍流度为0.7%，工作段尺寸(长×宽×高)为1.2 m×0.3 m×0.3 m。一正方形截面柱体固定于1个水平平板上，柱体宽度d＝10 mm。实验装置和坐标系的定义如图1所示。实验中，自由来流速度U∞＝6 m/s，对应的基于柱体宽度的雷诺数Red＝3 500。水平板距风洞底面约为0.1 m，平板前边缘经光滑处理以防止流动分离。柱体中心距离水平板前边缘距离为0.33 m。在柱体轴线位置处，水平板上的边界层厚度约为 1 mm。实验中，分别测量了高宽比(H/d)为3，5和7的柱体尾流。X形热线与相应的参考热线布置在柱体轴线下游10d的位置。对每一柱体，分别在不同高度上进行测量。考虑到流场的对称性，实验仅在y≥0的范围内进行。

图1 实验装置及坐标系示意图Fig.1 Experimental setup and coordinate system

为了对测量数据进行相平均，在X热线的另一侧布置了1个单丝热线以提供相位参考信号。参考热线位于x*=10，y*≈4。本文中上标“*”表示用U∞和d进行无量纲化。在所有测量中，参考热线高度与X热线保持一致。参考热线在流动方向上稍为倾斜，如图 1所示，以得到最好的周期性信号。实验中，每个通道的采样频率为3 kHz，每个测量点上的采样时间为20 s。以二维方形柱体的St数可估算本实验中涡团脱落频率约为70 Hz。实验中热线采样频率远高于该值。

图2 柱体中间高度上v的瞬时值与过滤后的值Fig.2 Instantaneous and filtered v signal at mid-span

图2所示为不同高宽比柱体中间高度上，y*=2处速度v以及其过滤后的值。图2所示为各瞬时的相位关系(不同高宽比柱体对应纵坐标比例并不相同)。从图2可以看出：当H/d为5和7时，原始信号与过滤后的信号都具有显著的周期性；当H/d为3时，虽然过滤后信号仍具有周期性，但该周期性在原始信号中已经相对较弱。由于所有过滤后信号均具有周期性，由此可确定任意时刻所对应的相位。以式(1)确定相位参考点：0，π和2π(如图2所示)，式中下标“f ”表示过滤后的值。时间序列上任意其他点的相位可由式(2)确定。通过上述方法可确定所有测量数据的相位，具有某一相同相位的瞬时值可进行相平均，具体方法参见文献[12−13]。通过相平均方法，可以把任何瞬时量进行三元分解[14]，如式(3)所示。

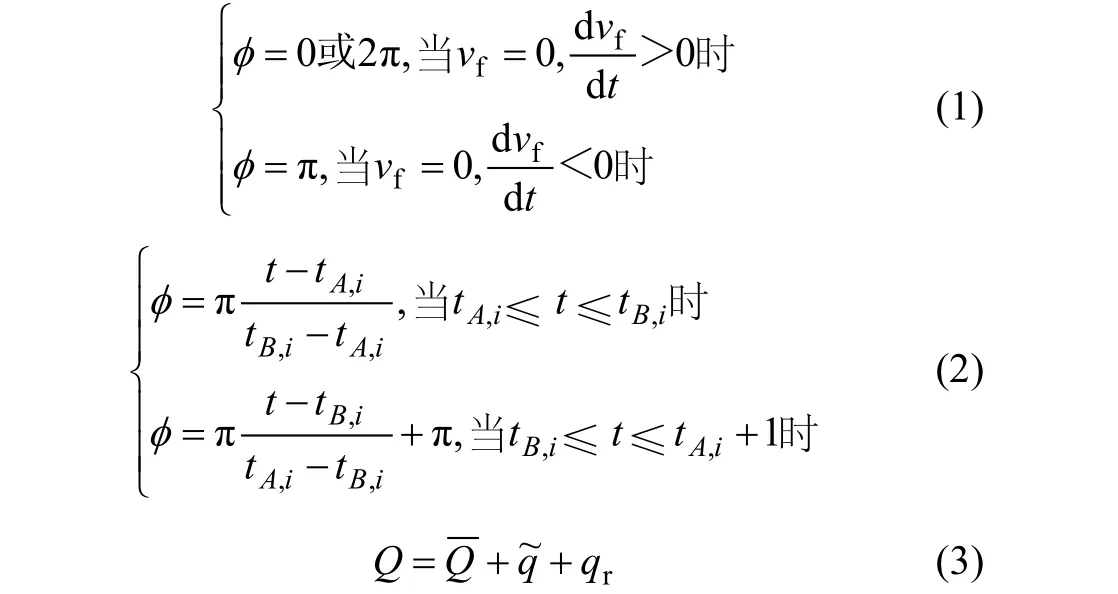
式中：为速度、涡量或雷诺应力等瞬时量；为时间平均值；为周期性拟序结构所带来的脉动部分；qr为非周期性运动带来的随机脉动部分。

2 实验结果与分析

2.1 尾流周期性

图3 尾流中不同高度上速度v的能谱Fig.3 Power spectral density function of v at various z*

图3所示是H/d为3和5时，尾流中不同高度上y*=2处速度v的能谱。H/d=7的能谱与H/d=5时的能谱非常类似，故在此未给出。由图 3(d)～(f)可知：当H/d=5时，不同z*处能谱都有明显的峰值，且其所对应的频率均相同；对应的无量纲频率即St数为0.12，略小于二维方形柱体尾流所对应的值 0.13[2]；对于有限长柱体，自由端后的下降流使钝体两侧所脱落的涡相互远离，使整个尾流变宽，从而降低了涡脱落频率[15]。当H/d≥5时，柱体中间高度附近能谱峰值最强，而靠近两端时峰值减弱。这一现象是由于自由端后的下降流和底部平板边界层的三维性削弱了其附近尾流的周期性。由图 3(a)～(c)可知：当H/d=3时，在所有高度上能谱都是类似的，且没有明显的峰值，这与H/d=5时的情况有着显著的不同。表明当H/d=3时，来自自由端的下降流和底部平板上的边界层已经影响了整个尾流，尾流中的Kármán涡街非常弱。

2.2 相平均脉动速度

如图3所示，H/d=3时尾流中周期性运动已很弱。因此可知由拟序结构所带来的相平均脉动也很弱，故在此未给出。图4所示为H/d=5时不同高度上的相平均脉动速度。与尾流周期性类似，H/d=7时的相平均脉动速度与H/d=5时的对应值定性上是类似的，故在此也没有给出。图4中各图长宽比例是由y方向的测量范围与涡传播速度以及涡脱落频率来确定的[12]。从图 4可知：在所有测量高度上都大于。在中间高度附近由拟序结构所产生的和最大，说明该处尾流的周期性最强，这与图3(b)所反映的信息是一致的。对比图4(a)和(d)与图4(c)和(f)可知：在靠近自由端时，和均弱于靠近底板时的对应值。可知：在x*=10处，自由端后下降流的影响要大于底部边界层的影响。值得注意的是，在z*=5时，的分布出现类似两列涡街的分布，这应该是自由端后下降流所带来的速度较高的流体与由柱体两侧所脱落的准二维的Kármán涡街相互作用的结果[15]。比较H/d分别为3, 5和7的结果可知：当H/d≥5时，柱体中间高度处尾流具有显著的周期性，而靠近两端时相对较弱；而当H/d≤3时，整个尾流场的周期性均较弱。Okajima[2]对不同长径比的圆柱尾流进行了研究，发现当长径比为2～3时，柱体尾流中的涡脱落频率会发生突变。他认为这是由于当长径比小于这一临界值时流场的性质发生了变化，即尾流从准二维的 Kármán涡街结构变成由下降流所控制的对称的尾流结构，周期性也变弱。这与实验观测结果类似。

2.3 时间平均速度及雷诺应力

图4 H/d=5时的相平均脉动速度Fig.4 Phase-average fluctuation velocity for H/d=5

图5所示为不同高宽比柱体尾流中的沿流向的时间平均速度在不同高度上的分布情况。当H/d为3, 5和7时，在= 1的高度上，的分布定性上都是类似的。这说明靠近柱体根部的流动主要被边界层所控制，而与柱体的高宽比没有明显的关系。在距离自由端为1d的高度上，3个高宽比柱体的尾流中均出现类似的分布，即在尾流中心附近(y*≈0)，出现了明显的峰值，如图5所示。这与二维钝体尾流中对应的速度分布有着显著的区别。造成这种自由端附近呈现W形分布的原因是有限长钝体自由端后形成的沿流向的顶部涡会将尾流区域外具有较高速度的流体带入尾流中。这一规律与Wang等[6,9]所给出的有限长柱体尾流模型是吻合的。值得注意的是：在图 5(c)中，的分布在=3和4处几乎完全重合。由此可知：在H/d=7时，柱体中心高度附近的流动已具有一定的二维性。

图6所示为H/d为3和5时，尾流中时间平均的雷诺应力和以及对应的由拟序结构所带来的雷诺应力，即和。如前所述，H/d=5和7时的结果是类似的，故H/d=7的结果在此没有给出。由图6可知：H/d=5时雷诺应力远大于H/d=3的对应结果，可见尾流中的周期性拟序结构有增强雷诺应力的趋势，且对v2更为显著。对于3个高宽比的柱体，在自由端高度上的雷诺应力均小于其他高度上的对应值。这是因为自由端后的下降流会将自由流中的流体引入尾流中，而这部分自由流具有较高的速度(如图5所示)和较低的脉动速度。如图6(a)和(b)所示，在柱体自由端的高度上，的峰值出现在y*≈2附近，这与二维方形柱体尾流的情况完全不同。在二维方柱尾流中，当x*＞4时，的峰值出现在尾流中心。这一现象同样是下降流带入尾流中的低湍流度的流体所造成的。由图 6(a)和(b)可知：拟序结构对时均雷诺应力的贡献非常小，且这一现象对于高宽比较小的柱体更为显著。对于二维钝体尾流，在x*≥40时，拟序结构对雷诺应力的贡献近似为0[12]。而在本实验中，当x*=10时，这一贡献非常小。这说明在有限长度三维钝体尾流中，拟序结构在x*=10处已非常弱。

图5 尾流中时间平均的流向速度的分布Fig.5 Lateral distribution of in wake

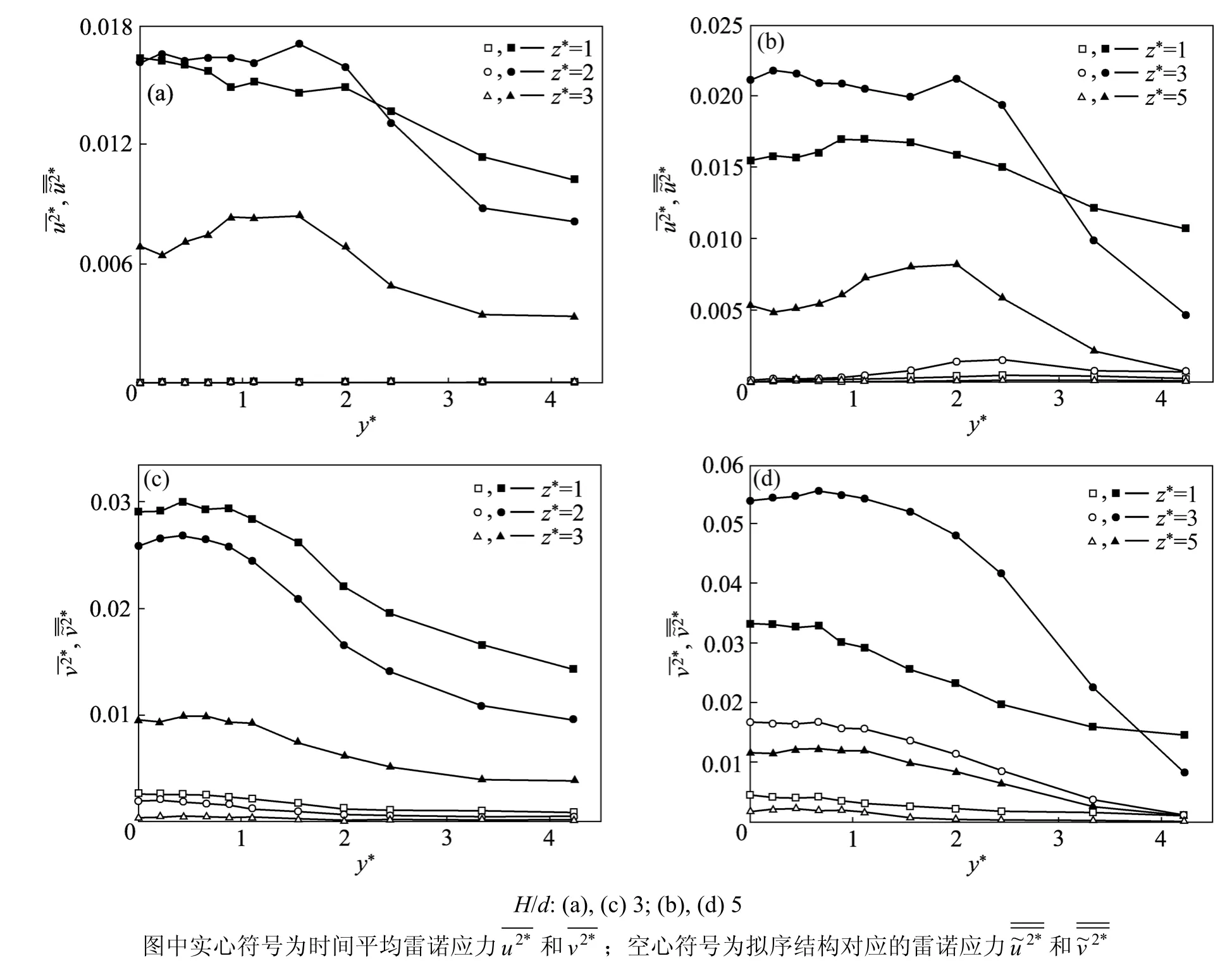
图6 尾流中雷诺应力的分布Fig.6 Distribution of Reynolds stresses in wake

当H/d=5时，在中间高度上和明显大于其他高度上的对应值，这也验证了在此高度上拟序结构是最强的。而当H/d=3时，和在=1时最大。这可能是因为当z*=2时已经受下降流的影响，抑制了和。拟序结构对的贡献远大于其对的贡献，且这一现象随柱体高宽比的增加更为显著。此外，当=1时，和对3个高宽比的柱体尾流都是近似的。也就是说，在这个高度上的流动特性主要由平板边界层所控制，而与柱体高宽比关系不大。

3 结论

(1) 对于有限长度方形截面柱体，当高宽比H/d≥5时，尾流中间高度上的流动具有明显的周期性拟序结构。这一拟序结构随着靠近柱体的两端而逐渐减弱；当H/d=3时，由于自由端后下降流以及底部边界层已影响到整个尾流范围，整个尾流中都未出现明显的拟序结构。

(2) 自由端后的下降流将一部分具有较高速度且较低湍流度的流体引入了尾流中，造成其与二维钝体尾流有显著区别。在靠近自由端的高度上，尾流中心部分速度较高，而雷诺应力较小。这一规律随高宽比的增大而更加明显。

(3) 由于周期性拟序结构较弱，有限长柱体尾流中雷诺应力均小于二维钝体尾流中的对应值。这一规律随高宽比的减小而更加显著。拟序结构对的贡献远大于其对的贡献。尾流中尤其是其中间高度上，拟序结构对雷诺应力的贡献随着高宽比的增大显著增加。

[1]Saha A K, Muralidhar K, Biswas G. Experimental study of flow past a square cylinder at high Reynolds numbers[J]. Experiments in Fluids, 2000, 29(66): 553−563.

[2]Okajima A. Strouhal number of rectangular cylinders[J]. Journal of Fluid Mechanics, 1982, 123: 379−398.

[3]Durao D, Heitor M, Pereira J. Measurements of turbulent and periodic flows around a square cross-section cylinder[J].Experiments in Fluids, 1988, 6(5): 298−304.

[4]Zhou Y, Antonia R A. A study of turbulent vortices in the near wake of a cylinder[J]. Journal of Fluid Mechanics, 1993, 253:643−661.

[5]Zhang N, Li G Z, Huang J C. Numerical study of vortex shedding from a square cylinder and its effects on heat transfer of mixed convection[J]. Journal of Hydrodynamics B, 2003,15(3): 103−111.

[6]Wang H F, Zhou Y, Chan C, et al. Momentum and heat transport in a finite-length cylinder wake[J]. Experiments in Fluids, 2009,46(6): 1173−1185.

[7]Summer D, Heseltine J L, Dansereau O J P. Wake structure of a finite circular cylinder of small aspect ratio[J]. Experiments in Fluids, 2004, 37(5): 720−730.

[8]Adaramola M S, Akinlade O G, Sumner D, et al. Turbulent wake of a finite circular cylinder of small aspect ratio[J]. Journal of Fluids and Structures, 2006, 22(6): 919−928.

[9]Park C W, Lee S J. Free end effects on the near wake flow structure behind a finite circular cylinder[J]. International Journal of Wind Engineering and Industrial Aerodynamics, 2000,88(2): 231−246.

[10]Kawamura T, Hiwada M, Hibino T. Flow around a finite circular cylinder on a flat plate[J]. Bulletin of JSME, 1984, 27(232):2142−2151.

[11]Sakamoto H, Arie M. Vortex shedding from a rectangular prism and a circular cylinder placed vertically in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 1983, 126: 147−165.

[12]Zhou Y, Zhang H J, Yiu M W. The turbulent wake of two side-by-side circular cylinder[J]. Journal of Fluid Mechanics,2002, 458: 303-332.

[13]Hu J C, Zhou Y. Flow structures behind two staggered circular cylinders. Part 2. Heat and momentum transport[J]. Journal of Fluid Mechanics, 2008, 607: 81−107.

[14]Reynolds W C, Hussain A K M F. The mechanism of an organized wake in turbulent shear flow. Part 3. Theoretical model and comparisons with experiments[J]. Journal of Fluid Mechanics, 1972, 54: 263-288.

[15]Zdravkovich M M. Flow around circular cylinder. vol 2:Applications[M]. New York: Oxford University Press, 2002:726−728.

(编辑 杨幼平)

Three dimension characteristics of finite-length bluff body wake

WANG Han-feng

(School of Civil Engineering and Architecture, Central South University, Changsha 410075, China)

The wake flow behind a finite-length cylinder with aspect ratio of 3, 5 and 7 was measured using X-wire.Phase-averaged technique was applied. All experiments were conducted in a low-speed wind-tunnel atRed=3 500. It is found that the boundary layer on the wall and the free-end downwash flow make the near wake highly three dimensional.This three-dimensionality is clearly observed at 10d(dis the cylinder width) downstream from the cylinder. ForH/d=3,the phase-averaged fluctuation velocity and the power spectra are similar in all spanwise measurement locations. AsH/d=5 and 7, the periodicity of the wake is the most pronounced at the mid-span, and the phase-averaged fluctuation velocity is twice bigger than that near the free-end and wall.

wake; vortex street; hot-wire anemometer; phase average

O351.3

A

1672−7207(2011)02−0495−06

2010−02−26；

2010−04−16

国家自然科学基金资助项目(50208019)；中南大学自由探索计划项目(201012200215)

王汉封(1976−)，男，河南开封人，博士，副教授，从事流动的测量与诊断以及流动所诱发振动的研究；电话：13875856504；E-mail:wanghfme@gmail.com