抗滑桩加固边坡稳定性及影响因素的有限元分析

陈乐求，杨恒山，林杭

(1. 湖南理工学院 土木建筑工程学院，湖南 岳阳，414006；2. 中南大学 资源与安全工程学院，湖南 长沙，410083)

抗滑桩加固边坡稳定性及影响因素的有限元分析

陈乐求1，杨恒山1，林杭2

(1. 湖南理工学院 土木建筑工程学院，湖南 岳阳，414006；2. 中南大学 资源与安全工程学院，湖南 长沙，410083)

通过Fortran95语言编制边坡在抗滑桩加固情况下的稳定性程序(FPS)，并与商业软件FLAC3D的计算结果进行对比，以验证程序的正确性及优越性；然后，通过抗滑桩支护参数对边坡稳定性的影响进行分析。研究结果表明：(1) 当桩长较小时，抗滑桩设置在边坡中下部对稳定性最有利，当桩长较大时，抗滑桩设置在边坡中间对稳定性最有利；(2) 桩长对于边坡安全系数的影响程度与抗滑桩布置的位置有关，当抗滑桩位于坡顶或者坡脚时，桩长的变化对于安全系数的影响很小；而抗滑桩位于边坡坡面中央时，在桩的长度达到临界桩长之前，边坡的安全系数与桩长呈显著的线性关系；(3) 随着桩长的不断增大，潜在滑动面逐渐向边坡内部移动，破坏模式由浅层滑动变为深层滑动，安全系数也不断增大；但当桩长达到一定程度后，边坡的临界滑动面转移到临坡面位置。

边坡；抗滑桩；有限元；稳定性；影响因素

抗滑桩在边坡加固工程中广泛使用。人们以往主要采用极限平衡法研究边坡稳定性以及抗滑桩受力情况[1−4]。该方法需对桩土受力以及边坡滑动面进行假设，无法清晰反映边坡－抗滑桩的耦合效应以及边坡的滑移特征，并且由于桩和岩土介质具有不同的弹性模量、重度和强度，势必引起应力分布的非均匀化和进入塑性极限的不同步性，给边坡的稳定分析带来了很大困难[5]。近年来，随着计算机技术的不断发展，数值分析方法在边坡稳定性分析中逐渐得到应用[6−9]，该法不受边坡几何形状不规则和材料不均匀性的限制，如：Jeong等[6−7]利用极限平衡法和有限差分软件FLAC3D 分析了边坡－抗滑桩系统的稳定性；韦立德等[5]利用FLAC3D计算软件，根据抗剪强度折减弹塑性数值方法分析了含抗滑桩边坡稳定性优化问题。这些研究通常采用商业软件进行分析，而对于边坡源程序的开发研究尚显不足。商业软件如同1个黑箱子，设计者输入参数，然后，得到相应的计算结果，但其计算过程并不明确，并且以往的研究一般针对边坡的安全系数，而对滑动面变化情况的研究较少。在此，本文作者采用Fortan95语言编制边坡在抗滑桩支护情况下的有限元程序，并与有限差分法的计算结果进行对比，讨论抗滑桩支护参数的变化对边坡安全系数和滑动面的影响。

1 程序编制

Smith等[10]利用Fortran95语言编制了二维边坡稳定性分析的有限元程序，但该程序只能分析边坡在无支护情况下的稳定性，还无法实现结构单元如桩单元在支护情况下边坡的稳定性。为了进一步完善该程序的适用性，将采用 8节点矩形单元(8-node square quadrilaterals)和2节点桩单元，建立抗滑桩支护情况下边坡稳定性的分析程序(命名为FPS)，具体步骤如下：

(1) 建立边坡和抗滑桩几何模型。由于抗滑桩设置后，桩底可能与边坡单元节点无法重合，因此，需对边坡单元的节点坐标进行调整，如图1所示。

(2) 建立边坡单元刚度矩阵k1和桩单元刚度矩阵k2，然后，改变桩土结合处的边坡单元的刚度矩阵，如图2所示。从图2可以看出：每个边坡单元对应2个桩单元pi和pi+1。

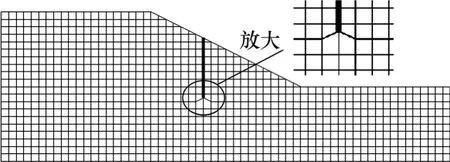
图1 抗滑桩支护边坡模型图Fig.1 Numerical model for slope with pile reinforcement

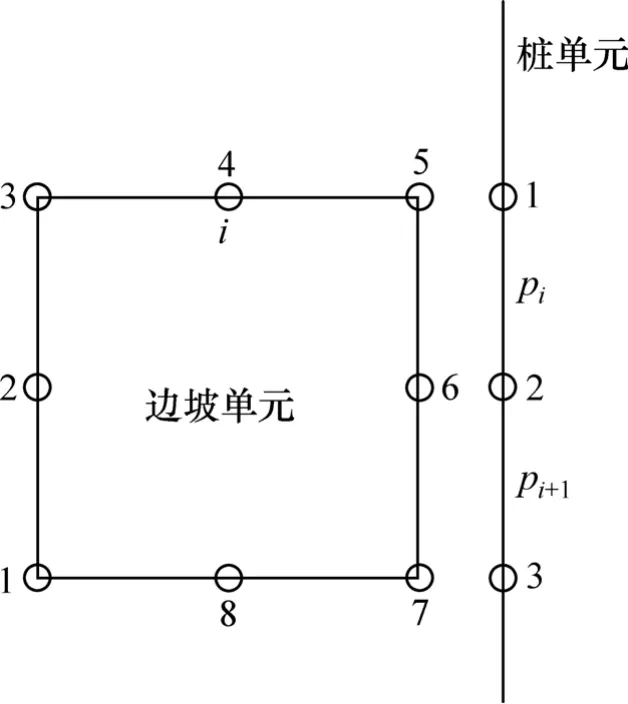
图2 桩土单元节点编号Fig.2 Number of slope element and pile element

(3) 利用单元刚度矩阵建立边坡整体刚度矩阵，施加外荷载，设置模型边界条件，进行求解。采用Mohr-Coulomb线性准则描述单元的破坏特征；边坡的安全系数定义为强度储备安全系数，其计算方法为强度折减法[11−14]，即计算过程中采用二分法迭代折减系数，不断调整土体的剪切强度参数即黏结力c和内摩擦角φ，反复对边坡进行分析， 直至其达到临界失稳状态为止[15]，此时，对应的折减系数即为边坡的安全系数。使用强度折减法可直接得出边坡的稳定安全系数，不需要事先假设滑裂面的形式和位置，还可以得到各结点的位移矢量[16]，从而大致给出破坏面的位置；另外，此处定义的抗剪强度折减系数与极限平衡分析中的边坡稳定安全系数在本质上是一致的[17]。

2 程序验证

2.1 计算模型

为了验证本文所编制程序 FPS的正确性，将其

得到的结果与商业软件 FLAC3D在平面应变情况下的计算结果进行比较。首先，建立 FPS边坡计算模型(如图3所示)，该边坡高为10 m，坡比为1:2。土体计算参数为：容重20.0 kN/m3，弹性模量50.0 MPa，泊松比0.3，黏结力15.0 kPa，内摩擦角20.0°；抗滑桩计算参数为：直径0.62 m，弹性模量25.0 GPa。模型边界条件为：边坡底面固定约束，左右边界为水平约束，上部为自由边界。建立 FLAC3D平面应变计算模型，如图4所示，采用与FPS相同的几何和物理力学参数参数计算边坡在不同网格密度情况下的安全系数。

图3 具有910个单元、2 891个节点的边坡计算模型Fig.3 Calculation model by FPS with 910 elements and 2 891 grids

2.2 程序验证

分别采用 FPS和 FLAC3D计算边坡在有限长桩(假设有限长桩为 8 m)和无限长桩加固情况下的安全系数，如表1和表2所示(其中：Lx为桩设置位置和坡脚的水平距离；L为坡脚与坡顶之间的水平距离；F为安全系数)。从表1和表2可以看出：FPS的计算结果与 FLAC3D较密网格模型的计算结果较接近，从而验证了 FPS程序的正确性和有效性；另外，网格大小对于 FLAC3D的计算结果影响较大，并且FLAC3D计算所需的时间远大于FPS计算所需时间，如FPS计算1个模型所需的时间为2 min，而普通网格FLAC3D模型计算需要30 min，较密网格FLAC3D模型计算需要7 h。

图4 FLAC3D平面应变计算模型Fig.4 Calculation model by FLAC3D in plane strain mode

表1 桩长为8 m情况下FPS与FLAC3D计算得到的安全系数的对比Table 1 Comparison of factor of safety obtained by FPS and FLAC3D for slope reinforced by finite pile

表2 无限桩长情况下FPS与FLAC3D计算得到的安全系数的对比Table 2 Comparison of factor of safety obtained by FPS and FLAC3D for slope reinforced by infinite pile

3 参数影响分析

考虑到桩长的影响因素，在图3所示的计算模型基础上，加大地基的深度，为20 m，使其能够包括所有计算长度内的桩，其他计算参数均与图3中的相同。另外，假设桩身材料一定，仅变化桩长和桩的布设位置，讨论边坡稳定性情况。

分别改变桩布设位置Lx/L于0～1之间内变化，以及桩长于6～22 m内变化，得到边坡相应的安全系数，如图5所示。从图5可以看出：随着Lx/L的增大，安全系数均呈现先增大后减小的趋势；但是，当桩长l较小时，安全系数最大值出现在Lx/L=0.25的位置；随着桩长l的增大，安全系数最大值出现的位置逐渐稳定在Lx/L=0.5处。即桩长较小时，抗滑桩设置在边坡中下部对稳定性最有利；当桩长较大时，抗滑桩设置在边坡中间对稳定性最有利。

图5 抗滑桩位置对边坡安全系数F的影响Fig.5 Effect of pile location on slope safety factor

从图5还可以看出：桩长对于边坡安全系数的影响程度与抗滑桩打入的位置有关，当抗滑桩设置于坡顶或者坡脚时，桩长的变化对于安全系数的影响很小；而当抗滑桩设置于边坡坡面中央时，桩长的变化对于安全系数的影响最为显著。抗滑桩设置在坡面中内时，安全系数与桩长的关系如图6所示。从图6可以看出：存在一个临界桩长，当桩长超过该临界桩长时，继续增加桩的长度并不能提高边坡的安全系数，而在桩的长度达到临界桩长之前，边坡的安全系数与桩长呈显著的线性关系(其中，R为拟合相关系数)。

为了探讨抗滑桩长度变化过程中边坡滑动面的变化规律，通过计算得到边坡的位移矢量，如图7所示。然后，利用图形取点技术，确定不同桩长下的滑动面分布，如图8所示。从图8可以看出：受到抗滑桩的支挡作用，边坡潜在滑坡无法穿切抗滑桩，因此，潜在滑动面均绕过抗滑桩底部；随着桩长的不断增大，潜在滑动面逐渐向边坡内部移动，破坏模式由浅层滑动变为深层滑动，安全系数也不断增大；但当桩长超过14 m后，边坡的滑动面位置并不延续之前的趋势，而是发生突变，迅速靠近坡面，潜在滑动面剪出口位于抗滑桩顶部，由原先的深层滑动面转变为浅层滑动面。这是由于抗滑加入土体时，与土体形成复合结构，大大提高了土体的抗滑能力，因此，边坡的滑动面逐渐往坡内移动；但当桩长度达到一定程度时，复合体的范围较大，此时向内移动的滑动面安全系数大于临坡面的滑动面安全系数，从而使边坡的临界滑动面转移到临坡面位置，继续增加桩长，滑动面位置并不发生变化。

图6 抗滑桩设置在坡面中央时安全系数F与桩长l的关系Fig.6 Relationship between slope safety factor with pile length when pile is driven at middle of slope surface

图7 边坡位移矢量图Fig.7 Displacement vector of slope

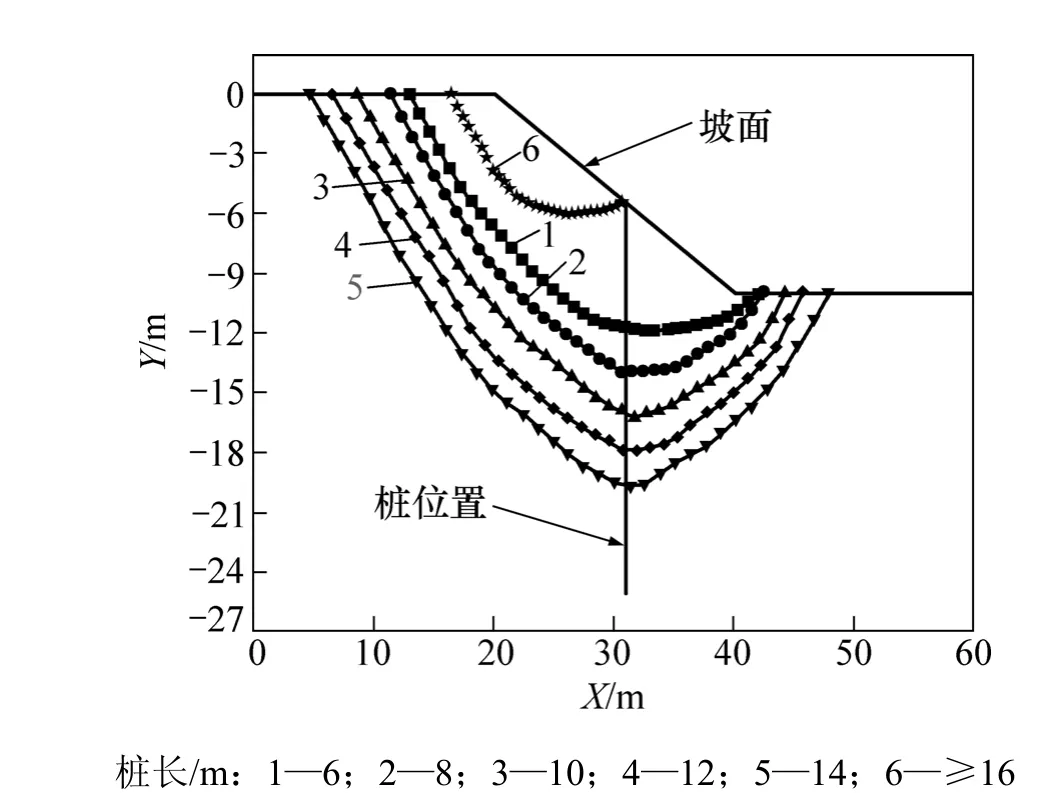
图8 边坡滑动面分布Fig.8 Distribution of slope slip plane

4 结论

(1) 通过Fortran95语言编制边坡在抗滑桩加固情况下的稳定性程序，并通过与FLAC3D软件的计算结果进行对比，验证了程序的正确性。

(2) 当桩长较小时，抗滑桩设置在边坡中下部对稳定性最好；当桩长较大时，抗滑桩设置在边坡中间对稳定性最好。

(3) 桩长对于边坡安全系数的影响程度与抗滑桩打入的位置有关：当抗滑桩设置于坡顶或者坡脚时，桩长的变化对于安全系数的影响很小；而当抗滑桩设置于边坡坡面中央时，在桩的长度达到临界桩长之前，边坡的安全系数与桩长呈显著的线性关系。

(4) 随着桩长的不断增大，潜在滑动面逐渐向边坡内部移动，破坏模式由浅层滑动变为向深层滑动，安全系数也不断增大；但当桩长达到一定程度后，边坡的临界滑动面转移到临坡面位置。

[1]陈祖煜. 土质边坡稳定性分析[M]. 北京: 中国水利水电出版社, 2003: 12−16.

CHEN Zu-yu. Analysis of soil slope stability[M]. Beijing:Chinese Water Conservation and Electricity Press, 2003: 12−16.

[2]Ito T, Matsui T. Methods to estimate lateral force acting on stabilizing piles[J]. Soils and Foundations, 1975, 15(4): 43−59.

[3]Ito T, Matsui T, Hong W P. Design method for stabilizing piles against landslide-one row of piles[J]. Soils and Foundations,1981, 21(1): 21−37.

[4]Hassiotis S, Chameau J L, Gunatatne M. Design method for stabilization of slopes with piles[J]. Journal of Geotechnical and Geo-environmental Engineering, ASCE, 1997, 123(4): 314−323.

[5]韦立德, 杨春和, 高长胜. 基于三维强度折减有限元的抗滑桩优化探讨[J]. 岩土工程学报, 2005, 27(11): 1350−1352.

WEI Li-de, YANG Chun-he, GAO Chang-sheng. Optimization of slide-resistant piles based on strength reduction method with 3D FEM[J]. Chinese Journal of Geotechnical Engineering, 2005,27(11): 1350−1352.

[6]Jeong S, Kim B, Won J, et al. Uncoupled analysis of stabilizing piles in weathered slopes[J]. Computers and Geotechnics, 2003,30(8): 671−682.

[7]Won J, You K, Jeong S, et al. Coupled effects in stability analysis of pile-slope systems[J]. Computers and Geotechnics, 2005,32(4): 304−315.

[8]Chow Y K. Analysis of piles used for slope stabilization[J].International Journal for Numerical and Analytical Methods in Geomechanics, 1996, 20(9): 635−646.

[9]Poulos H G, Chen L T. Pile response due to excavation-induced lateral soil movement[J]. Journal of Geotechnical and Geo-environmental Engineering, ASCE, 1997, 123(2): 94−99.

[10]Smith I M, Griffiths D V. Programming the finite element method[M]. 3rd ed. Chichester: Wiley, 1998: 76−83.

[11]林杭, 曹平, 宫凤强. 位移突变判据中监测点的位置和位移方式分析[J]. 岩土工程学报, 2007, 29(9): 1433−1438.

LIN Hang, CAO Ping, GONG Feng-qiang. Analysis of location and displacement mode of monitoring point in displacement mutation criterion[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1433−1438.

[12]Ugai K, Leshchinsky D. Three-dimensional limit equilibrium and finite element analysis: A comparison of result[J]. Soils Found, 1995, 35(4): 1−7.

[13]林杭, 曹平. 锚杆长度对边坡稳定性影响的数值分析[J]. 岩土工程学报, 2009, 31(3): 470−474.

LIN Hang, CAO Ping. Numerical analysis for the effect of cable length to the stability of slope[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(3): 470−474.

[14]Dawson E M, Roth W H, Drescher A. Slope stability analysis by strength reduction[J]. Geotechnique, 1999, 49(6): 835−840.

[15]林杭, 曹平, 李江腾, 等. 边坡临界失稳状态的判定标准分析[J]. 煤炭学报, 2008, 33(6): 643−647.

LIN Hang, CAO Ping, LI Jiang-teng, et al. Analysis of the standards for critical failure state of slope[J]. Journal of China Coal Society, 2008, 33(6): 643−647.

[16]LIN Hang, CAO Ping, GONG Feng-qiang, et al. The directly searching method for slip plane and its influential factors based on the critical state of slope[J]. Journal of Central South University of Technology, 2009, 16(1): 131−135.

[17]Griffiths D V, Lane P A. Slope stability analysis by finite elements[J]. Geotechnique, 1999, 49(3): 387−403.

(编辑 陈灿华)

Finite element analysis for slope stability and its influencing factors with pile reinforcement

CHEN Le-qiu1, YANG Heng-shan1, LIN Hang2

(1. Department of Construction and Engineering, Hunan Institute of Science and Technology, Yueyang 414006, China;2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

A program named FPS was compiled with Fortran95 for the slope stability analysis with pile reinforcement,the results from FPS were compared with those from commercial software FLAC3D for validation, and the efficiency of FPS was discussed. Then the influences of the pile reinforcement parameters on the slope stability were studied. The results show that (1) when the pile length is shorter, it is suggested to drive pile at the lower part of slope; while the pile length is longer, it is suggested to drive pile at the middle of slope surface; (2) the effect of pile length on slope safety factor is related to pile location; when the pile is driven at the slope vertex or slope toe, the pile length has little effect on the slope safety factor; while the pile is driven at the middle of slope surface and before the pile length reaches the critical pile length, the safety factor increases greatly with the pile length in the linear relationship; (3) with the increase of pile length, the slope potential slip plane moves gradually to the inner place, failure mode of slope changes from shallow slipping to deep slipping, and the slope safety factor increases as well; but when the length of pile reaches some magnitude, the potential slip plane moves close to slope surface.

slope; pile reinforcement; finite element; stability; influencing factors

TU457

A

1672−7207(2011)02−0490−05

2010−01−15；

2010−03−20

湖南省研究生创新基金资助项目(1343-74236000014)；长沙理工大学道路灾变防治及交通安全教育部工程研究中心开放基金资助项目(KFJ100306)

陈乐求(1980−)，男，湖南岳阳人，博士，讲师，从事岩土工程数值模拟研究；电话：18707309648；E-mail：chenleqiu2010@126.com