电力系统暂态稳定分析的探讨

路潇，龙燕，谭兴平

(解放军后勤工程学院，重庆401311)

随着电力系统的发展，互联电力网络变得越来越大。如此的发展趋势在给电力系统以巨大的技术和经济效益同时，也使得稳定性破坏事故所波及的范围更加广泛，电力市场的日益开放会使运行方式更加灵活多变，对稳定性的实时性判断要求更高。因此，准确、快速地分析电力系统在大扰动下的暂态稳定行为，必要时采取适当的控制措施，以保证系统对暂态稳定性的要求，是电力系统设计及运行人员最重要也是最复杂的任务之一。

1 暂态稳定问题的数学描述

IEEE对暂态稳定的定义如下:对于某一特定的稳定运行状态，以及对于某一特定的扰动，如果在扰动后系统可以达到一个可以接受的稳定运行状态，则对此初始状态而言在此扰动下系统是暂态稳定的，否则是暂态不稳定的［1］。在大扰动前后，系统状态变化的数学模型用三个非线形微分方程组描述:

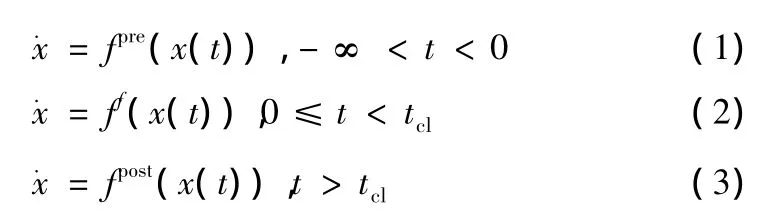
其中x(t)是系统的状态变量。

在故障前，系统处于稳态xpres，这是故障前系统(1)的稳定平衡点。当t=0时，系统发生故障，至t=tcl时故障清除。暂态稳定分析需要研究故障清除以后系统能否收敛到故障后系统(3)的稳定平衡点xposts。记故障清除时刻的系统状态为x(tcl)，若，则系统是稳定的，若则系统是不稳定的。

2 暂态稳定问题的分析方法

2.1 时域法

电力系统是一个强非线形系统，通常用一组非线性微分方程组来描述状态量，同时还有反映网络结构的代数方程组，电力系统可以用非线性方程组和代数方程组来描述。

时域仿真法是暂态稳定分析基本方法，它以稳态工况或潮流解为初值，对上述方程组联立求解或交替求解，逐步求得状态量和代数量，并根据发电机的转子摇摆曲线来判定系统在扰动下能否保持同步。

目前时域仿真法主要采用的数值计算方法包括显式积分法和隐式积分法。前者包括欧拉法、龙格－库塔法和线形多步法等。后者包括改进的欧拉法和隐式积分法。欧拉法的精度低，数值稳定性较差，一般适用于简单模型和较短的暂态持续时间。龙格－库塔法拟合了泰勒级数的高阶项，具有比较高的精度，数值稳定性好。它的缺点是计算量大，计算速度慢。线形多步法精度高，运算量比龙格一库塔法小，但计算结果受初始值的影响较大，需要选择适当的起步算法来保证其精度。改进的欧拉法用隐式积分校正欧拉法的结果，精度比欧拉法有所提高。隐式梯形积分法在联立求解微分一代数方程时可以消除交接误差，具有较好的数值稳定性，可以采用较大的步长。

虽然时域仿真法可以考虑电机的详细模型，而且能够得到足够准确的结果，但是随着网络规模的扩大，时域仿真法的计算量将很大，计算速度不能满足在线监测和控制的要求，并且其不能定量给出系统的稳定裕度。所以对电力系统暂态稳定研究致力于寻找一种快速、准确、实用的暂态分析算法。

2.2 直接法

直接法可以定量度量稳定程度，计算速度快，可用于在线稳定性分析。典型的直接暂态稳定方法有三种。

2.2.1 PEBS法

势能边界曲面PEBS法的着眼点在于沿着故障轨迹去寻找势能界面，从而确定临界切除能量。其稳定判据的基本思想是以持续故障轨线代替临界轨线，在角度空间的投影达到事故后系统PEBS的出口点EP，用出口点处的恒值能量曲面近似局部稳定边界。

因此，持续故障轨迹模拟精度的高低对临界能量的影响很大，同时因为要在多机系统环境下计算转子角随时间的变化，直到势能达到最大点，所以会影响计算速度。本文应用文献［2］所采用的基于Taylor级数动态步长控制方法，可以最大限度的增长持续故障轨迹模拟的步长，减少模拟区间数，提高计算效率。

2.2.2 BCU法

BCU方法是建立在现代非线性动力学系统理论基础之上的一种方法，它是位能边界曲面PEBS法与主导不稳定平衡点CUEP方法的有效结合。文献［3］导出了事故后稳定平衡点的吸引域的完全拓扑特征。特定故障下的主导不稳定平衡点，简称CUEP，其稳定流形包含故障时轨线的出口点。以EP为初值，积分事故后梯度系统，直至一个最小梯度点MGP，再以MGP为初值，解功率平衡方程得到梯度系统的CUEP，仅需补充一个零向量即可得到原始系统的CUEP。

对于一般电力系统模型，在高维状态空间中很难求取CUEP，文献［4］提供了下面的实用解法:

(1)运用变阶步长的隐式Adams—Bashforth—Moulton方法求解故障时的轨线以及EP;

(2)以EP为初值，运用变阶变步长的Gear法求解事故后梯度系统轨迹至MGP点;

(3)以MGP为初值，用牛顿法迭代求解功率平衡方程与网络方程得到CUEP。

在出现CUEP求解发散或收敛到错误的UEP情况时，文献［5］提出了一种校正梯度系统积分轨线方法，即阴影法。其基本思想是当梯度系统积分轨线偏离PEBS时，每隔四五步，运用点积判据校正，将其拉回PEBS。

2.2.3 EEAC法

扩展等面积准则的基本概念是在故障扰动下，假定电力系统的机组分为临界机组及非临界机组两群，然后对这两机组分别用等值机进行两机动态等效，进而等值为单机无穷大母线系统，从而系统的暂态稳定可用面积定则进行评定(图1)，从初始功角到故障清除时刻的功角这一故障时段，发电机转子加速，过剩转矩对转子相对角位移所做的功，用加速面积表示，故障清除后，发电机转子减速，制动转矩对转子角相对位移所做的功，用减速面积表示，如果系统稳定，则加速面积必小于最大可能的减速面积。文献［6］扩展等面积法进行了详尽的分析。

图1 面积定则

2.2.4 PEBS，BCU，EEAC三种方法的优缺点

PEBS法应搜索与故障切除时间相对应的系统转子角轨迹，即临界轨迹上势能达到最大值的点，并以此作为临界能量，但临界切除时间不可预知，因此采用持续故障轨迹来代替临界轨迹，并以其上搜索的势能最大值为V(主导不平衡点处的临界位能)的临界值，会造成误差。

BCU方法要求先判别系统失稳模式，但由于故障初始时系统信息不足，有可能发生失稳模式判断失误，因而引起误差。改进BCU方法在于提高出口点(EP)及计算主导不稳定平衡点(CUEP)的精度和效率，并保证可靠判别。故障发生在机端时，采用PEBS方法判别稳定性，既可保证可靠判别，又比BCU方法节约时间;在网中发生故障时采用BCU方法分析，可保证可靠判别，虽然稍为保守，但避免了冒进的结果。

EEAC方法的突出优点是计算速度快，但该方法有赖于正确识别临界机群，需要从临界故障清除时间中选择最小的一个作为系统的临界稳定条件。需要假定同一机群内各发电机转子角相等，并据此把系统等值为单机无穷大系统，这种假定使得结果可能偏保守，也可能偏冒进。

暂态能量函数方法(直接法)以其能够定量估价系统稳定性、适合于灵敏度分析以及计算快速见长，但在模型能力上在一些控制装置方面仍然存在限制，因而成为仿真方法的一种补充，井非代替仿真方法。即便在动态安全分析领域，仍然需要开展多种方法(包括仿真方法)的应用研究。

2.3 动态安全域法

动态安全域(DSR)法是动态安全分析与暂态稳定控制中的一种新的方法。动态安全域法是定义在事故前注入空间上的一个开集，对于域中的任何一个点，在发生给定事故后均可保证系统的暂态稳定性。这不仅对于校正性控制、紧急控制和恢复控制的决策有用，而且为电力市场下的输电安全定价提供了便利的分析工具［4］。

动态安全域的构成方法是定义在注入功率空间Rn上的集合。一个具体事故的动态安全域是由事故前注入功率空间上能保证该事故发生后系统暂态稳定的所有的点组成的集合。获得了超平面形式的安全域边界之后，稳定约束变成了注入功率线性组合的不等式，其表达式:

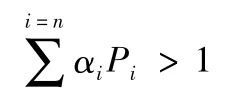
其中:i为超平面系数;Pi为节点注入功率;n为系统中注入的节点数［5］。

它的优点有:加深对电力系统安全稳定域边界的性质与规律的认识，从而减少误判断;在计算不确定性的安全性评估时不必用蒙特卡罗法，可用解析法，从而可使计算量降低若干个数量级，且可使各种与调度相关的最优化问题中稳定性约束的计算变得十分简易。因此，安全域为安全性监视、评估与优化，以及紧急控制的决策提供了十分有力的解析工具。

它的主要缺点是:电力系统安全域实际上是一个超曲面的多维空间，实际中很难描述。对多机系统的判别准确度不高，在解决多机系统中却存在计算数目较多，难以在大系统中应用。

3 结束语

综上所述，目前电力系统暂态稳定分析的各种方法都存在着各自的缺点，主要集中在计算精度、计算速度、模型适应性3个方面。因此，如何不依赖于模型参数，快速地对电力系统的稳定性作出准确地评估，给出精确的稳定域，以满足暂态稳定的实时性要求，实现暂态稳定的在线应用，是从事电力系统稳定分析与控制的运行人员及研究者亟待解决的问题

［1］倪以信，陈寿孙，张宝霖．动态电力系统的理论和分析［M］．北京:清华大学出版社，2002

［2］白雪峰，姜彤，郭志丹．基于Taylor级数法动态步长控制的暂态能量函数法［J］．电力自动化设备，2004，24(3)

［3］Chiang H．D，Wu FF，Varaiya P．A BCU Method for Direct A-nalysis of power system Transient Stability，In:IEEE/PES Summer Meeting San Diego:1991，423－424

［4］Ejebe G C，Irisarri G D，Tinney W F etal A Spare Fomulation and implementation of the transient Energy Function Method for Dynamic Security Analysis Electrical Power＆Energy Systems，1996，18(1):3－6

［5］赵庆生．基于能量分析的电力系统暂态稳定紧急控制新方法［D］．上海交通大学，2004

［6］周勤勇．扩展等面积法的研究及其在电力系统分析综合程序中的程序开发［D］．中国电力科学研究院，2003

［7］曾沅，余贻鑫．电力系统动态安全域的实用解法［J］．中国电机工程学报，2003，23(5)

［8］刘辉，余贻鑫．基于实用动态安全域的电力系统安全性综合控制［J］．中国电机工程学报，2005，25(20)