Aln（n=2～22）团簇构型研究

姚树文,侯振雨,崔乘幸

（河南科技学院,河南新乡453003）

团簇作为各种物质由原子、分子向大块物质转变过程中出现的特殊相,代表了凝聚态物质的初始状态,团簇研究的基本问题是弄清团簇如何由原子、分子发展而成以及随着这种发展,团簇结构和性质的变化.Aln团簇近年来引起了人们广泛的研究兴趣,因为Aln团簇的电子结构简单,且随着原子数增加,表现出金属的过渡性：如Al的化合物或粉状颗粒不具有导电性,而Al晶体却能导电.因此在过去的20多年里,广大科学工作者对此进行了大量的理论和实验研究[1].

团簇是由几个、几十个到几千个原子或分子所构成的集合体,其尺寸一般为埃数量级.团簇的各类电子性质和各种量子效应都与其它材料有显著的不同,有一系列既不同于原子、分子又不同于大块固体的物理效应.金属团簇对比其它团簇来讲是非常重要的,如：金属团簇经常可用来做化学反应的催化剂,所以在实验和理论上都得到了广泛的重视.团簇的特性随着团簇尺寸大小的变化有很多吸引人的地方,不管是金属或非金属原子组成的团簇的性质都随团簇的原子数目和结构特点的变化而变化,体现出不同的金属性和非金属性,磁化或非磁性等等,随团簇中原子数增加的变化是团簇性质研究的重要部分.人们发现,具有特殊个数（幻数）的原子组成的团簇具有显著的稳定性.幻数是团簇的一个重要物理特征,但团簇的幻数非常复杂,每种元素的团簇幻数都不相同,研究的Aln团簇由于电子结构简单,导电性随着原子数目变化而改变,近年来受到了材料科学工作者的广泛关注[2].

量子化学计算可以获得团簇体系的电子波函数,通过这些电子波函数可以求算偶极矩、极化率等团簇性质的计算,但是一方面由于数学方法的局限,量子化学计算方法只能是一种近似计算,虽然能量的计算可以获得较好的结果,但是获得的电子波函数质量却很差,因而团簇性质计算的精度远远不及团簇体系能量的计算.另一方面改进量子化学计算方法以获得质量更好的电子波函数也是绝大多数量子化学家们目前面临的挑战之一[3].

1 计算方法

1.1 实验方法

（1）利用Gaussian 03的编程软件,写出Aln团簇的Z-matrix形式,从而构造出Aln团簇的构型.

（2）用DFT法计算：用Gaussian 03中DFT的B3LYP方法,6～31 G基组计算Aln团簇的结合能并比较Aln团簇构型、HOMO-UMO能隙及平均键长间的关系.

1.2 构造的前9（n=2～10）种Aln团簇的构型

构型见图1所示.

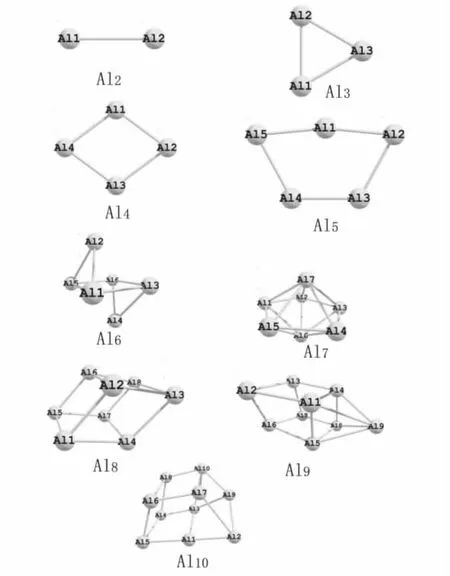
图1 Aln（n=2～10）团簇的计算模型

图1给出了优化后得到的Aln团簇原子数n=2～10的相对稳定的典型结构（初始Al-Al键长设为d=0.27 nm）,它们的构型是使用了DFT中的B3LYP方法,6～31 G基组进行优化后得到的.通常情况下,由于原子空间排布的不同,Aln团簇的构型也复杂多样,并且会有大量不同构型具有相同（或差别很小）的能量,故一般很难确定哪种状态是最稳定结构,所以研究能量整体极小点的构型是很重要的,还可以为以后研究Aln团簇与O2的反应及团簇其它反应提供参考[4].

2 结果与讨论

表1 Aln（n=2～22）团簇的各类能量

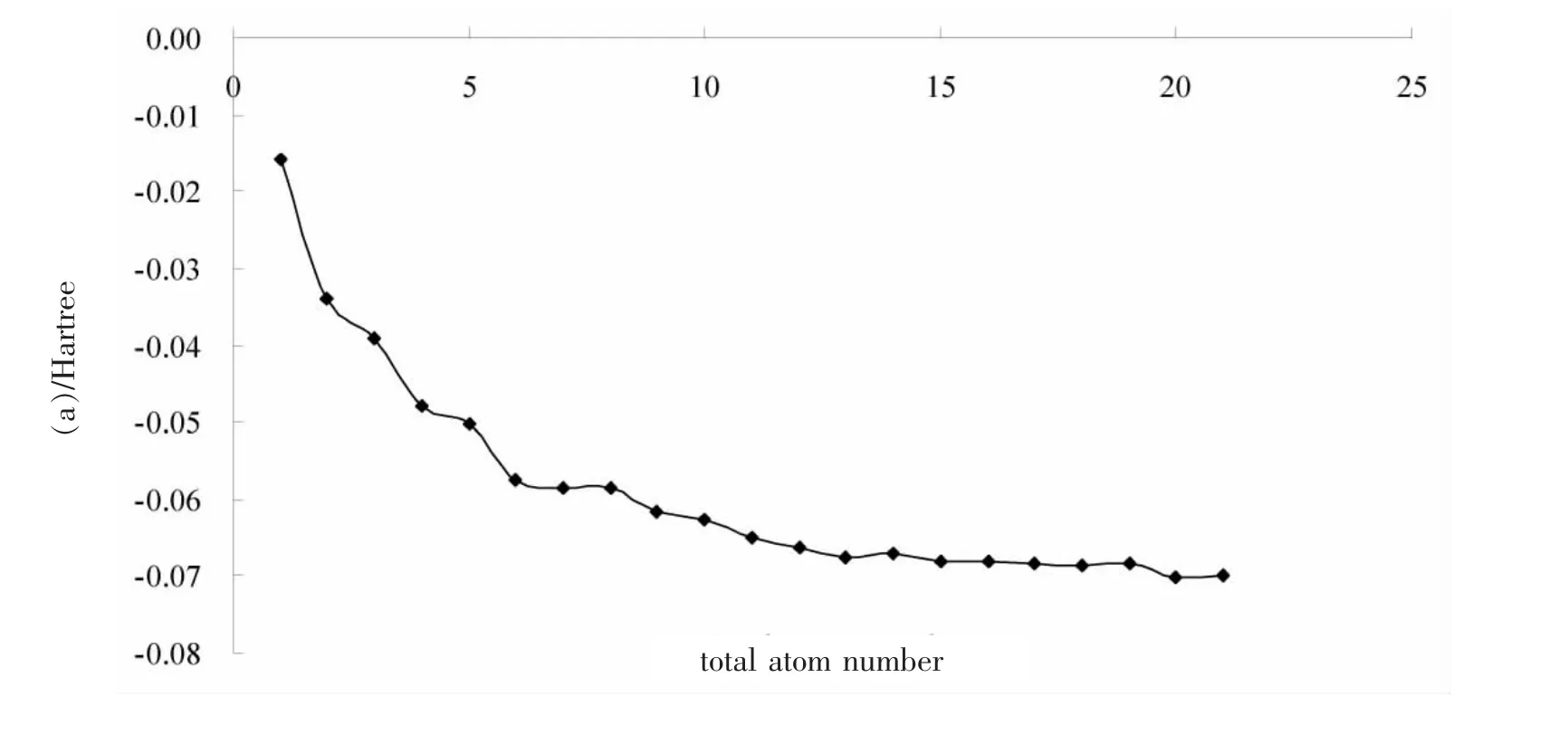
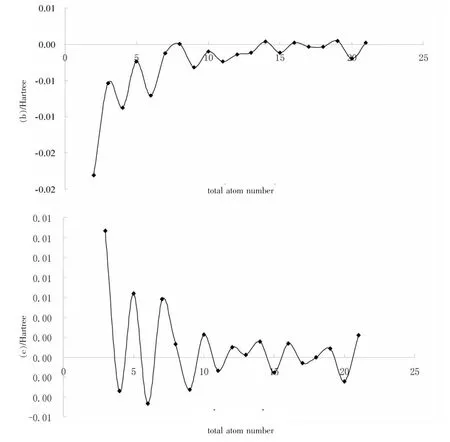
图2 Aln（n=2～22）团簇的结合能（a）、结合能的一阶差分（b）、结合能的二级差分（c）随团簇中总原子数n的变化关系

图2对Aln（n=2～22）团簇构型进行的各类能量分析,其中E（n）代表Aln团簇中平均每个原子的结合能,结合能定义为E（n）=[Etotal（Aln）-nE（Al）]/n,式中Etotal（Aln）为Aln团簇的总能量,E（Al）是Al自由原子能量；一阶差分定义为△E（n）=E（n）-E（n-1）,它描述了团簇丢失一个原子的能力；二阶差分定义为△2E（n）=E（n+1）+E（n-1）-2E（n）,在团簇物理中该二阶差分是一个能够敏感反映团簇稳定性的物理量.图2（a）显示,Aln团簇的平均每个原子的结合能从原子数n=2～5都是快速增加的,超过5个后才明显变缓,说明5个原子之后才足够形成较强的金属键,实际上n＞5后团簇都是金属键性质的,这从下面团簇的mHOMO-LUMO能隙图也可以看到.分析表明刚开始快速增长阶段对应结构上二维到三维的转变,然后则对应范德华键到共价键的转变.[5]显然,结合能曲线的变化轮廓与形成团簇原子的电子组态相关,也即与原子间的成键形式密切相关.由图2（a）可见,本研究计算的结合能E比实验值略高,而Rao等采用Gaussian程序DFT-GGA近似计算的E值则比实验值略低,但在整体上,三者的变化趋势一致,随着原子数n增加,结合能E值增大,其结构稳定性也相应随之增大,并且随着原子数n值越来越大,结合能E值增加的也相对缓慢.团簇结构稳定性也可采用团簇总能量相对于原子数n的二阶差分来表示,由图2（c）可见,与上面结合能E的变化趋势（图2（a））一致.[6]

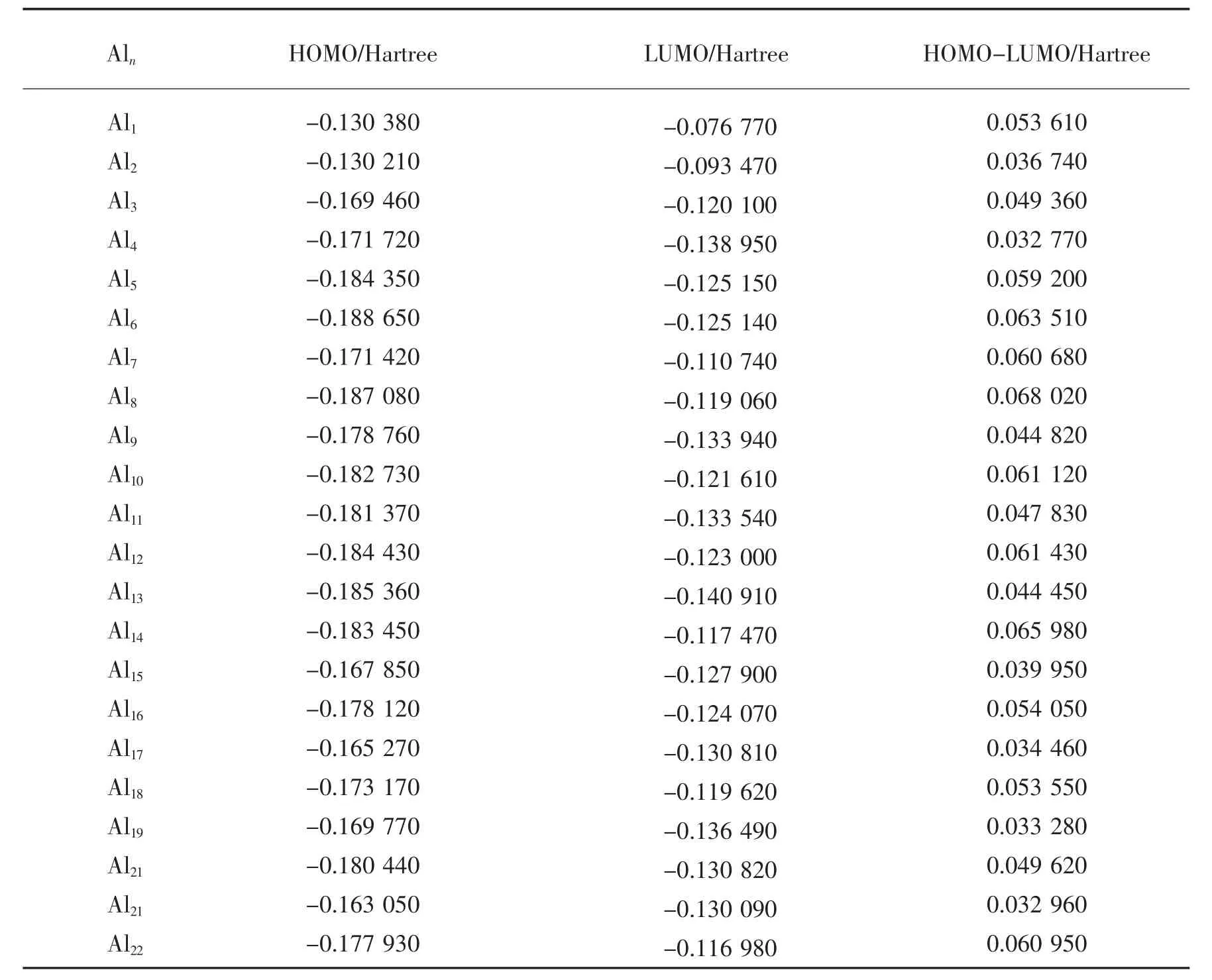
表2 Aln（n=2～22）团簇的HOMO-LUMO能隙

图3 Aln（n=2～22）团簇的HOMO-LUMO能隙随团簇原子数n的变化

图3中HOMO（Highest occupied molecular orbital）为最高分子占据轨道,LUMO（Lowest unoccupied molecular orbital）为最低分子非占据轨道.在分子中,HOMO上的电子能量最高,具有电子给予体的性质,所受束缚最小,所以最活泼,容易变动；而LUMO在所有的未占轨道中能量最低,最容易接受电子,因此这两个轨道决定着分子的电子得失和转移能力,决定着分子间反应的空间取向等重要化学性质.HOMO、LUMO统称为前线轨道,处在前线轨道上的电子称为前线电子.最先作用的分子轨道是前线轨道,起关键作用的电子是前线电子.这个分布的大小次序决定亲电试剂进攻各个原子位置的相对难易程度,即亲电反应最易发生在HOMO最大电荷密度的原子上；与此类似,亲核反应在各个原子上发生的相对次序由LUMO的电荷密度分布决定,亲核试剂最容易进攻LUMO电荷密度最大的原子.给电子基使得HOMO-LUMO能隙变宽,吸电子基使得HOMO-LUMO能隙变窄.从图3可见,对于原子数n≤5的Aln团簇,其HOMO-LUMO能隙值相对较大,显示其共价性的成键特点,而对于原子数n＞5的团簇,其成键特征已经是金属性.考虑到HOMO-LUMO能隙△EH-L随团簇尺寸或原子数的变化对团簇稳定性与电子结构演变能给出某些有用信息,如HOMO-LUMO能隙越大,则预示着相应团簇的稳定性越高,HOMO-LUMO能隙越小,团簇的稳定性越低[7].由于Al原子的最外层有3个电子,当Aln团簇中Al原子数n为奇数时有未配对的电子,而n为偶数时外层电子全部配对.由图3可见,当原子数n＞5时,原子数n为偶数时的HOMO-LUMO能隙△EH-L大于原子数n为奇数时的HOMO-LUMO能隙△EH-L,说明原子数n为偶数时Aln团簇的稳定性大于原子数n为奇数时Aln团簇的稳定性,这与实验结果及经验吻合较好.

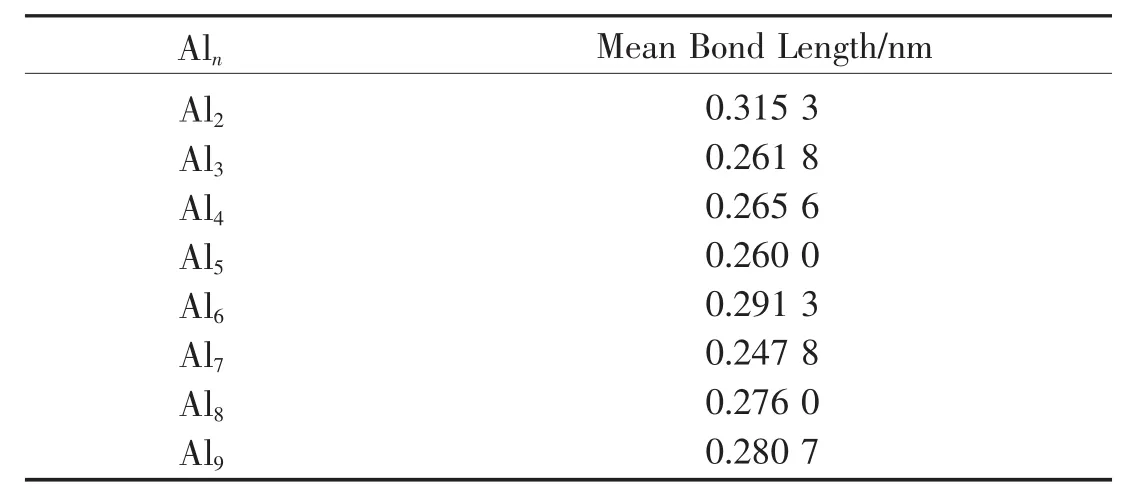
表3 Aln（n=2～9）团簇的平均键长（R）随团簇原子数n的变化

表3显示了n=2～9的Aln团簇中原子平均键长（R）随原子数n的变化,平均键长（式中Rij为在0.32 nm范围内i原子和j原子的距离.可以看到,团簇中原子间的平均键长越短,则团簇的相对稳定性越好.

3 结论

本文应用密度泛函理论（DFT）框架下的B3LYP方法,6～31G基组对Aln（n=2～22）团簇构型进行优化,得到了：①Aln（n=2～22）团簇的相对最低能量结构,及影响Aln团簇性质的主要因素是团簇的几何构型；②对团簇结构进行了相对稳定性的分析,其结合能随团簇中原子数n的增大而增大,结构稳定性逐渐增强；③讨论了团簇的HOMO-LUMO能隙,暗示了团簇中原子的成键特点随团簇原子数n的变化而变化,并且HOMO-LUMO能隙值越大,则团簇的稳定性越好；④本研究计算的结合能E、HOMO-LUMO能隙△EH-L及平均键长（R）和实验值以及前人的计算结果吻合很好,而且与目前关于Aln团簇构型的文献也基本相符,本研究所选的模型可靠,且计算条件与方法合适,因此采用分子动力学在此方面的研究是成功的.

∶

[1] 林秋宝,李仁全,文玉华,等.Wn（n=3-27）原子团簇结构的第一性原理计算[J].物理学报,2008,57（1）：181-185.

[2] 彭平,李贵发,郑采星,等.Aln（n=3,4,6,13,19）团簇的结构稳定性与形态演化[J].中国科学E辑技术科学,2006,36（9）：975-982.[3]李贵发,彭平,周惦武,等.n=2-13）团簇分裂机理的计算[J].中国有色金属学报,2008,18（3）：516-521.

[4] 李贵发,彭平,仇治勤,等.Aln（n=2-24,55）团簇结构特性的第一原理计算[J].中国有色金属学报,2006,16（5）：823-826.

[5] Rao B K,Jena P.Evolution of the electronic structure and properties of neutral and charged aluminum cluster：a comprehensive analysis[J].J Chem Phys,1999,111（5）：1890-1904.

[6] Ray U,Jarrold M F,Bower J E,et al.Photo dissociation kinetics of aluminum cluster ions：determination of cluster dissociation energies[J].J Chem Phys,1989,91（5）：2912-2921.

[7] Wang J L,Wang G H,Zhao J J.Density-functional study of Aun（n=2～22）clusters：Lowest-energy structures and electronic properties[J].Phys RevB,2002,66（3）：035418-035423.