瞬时对称分量法及其在故障暂态测距中的应用

高作毅 罗显通 黄翰

(1.重庆市电力公司璧山供电局，璧山 402760;2.四川电力设计咨询有限责任公司，成都 610016)

0 引言

对于三相系统，由于各相间存在电磁耦合，直接在相域进行故障计算十分困难。为简化计算，一般需要进行相模变换以实现解耦。常用的相模变换有对称分量变换、派克变换、克拉克(E.Clarke)变换，卡伦鲍厄(Karrenbauer)变换等［1～4］。其中对称分量法被广泛用于继电保护、故障分析、无功补偿、系统建模、系统辨识等电力系统各种领域。

传统的对称分量法定义在频域范围，处理三相电流、电压的相量，只适用于电力系统稳态分析。瞬时对称分量法定义在时域范围，利用电流、电压的瞬时值进行对称变换，因此可分析电力系统的暂态过程。文献［4］提出一种根据旋转磁场原理将参考坐标置于电机定子侧的瞬时对称分量变换，然而变换矩阵中仍采用复数相位因子，得出的序分量为复数变量。文献［5～6］在时域中用120°移相操作代替变换矩阵中的复数相位因子进行变换，其核心是借助锁相环(EPLL)提取出的基波相位实现移相，但锁相环的计算会带来一定的延时，不利于序分量的实时提取。文献［7］利用电压或电流瞬时值构造旋转相量，采用传统对称分量变换矩阵与旋转相量相乘求出以复数形式表示的序分量，最后提取其虚部得瞬时值。

本文提出的瞬时对称分量变换法，通过三角函数变换分解出旋转相量的实部和虚部，再利用简单的移相算法对三相电流、电压瞬时值进行相应的变换，从而获取各个序分量的瞬时值。将该法用于电力系统故障分析，能在故障暂态过程中快速计算故障距离，动模试验及matlab分析验证了该方法的有效性和实用性。

1 瞬时对称分量变换的基本原理

1.1 瞬时序分量的表示方法

设三相电流的瞬时值为幅值和相位不随时间变化的正弦周期信号，其表达式为

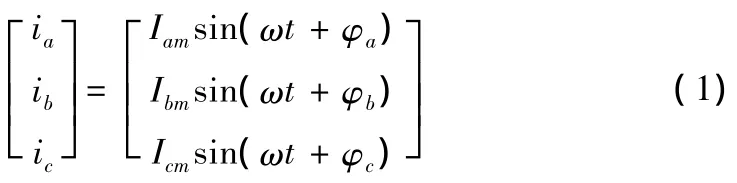
式中 ia、ib、ic分别为三相电流瞬时值;Iam、Ibm、Icm分别为三相电流的幅值;φa、φb、φc分别为三相电流的初相位。

由于对称分量法运用旋转相量进行变换，而ia、ib、ic对应的旋转相量分别为，其表达式为

以A相为例，则复平面上所对应的旋转相量图如图1所示。

图1 旋转相量

由对称分量法知，三相电流相量与其对称分量之间的关系为

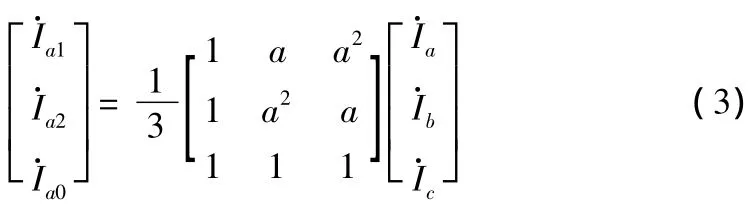
式(4)中ib120、ib240分别表示将B相电流瞬时值的相位向前移动120°和240°;ic120、ic240分别表示将C相电流瞬时值的相位向前移动 120°和 240°。

以B相电流瞬时值为例，运用三角函数分解法，将其相位前移120°可表示为

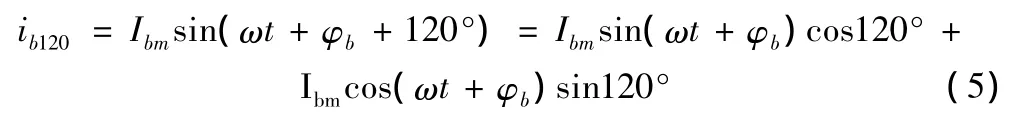
即

1.2 相量实部的求取

以B相电流为例，其瞬时值可表示为

即

移相变换得

又

则将式(9)代入式(10)可得

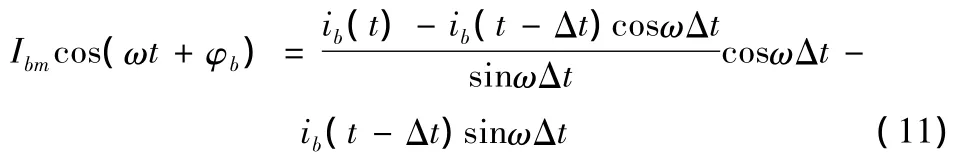
将式(11)代入式(6)可求出ib120。同理可求出ib240、ic120和ii240，最后将所得结果代入式(4)可得瞬时序分量的值。

2 基于瞬时序分量的暂态故障测距方法

2.1 基本思路

在分析三相对称系统的暂态过程时，通常借助对称分量变换将三相线路转换为单相线路求解。当线路上发生短路故障，利用故障点的序分量边界条件可方便的进行故障分析［8－14］。由于故障时系统电感电流和电容电压不能突变，将会产生除基波分量以外随时间衰减的高频分量和直流分量，传统的对称分量变换针对稳定周期信号的相量提取，对于故障暂态信号的提取存在较大的误差，而瞬时对称分量法能实时提取序分量瞬时值，有利于实时分析系统故障。本文以线路发生两相短路故障为例，提出一种利用瞬时序分量进行暂态故障测距的方法，基本思路是通过序分量边界条件建立故障网络时域微分方程，利用瞬时对称分量变换求出方程中的瞬时序分量，最后通过最小二乘法求解故障距离［15］。

2.2 暂态测距原理

图2为两相相间短路和两相短路接地故障。

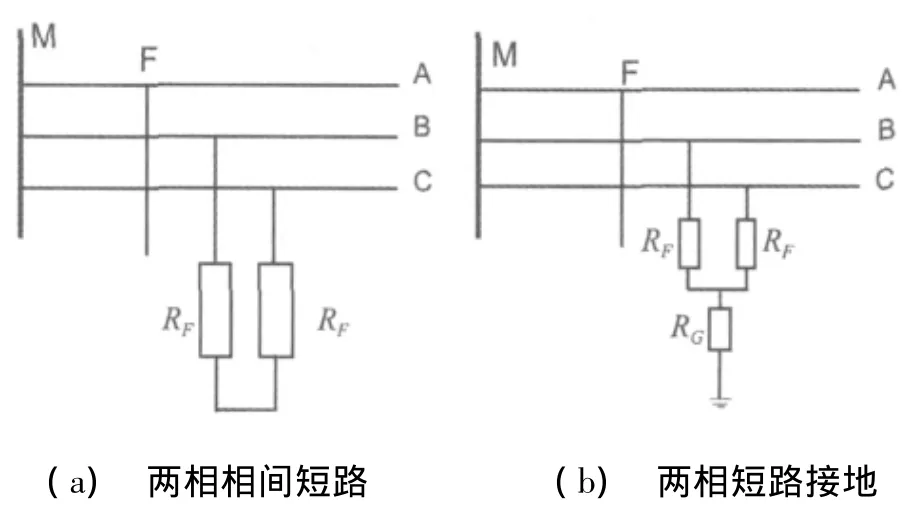
图2 两种短路故障模型

若忽略输电线路分布电容，则对于这两种故障模型 ，可分别写出正、负序网络的微分方程

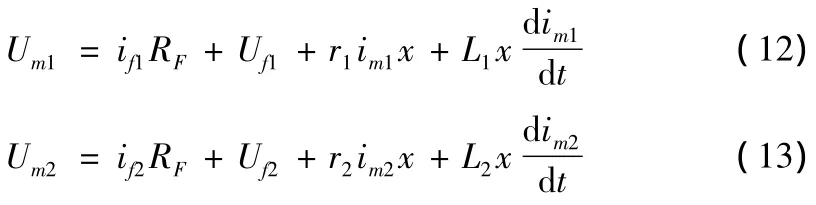
式(12)、(13)中 Um1、Um2、im1、im2分别代表测量端 M 处的正、负序电压和电流瞬时值;Uf1、Uf2、if1、if2分别代表 F处的正、负序电压和电流瞬时值;r1、r2、L1、L2分别为线路单位长度的正序、负序电阻和电感;x为测量点与故障点之间的距离。

图2中，两相相间短路故障的边界条件为Uf1－Uf2=0;两相短路接地故障的边界条件为Uf1=Uf2=Uf0。因此将式(12)、(13)左右两边分别相减，并考虑到正、负序电阻、电感参数分别相等，整理可得

由于故障点的电流不能直接检测，因此假设故障点各序电流的故障分量和保护安装处各序电流的故障分量具有相同的相位，即两者之间存在K倍关系，其中K为实数，其值由故障点两端的网络结构参数决定。采用该假设的原因有三点:其一，本文的研究对象为配电网，负荷侧的短路电流很小，可近似认为故障点短路电流为送电侧电流;其二，由叠加定理知线路上的故障电流为正常分量与故障分量的叠加，而短路点电流仅含故障分量，可近似认为与送电侧电流故障分量同相;其三，两相短路的接地电阻并不影响本文算法，而相间过渡电阻通常较小，对于本文假设所带来的误差不大。

根据假设将故障点的正、负序电流故障分量分别用测量点的正、负序电流故障分量表示

式(15)中im1N为系统正常运行时测量点的正序电流瞬时值;K1、K2为实数，考虑到正、负序网参数相同，因此K1=K2;将式(15)代入式(14)

式(16)中将K1RF和x作为未知量，理论上只需故障后的两个点即可确定故障位置，但考虑到减小偶然误差对测距精度的影响，应增加点数，运用最小二乘法辨识出故障距离。

3 动模试验验证

为了验证瞬时对称分量变换及其在故障暂态测距中的正确性和可行性，在输配电装备及系统安全与新技术国家重点实验室中进行了动模试验，其系统接线如图3所示。

图3 动模试验系统

此系统中，试验线路使用串联阻抗器代替，所模拟的线路全长为6km，其等效参数如下:r1=0.017Ω/km，X1=0.38Ω/km，r0=0.237Ω/km，X0=1.72Ω/km。电源由 220V 无穷大系统接入，经两组变压器将试验线路母线电压调整为1000V。利用中国电力科学研究院提供的DF1024便携式录波仪测量PT及CT二次侧电压、电流，并将波形数据导入Matlab中进行分析计算。图4为采样频率为5000Hz，线路末端发生BC相间短路时的故障录波图。运用本文所提出的瞬时对称分量法提取出正、负、零序分量，结果如图5、图6所示。

由图5和图6可以看出，在故障发生前，三相系统对称，只有正序分量存在，负序和零序分量基本为零;故障发生后，零序分量仍为零，波形中仅有正序和负序分量，与BC相间短路的边界条件一致。为进一步验证瞬时对称分量法的正确性，利用式(16)计算故障距离。由于故障后的衰减直流分量通常在一到两个周波后趋于零，这在图4中也可以看出，因此算法从故障发生一个周波后开始计算。由于方程中仅有两个未知参数，理论上只需取两组故障序分量值便可得到故障距离。但考虑到减小随机误差的影响，可选取10ms内的几组数据进行最小二乘优化，得出较为准确的故障距离。表1给出了不同故障距离下的测距结果;表2为不同采样频率下试验线路末端故障时的测距结果。表中测距误差计算公式为

测距误差=|测量距离－实际距离|/线路全长×100%

由表1可以看出，利用瞬时对称分量法提取的序分量能较为准确的测量故障距离，证明了本文所提出的瞬时对称分量法及故障暂态测距原理的正确性。由表2可以看出，随着采样频率的降低，测距误差相应增大，这是因为用差分代替求导所带来的截断误差会随采样频率降低而增大。

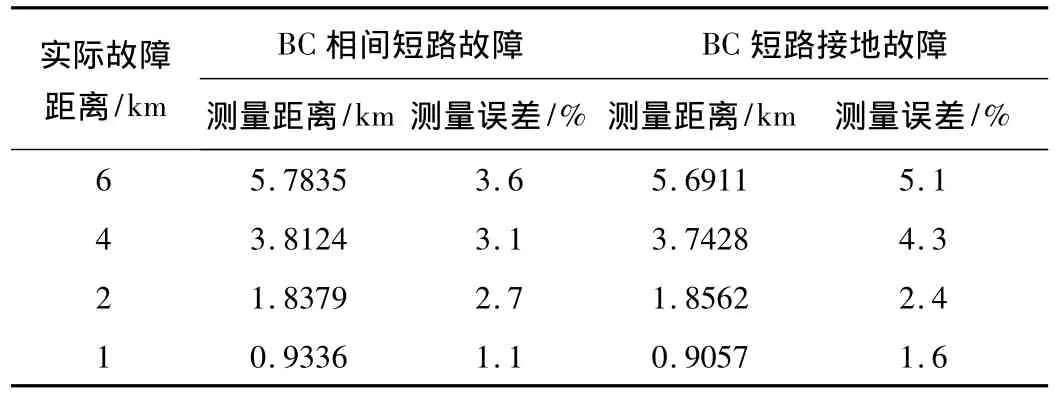
表1 不同故障距离下测距结果

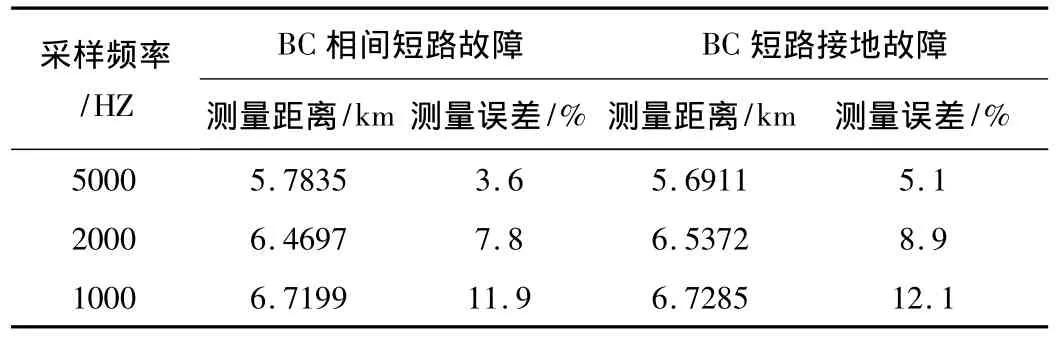
表2 不同采样频率测距结果

4 结论

本文提出了一种时域中在线计算序分量的瞬时对称分量变换法，并将其应用在故障暂态测距分析中，取得了良好的试验效果。

(1)针对传统对称分量变换结果为相量或复数变量，不利于电力系统实时暂态分析的缺陷，提出了基于移相操作和三角函数变换的瞬时对称分量法，所求出的瞬时序分量不仅能够应用于稳态分析，也能用于暂态分析。

(2)基于该理论，提出一种新型的暂态故障测距方法，思路是通过边界条件建立故障网络时域微分方程，将检测点的三相电压、电流转换为瞬时序分量后运用最小二乘法辨识出故障距离。

(3)通过动模试验波形分析及matlab数据计算，验证了所提方法的正确性。随着设备采样频率的提高，测距精度将得到改善。

［1］ Gerardus C.Paap.Symmetrical components in the time domain and their application to power network calculations［J］.IEEE Transactions on Power Systems，2000，15(2):522－528.

［2］ TAVARES M C，PISSOLATO J，et al.Mode Domain Multiphase Transmission Line Model-Use in Transient Studies［J］.IEEE Transactions on Power Delivery，1999，14(4):1533－1537.

［3］ 施围，郭洁.电力系统过电压计算［M］.北京:高等教育出版社，2006.

［4］ 诸骏伟.电力系统分析［M］.北京:水利电力出版社，1995.

［5］ Iravani MR，Karimi-Ghartemani M.Online estimation of steady state and instantaneous symmetrical components［J］.IEE Proc-Gener.Transm.Distrib，2003，150(5):616－622.

［6］ Masoud Karimi-Ghartemani，Houshang Karimi.Analysis of symmetrical components in time-domain［C］.The 48th Midwest Symposium on Circuits and Systems，Covington，Kentucky，USA，2005.

［7］ 袁旭峰，程时杰，文劲宇.改进瞬时对称分量法及其在正负序电量检测中的应用［J］.中国电机工程学报，2008，28(1):52－58.

［8］ 葛耀中.新型继电保护与故障测距原理与技术［M］.西安:西安交通大学出版社，1996.

［9］ 索南加乐，齐军，陈福锋，等.基于R-L模型参数辨识的输电线路准确故障测距算法［J］.中国电机工程学报，2004，24(12):119－125.

［10］ 梁振锋，康小宁，姚李孝，等.关于故障分量概念的讨论［J］.继电器，2007，35(1):37－46.

［11］ 吴萍，张尧.基于单端电气量的故障测距算法［J］.电力系统及其自动化学报，2003，15(4):5－7.

［12］ 束洪春，司大军，葛耀中，等.高压输电线路电弧故障单端定位时域法新解［J］.中国电机工程学报，2000，20(11):25－29.

［13］ 索南加乐，刘文涛，陈勇，等.基于R-L模型误差的自适应距离保护［J］.电力系统自动化，2006，30(22):66－72.

［14］ 王宾，董新洲，薄志谦，等.特高压长线路单端阻抗法单相接地故障测距［J］.电力系统自动化，2008，32(14):25－29.

［15］ 方崇智，萧德云.过程辨识［M］.北京:清华大学出版社，1998.