基于子带能量分布的图像自适应压缩采样方法

熊承义，程 赟，周 城

(中南民族大学电子信息工程学院，武汉430074)

在传统的信号或图像采集系统中，香农采样定理必须遵守的基本原则:要无失真地重建带宽有限的信号，其信号的采样频率必须大于或等于奈奎斯特采样率(信号带宽的两倍).依照香农采样定理会导致海量采样数据，这对处理时间和存储空间都是一种浪费.近年来，一种新兴的压缩感知(CS)［1-3］理论得到了研究人员的广泛关注.压缩感知是一种新的信号采集、编解码理论，能够实现数据采集和压缩同时进行.压缩感知理论认为，只要信号是稀疏或是可压缩的，那么它就能从一些少量的测量值中准确或近似重构.压缩感知理论的应用前景十分广阔，压缩感知应用于图像压缩成为当前的重要研究热点之一［3，4］.

在众多有关压缩感知理论的文献中［6-8］，大部分的测量矩阵都是预先设计好的，不需要根据测量信号而自适应变化.这种传统的CS方法，同等地对待信号的所有成分，并不考虑信号具有的先验特性.尽管对于大部分的现实信号，我们可能会并不预先知道信号的结构，然而对于大多复杂的图像信号，我们却知道这些信号的一些特性，比如图像各频率成分的分布特征等［8］.因此，基于图像先验信息的图像压缩感知，对于提高压缩感知系统的性能具有重要作用.利用人眼对图像低频成分敏感而对高频细节相对不敏感的视觉特性，在图像采集端对图像的不同频率成分分量进行不同自适应加权测量，对于降低采样比率和提高重建图像质量是一种有效方法［9］.本文在分析了图像分块离散余弦变换各子带能量分布特征的基础上，提出了一种新的基于子带能量分布的自适应加权图像压缩采样方法用于图像压缩应用.该方法通过提取各系数子带的能量用于图像在变换域的自适应加权测量，能够有效增强测量效率和提高重建图像质量.

1 基于分块的图像压缩感知

1.1 压缩感知

压缩感知主要包括两个环节:随机投影和非线性重构.图像压缩感知主要是对自然图像信号进行随机投影采样，并利用图像表示的稀疏性(sparse)作为先验知识进行优化重构.一个长度为N的一维离散时间信号x∈RN，可以表示为一组标准正交基的线性组合:

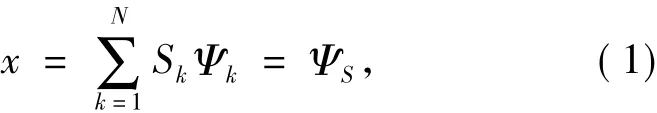
式中s与x是N×1矢量，Ψ是N×N矩阵.当信号x在某个基Ψ上仅有k≪N个非零系数时，称Ψ为信号x的稀疏基.信号的可稀疏表示是压缩感知的先验条件.常见的自然信号在时域内几乎都是不稀疏的，但是它们能够在某些变换域Ψ稀疏表示 .选择合理的稀疏基Ψ，可使得信号在该域具有良好的稀疏性 .常用的稀疏基有:正(余)弦基、小波基、chirplet基以及curvelet基等 .

在CS编码测量模型中，一般并不是直接测量可稀疏信号x本身，而是将信号x投影到测量矩阵上，从而得到信号的测量投影值y.测量过程可以表示为:

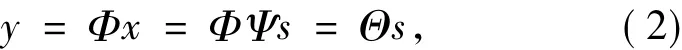
式中Φ为M×N测量矩阵，Θ=ΦΨ也称为M×N传感矩阵.通常由于M远小于N，所以，信号的压缩感知采样的维数将远小于信号传统奈奎斯特采样的维数.

如果由信号的压缩感知测量值矢量y重建原信号x，由于测量值矢量的维数M远远小于原信号的维数N，即方程的个数少于未知数的个数，这是一个欠定问题，一般来讲无确定解.然而由于式(2)中s是k稀疏的，当传感矩阵Θ满足有限等距性条件(RIP)时可以保证长度为N的x可以通过M≥O(klnN)个测量值准确重构.

RIP等价条件是测量矩阵Φ和稀疏表示的基Ψ不相干(Incoherence).Φ很大程度上和随机(Randomness)这个词相联系，CS信号的测量过程是非自适应的，测量矩阵的设计不依赖于信号的结构.目前，用于压缩感知的测量矩阵主要有以下几种［10，11］:高斯随机矩阵，二值随机矩阵(伯努力矩阵)，傅立叶随机矩阵，哈达玛矩阵，一致球矩阵等 .特别地，当Φ是高斯随机矩阵时，传感矩阵Θ能以较大概率满足约束等距性条件.高斯测量矩阵的优点在于它几乎与任意稀疏基都不相干，因而所需的测量维数将最小.

1.2 基于分块的压缩感知

由于现有CS方法在针对大尺度整幅图像采样时具有计算复杂度高，存储压缩采样算子所需存储器规模大的问题，采用基于分块的压缩采样方法能够实现较好的性能折衷［12］.分块CS的图像重构算法采用相同的采样算子以分块的方式获取图像.算法的基本思想是，首先将N=nr×nc个像素的图像x分成大小为B×B的块，第i个块的向量记为xi，i=1，…，n，n=N/B2;然后对每个块应用相同的压缩采样算子，得到每个图像块的测量值向量 .对每一分块图像的测量过程可表示为yi=ΘB xi，以及对整幅图像进行测量的等价测量算子可表示为由ΦB构成的对角矩阵［12］.

2 基于子带能量分布的压缩感知

2.1 变换域加权压缩采样

从上一节关于压缩感知的简介可知，传统压缩感知的测量过程是一个非自适应线性测量过程，其测量矩阵的设计不依赖于信号的结构.文献［9］提出一种在图像分块压缩采样阶段实行加权采样的方法，引入在对每个图像块保持测量维数相同的条件下，采用对被测量图像块在其变换域进行系数预加权后再进行压缩采样的技术.其测量效率将优于在解码端重加权重构技术［9］，该采样方法还可以有效降低解码端的复杂度.

这种加权采样方法通过利用图像统计特性在图像变换域修改采样权重，得到图像自适应的测量结果，能够达到有效降低系统采样比率的目的.其具体实现思想简述如下:

(1)修改图像编码端的压缩采样过程为:

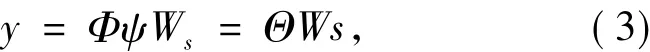
式中的矩阵W=diag［ω1，ω1，…，ωN］为测量加权矩阵，目的在于在实施压缩测量之前先将被测量变换域系数矢量进行加权处理，使得不同系数在最终生成的测量值中具有不同的信息量.

(2)修改图像解码端的重构过程为:

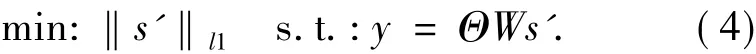
文献［9］选取对不同频率成分加权的权系数为对应频率成分的均值的绝对值|μi|及其均方差σi的线性组合，即:

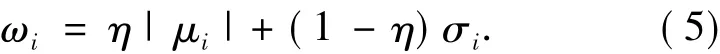
2.2 基于子带能量分布进行自适应加权测量

由于人眼对于图像信号不同的频率成分有不同的敏感度［6］，以及人眼类似于一个低通滤波器，对于低频成分更加敏感，根据人眼的视觉感知特性优化压缩采样过程，对于提高压缩采样效率应具有重要意义.基于人眼视觉特性的压缩采样，要求对直流和低频分量进行较大值的加权采样，而对高频分量进行较小值的加权采样，从而使得每一个压缩采样值提升直流和低频信息而相对抑制对应的高频信息.我们知道，对于自然图像的离散余弦变换(DCT)系数，大量值的频率部分集中在低频部分，该部分集中了图像信号的大部分能量，而高频部分量值较小，它仅占有图像信号的极少部分能量.基于以上分析和实验观察，本文提出了一种基于DCT域子带能量分布进行自适应加权测量方法.比较基于文献［9］的方法，本文方法不仅能够有效降低计算复杂度，而且能够更好地增强测量效率，提高重建图像质量.由于本文方法的测量过程与文献［9］方法的测量过程相同，主要区别在于采用新的基于图像能量分布的加权矩阵替代原来的基于统计特性的加权矩阵，因此主要给出新的加权系数矩阵的确定方法如下.

首先，提取每个分块图像DCT域对应相同位置的系数组成新的系数矩阵，得到代表图像在DCT域的不同系数子带.接下来，计算每个系数子带的能量.定义每个系数子带的能量为该子带内每个系数值的平方和 .具体来说，假设一幅nr×nc自然图像被分成B×B的块，那么它在DCT域可产生一共B×B个系数子带，则每个系数子带的能量将定义为:

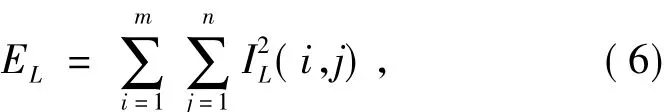
图1是256×256Lenna图经过8×8分块DCT，并经由Zigzag扫描后得到对应由低频到高频的64个子带的能量分布曲线图.图中的横坐标代表对应不同频率的系数子带，纵坐标代表子带的能量定义.从图1可直观看出:图像在DCT域的能量主要集中在直流和较少的低频分量;图像的高频分量占有很少的能量，通常频率越高占有的能量越少.

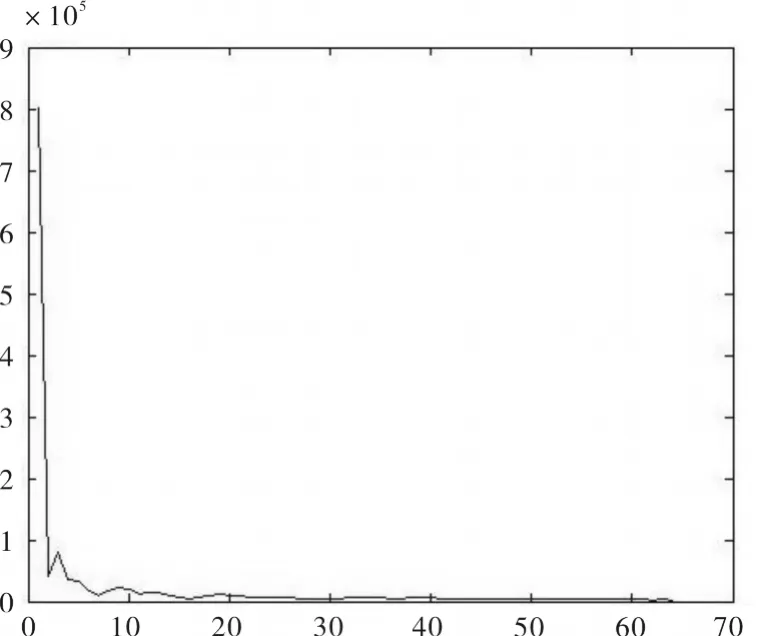
图1 子带能量分布曲线图Fig.1 Sub-band energy distribution curve

由此，我们最终提出直接采用各子带系数的能量比率作为相应的加权权重，在DCT域对相应频率系数进行加权后再进行压缩测量，即确定加权矩阵系数的选取原则为:

为了便于理解，定义改进的权重系数为相应子带能量的归一化结果，即:

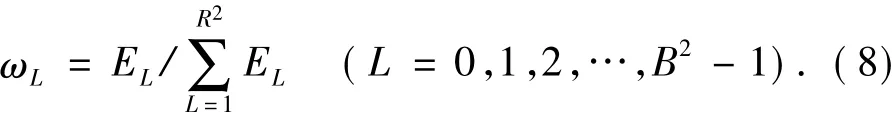
3 实验结果及分析

我们将基于本文提出的加权采样方法和文献［9］方法进行了比较.在实验中，采用高斯矩阵作为测量矩阵，采用nesta算法为恢复算法.为了充分地对比两种方法的性能，这里我们采用两组测试图像，一组是 256×256的灰度图像 lenna.bmp，cameramar.bmp，boat.bmp，另一组是 512 × 512 的灰度图像 lenna.bmp，house.bmp，manhatan.bmp .图像分块大小分别选择8×8和16×16.

表1是256×256的标准灰度图在各采样比率SR=0.2，0.3，0.4，0.5 下两种方法的 PSNR 性能比较结果，设置图像分块大小为8×8.表2是的512×512 标准灰度图在各采样比率 SR=0.2，0.3，0.4，0.5下两种方法的 PSNR性能比较结果，设置图像块大小为16×16.实验结果证明，采用本文方法可以提高PSNR性能平均在0.7dB及以上 .

图2给出了采样比率为0.4时的lenna.bmp和cameraman.bmp的重建图像的主观视觉效果比较 .图3所示为重建lenna图像的局部放大结果比较.可以看出，在相同的采样率下，采用本文提出的方法可更好地保留图像的重要细节信息，以及具有较少的重建噪声，因此具有更好的重建图像视觉质量.

表1 PSNR性能比Tab.1 PSNR PerformancedB

表2 PSNR性能比Tab.2 PSNR PerformancedB

图2 重建图像质量比较(SR=0.4)Fig.2 Visual quality comparison at sample rate 0.4 with block size 8 ×8

图3 Lenna重建图像的局部放大效果Fig.3 Locally zoomed parts of the reconstructed images

4 结语

基于自然图像在变换域各子带能量分布规律与人眼视觉感知一致性的特点，提出了一种基于子带能量分布的自适应加权压缩采样方法.大量实验结果表明:与同类方法比较，该方法不仅能够有效降低系统的计算复杂度，而且能够更好地降低测量比率和有效提高图像的重建质量.该压缩采样方法对基于新的压缩感知的图像压缩系统的设计具有较好的应用前景.另外值得注意的是，如果结合采用混合压缩感知技术［2］将会获得更佳的系统性能增益 .

［1］Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory ，2006，52(4):1289-1306.

［2］Tsaig Y，Donoho D.Extensions of compressed sensing［J］.Signal Processing，2006，86(3):533-548.

［3］Kumar A A，Makur A.Lossy compression of encrypted image by compressive sensing technique［C］//ICT.Proc Int Conf TENCON.Singapore:ICT，2009:1-5.

［4］Deng C ，Lin W，Lee B-S，et al.Robust image compression based on compressive sensing［C］//IEEE.2010 International Conference on Mulimedia and Expo.Singapore:IEEE ，2010:462-467.

［5］Ji Shi-hao，Xue Ya，Carin L.Bayesiancompressivesensing［J］.IEEETransactiononSignal Processing，2008，56(6):2346-2356.

［6］李 林，孔令富，练秋生.基于轮廓波维纳滤波的图像压缩传感重构［J］.仪器仪表学报，2009，30(10):2051-2056.

［7］练秋生，高彦彦，陈淑贞.基于两步迭代收缩法和复数小波的压缩传感图像重构［J］.仪器仪表学报，2009，30(7):1426-1431.

［8］Yang Yi，AU Oscar C，Fang Lu ，et al.Preceptual compreesive sensing for image signals［C］//IEEE .2009 International Conference on Multimedia and Expo.New York:IEEE，2009:89-82.

［9］Yang Yi，AU Oscar C，Fang Lu，et al.Reweighted compressive sampling for image compression［C］//PCS.2009 Picture Coding Symposium，Chicago:PCS，2009:1-4.

［10］Candes E J ，Tao T.Near optimal signal recovery from random projections:universal encoding strategies［J］.IEEE Transactions on Information Theory，2006，52(12):5406-5425.

［11］Jing Zou，Gilbert A C，Straussm J，etal.Theoretical and experimental analysis of a randomized algorithm for sparse Fourier transform analysis［J］.Journal of Computational Physics，2006，211(2):572-595.

［12］Gan L.Block compressed sensing of natural images［C］//DSP.2007 15th International Conference on Digital Signal Processing， Cardiff:DSP，2007:403-406.