Radon不等式的等价形式及其应用

●李群芳 赵焕光 (温州大学数学与信息科学学院 浙江温州 325035)

Radon不等式的等价形式及其应用

●李群芳 赵焕光 (温州大学数学与信息科学学院 浙江温州 325035)

Radon不等式［1］也称权方不等式，是由捷克籍奥地利数学家Jahann Radon在1952年首先建立的．实际上，Radon不等式就是著名的Hölder不等式［2］的一种等价形式，该不等式在不等式证明中有着广泛的应用．本文第一部分利用凸函数f(x)=x1+m(其中m＞0)的Jensen不等式［2］给出3种应用非常方便的Radon不等式的等价形式，并通过举例说明它们在分式无理不等式证明中的巧妙应用;第二部分利用Radon不等式证明一个能统一许多不等式的权方和不等式．

1 Radon不等式的等价形式

命题 1若 ai＞0，bi＞0(i=1，2，…，n)，m ＞0，则下述不等式成立:

2 Radon不等式在分式无理不等式证明中的应用

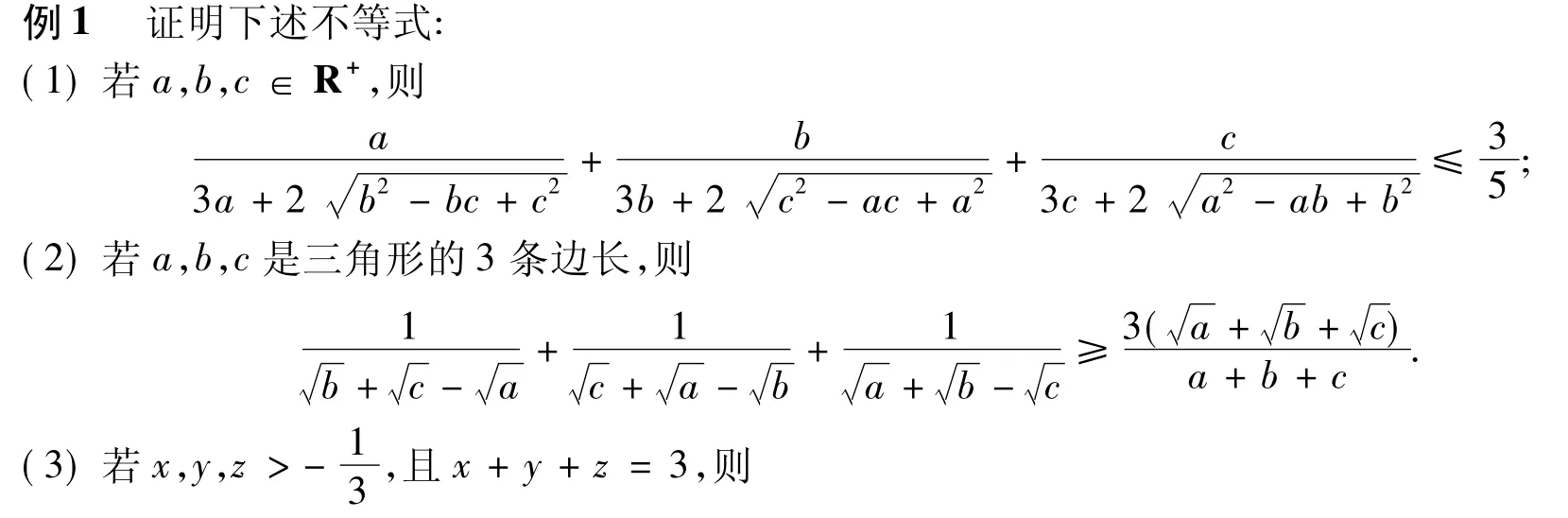
注在文献［3］中，利用切线方程证明了例3的(1)，(2)，(3)，其过程非常复杂．从上述证题过程可以看出，运用Radon不等式证明分式无理不等式具有一定的优越性．

3 利用Radon不等式证明权方和平均不等式

注显然，文献［4］的主要结果定理1是权方和平均不等式的特例，文献［5］与文献［6］的部分结果也是权方和不等式的特例．

下面再举例说明权方和不等式的其他应用．

［1］ 刘培杰．数学奥林匹克试题背景研究［M］．上海:上海教育出版社，2006．

［2］ 匡继昌．常用不等式［M］．济南:山东科学技术出版社，2004．

［3］ 张宏．利用切线方程证明不等式［J］．中等数学，2009(4):6－12．

［4］ 季明银．一类不等式的推广［J］．数学通报，2008(1):60－61．

［5］ 罗邦华．问题1624的别证及推广［J］．数学通报，2008(5):50．

［6］ 钟建新．问题1748的推广及应用［J］．数学通报，2009(4):45－46．