基于自适应径向基函数的整车耐撞性多目标优化
2011-02-01陈国栋刘桂萍赵子衡
陈国栋 韩 旭 刘桂萍 赵子衡
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
基于自适应径向基函数的整车耐撞性多目标优化
陈国栋 韩 旭 刘桂萍 赵子衡
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
提出自适应径向基函数代理模型,并结合微型多目标遗传算法对整车耐撞性进行优化。在每个迭代步中,以最优拉丁方进行样本点设计,以遗传最优拉丁方进行测试点设计,通过隔代映射遗传算法对径向基函数代理模型的误差进行评价并获得最优光滑参数。将测试点不断添加到样本空间,直至耐撞性各个目标代理模型在测试点的误差都达到要求,再采用贪婪算法将最后迭代步的测试点筛选到样本空间以进一步提高精度。最后采用微型多目标遗传算法对达到许可误差的各个自适应径向基函数模型进行优化,获得Pareto前沿面,根据工程要求或工程人员的经验权衡耐撞性,优化各个目标之间的关系以获得不同最优妥协解。
自适应径向基函数;光滑参数;多目标优化;整车耐撞性
0 引言
在汽车耐撞性优化过程中存在如下问题:目标和约束不能显式表达,单次模拟时间长。为解决以上问题,响应面(RSM)[1]、逐步回归模型[2]、移动最小二乘[3-4]、K riging模型[5]等代理模型已被广泛地应用于汽车结构耐撞性优化中。碰撞是个涉及非线性的复杂瞬态动力学过程,设计变量与某些目标或约束(如加速度峰值)之间非线性程度高,而响应面法对非线性拟合能力不足。逐步回归模型只是以减少不必要的多项式项来减少最小样本点个数[2]。移动最小二乘法在局部进行拟合,对非线性问题的求解有很大改善,但需要样本点较多,同时精度在很大程度上取决于权系数[3]。K riging模型需要应用一个全局优化步骤来鉴定最大似然估计,较难构造和使用[6]。径向基函数(radialbasis function,RBF)作为一种有效的代理模型在国内还没有用于整车汽车耐撞性优化的实例。Fang等[7]成功地将RBF用于道奇士整车碰撞优化中,与RSM法进行比较,RBF更稳定可靠。Jin等[8]利用14个代表不同类型问题的算例,对常见4种代理模型进行了系统比较,发现在同时考虑模型精度和鲁棒性的情况下,RBF最为可靠。但RBF存在两个缺陷制约着它的广泛使用:①RBF存在对模型精度影响很大的光滑参数,但缺乏获得最优光滑参数的方法。通常光滑参数的选择凭借使用者的经验[7,9]。实际上针对不同的问题,不同的样本,最优光滑参数不同[10]。国外一些文献采用交叉验证方法(CV)来获得光滑参数,但Jay等[11]发现这种方法不稳定,可能导致模型精度很差。②RBF缺乏合适的模型验证和更新的方法。RBF通过插值来构造,不能像响应面拟合那样,通过样本点误差来评价整个模型的误差。额外随机挑选测试点,随机性太大,而且测试点的获得耗费额外的费用。CV方法不能真实地评价模型的精度[6]。
汽车耐撞性优化是个要同时考虑耐撞性和轻量化的多目标优化问题[3]。耐撞性和轻量化目标之间相互冲突,不存在同时达到最优的解。张勇等[4]通过对耐撞性的约束将优化目标转化到轻量化一个目标上;张宏波等[3]通过博弈中的纳什均衡平衡耐撞性和轻量化的冲突,以纳什均衡状态作为最优解;孙光永等[12]通过最小距离选解法权衡各个目标以获得最优解。线性加权法在优化前必须给定各个目标的权系数,主观性太大。主要目标法必须确定目标转化为约束的对象和约束的大小。博弈方法克服了线性加权法依赖于权系数的缺点,但通常不满足Pareto最优条件[3]。上面的方法都是将多目标问题通过各种策略转化到只获得一个解,即获得一个方案。
考虑到光滑参数对RBF的影响以及缺乏模型验证和更新的方法,笔者提出自适应径向基函数方法。它通过获得最优光滑参数最大化模型的精度,并对模型精度系统作评价,更新模型直到达到规定的误差范围。而微型多目标遗传算法采用少量个体数来提高效率,采用重启动策略和探测算子保证Pareto的全局性,在大量工程算例中得到了应用[13]。本文结合自适应径向基函数和微型多目标遗传算法求解整车耐撞性优化问题,寻找到Pareto前沿面,根据工程人员的经验权衡耐撞性和轻量化之间的关系来获得不同的最优方案。
1 自适应径向基函数
1.1 径向基函数
构建代理模型首先需要对优化变量搜索空间进行采样。样本点选择不当易导致代理模型精度较低甚至难以构造,试验设计(design of experim ents,DOE)的理论可帮助确定合理的样本点。本文采用最优拉丁方试验设计(optimal latin hypercube design,OLHD)[14]获得样本点,使样本点在整个设计空间均匀分布。最优拉丁方试验设计具有效率高,均衡性能好的优点。
径向基函数[7-8]是以径向函数为基函数通过线性叠加构造的模型。对于某一实际模型 f(x),其RBF代理模型~f(x)可表示如下:
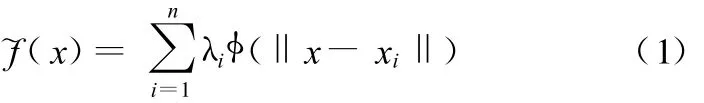
式中,n为样本点个数;‖x-xi‖是待测点x与第i个样本点xi之间的欧氏距离;φ为基函数;λi为要求解的权系数。
根据n个样本点插值条件,可以得到方程组:

其中,aij为矩阵A中的元素。
常用基函数及光滑参数如表1所示,在相同试验设计情况下,Fang等[7]对各种基函数进行比较,发现采用MQ基精度最高,此处我们也选用MQ基。

表1 常用基函数及其光滑参数[7-8]
式(2)表明,对于一组样本点,矩阵A决定权系数λ,也即决定代理模型的构造。而光滑参数决定着矩阵A,光滑参数越大,每个样本点产生的影响域越大,构造的模型越平滑,代理模型通常越精确,但矩阵A的条件数急剧增加,可能造成模型精度突然急剧降低。RBF经过每个样本点,而样本点之间的构造形式受光滑参数的影响,图1所示为不同光滑参数在相同样本下构造的RBF模型,其中,x表示设计变量,f表示关于x的响应。
代理模型构造完后必须验证模型的精度,RBF是一种插值模型,样本点处误差为零,不能像多项式拟合那样通过样本点误差来评价整个代理模型的误差。必须通过额外的测试点来评价,通常用平均相对误差(APE)、决定性系数(R2)来评价:

图1 不同光滑参数在相同样本下构造的RBF模型

额外的测试点的个数和位置具有很大的偶然性和随机性。
1.2 遗传最优拉丁方试验设计
在代理模型误差未达要求情况下,遗传拉丁方试验设计[15](ILHD)可以遗传样本点产生修正点来更新代理模型,从而避免了在整个设计空间重新采样,造成样本点的浪费,提高了效率。但修正点添加到样本点中,不能保证在空间均匀分布,更新的代理模型会丢失局部信息。
本文结合OLHD和ILHD得到遗传最优拉丁方试验设计(inherited op timal latin hypercube design,IOLHD)方法,它采用模拟退火法以最大化最小距离准则遗传拉丁方获得修正点。
IOLHD具有以下两个特征:①修正点距离样本点的距离大;②修正点添加到样本点中,依然能保证在设计空间均匀分布。以二维设计空间为例,样本点的分布如图2所示,其中横坐标和纵坐标分别表示二维设计变量,图2a表示OLHD获得样本点的分布;图2b表示遗传图2a中样本点获得的修正点的分布;图2c表示合并的样本点和修正点的分布。合并后每个横竖格子里面只有一个样本,依然保持着拉丁方试验设计的特点。
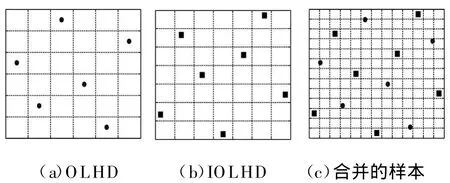
图2 试验设计
RBF的最优光滑参数很难确定,但在一个大概确定的范围内。根据RBF模型的插值特点,距离样本点越近,误差越小,直至样本点处误差为零,距离样本点越远处误差可能越大。根据IOLHD采样特征①,采用模拟退火法以最大化最小距离准则来获得修正点,所获修正点离样本点的距离是最大的。于是以OLHD产生的样本点构造RBF,以IOLHD产生的修正点作为测试点。因为测试点距离样本点距离最大,误差可能最大,于是以测试点的误差最小为目标在光滑参数的区间内确定最优光滑参数。根据IOLHD遗传采样的特征②,样本点和修正点(即测试点)构成的样本点集在整个设计空间里面还是均匀分布的。所以当确定了最优光滑参数后,若测试点误差没有处于设定的模型误差范围内,就将测试点添加到样本点中去,重新获得测试点和合适的光滑参数,直至测试点误差达到设定的模型误差范围。
1.3 隔代映射遗传算法
为了提高搜索最优光滑参数的效率,在每次迭代中,以光滑参数为设计变量,以样本点构造的RBF模型计算的测试点误差为适应度,采用隔代映射遗传算法[16](IP-GA)作为搜索工具。IPGA在小种群遗传算法(μGA)的基础上添加了隔代映射算子,通过父代和祖代的最优个体的变化方向来搜寻更好的个体,这样通过它在父代和祖代的最优个体附近的搜索,大大增强了算法的局部搜索能力,提高了收敛效率。达到全局最优点时所用的代数仅仅是μGA的6.4%~74.4%[17]。
1.4 贪婪算法
在模型误差达到要求、同时确定了当前样本点下的最优光滑参数后,面临的一个问题是怎么处理最后一个迭代中产生的测试点。由于最优光滑参数是在当前样本情况下确定的,样本点改变,最优光滑参数一般也会改变,若将最后迭代产生的测试点全部加入到样本中去,虽然样本点增多但不是在最优光滑参数下构造RBF,模型精度很可能会降低。若都不加入到样本中去,只会保证是在最优光滑参数下构造RBF,而没有充分利用最后迭代步的测试点,特别是在测试点耗费大量计算机资源的时候。
本文通过贪婪算法[17]挑选出部分最后迭代步的测试点添加到样本空间中,最大限度地利用试验样本来提高模型精度。
2 微型多目标遗传算法
微型多目标遗传算法(micro multi-objec-tive genetic algorithm,μMOGA)[13]采用小规模进化种群,一般为5~8个(常见MOGA种群大小为20~100个),可以减少目标值的计算次数,提高优化效率。采用重启动策略和个体拥挤距离比较方法保持进化种群中个体基因和外部种群多样性。为了加快收敛速度,在重启动时加入了一种探测算子,在非支配解分布密集和分布稀疏区域各产生一个新个体,对非支配解的区域进行探测性的局部搜索。通过与大量测试函数[13]比较发现,μMOGA与NSGAⅡ等常见多目标遗传算法相比,在收敛速度和非支配解分布均匀度上具有明显的提高。
3 基于自适应径向基函数的耐撞性多目标优化方法
运用自适应径向基函数构造碰撞各个目标和约束的代理模型。通过自适应得到最优光滑参数,从而可以最大化模型的精度,减少碰撞有限元模型的计算次数;对模型精度进行系统的评价并更新模型达到许可误差。再运用高效率微型多目标遗传算法获得Pareto前沿面。整个优化过程的流程如图3所示,其基本步骤如下:

图3 基于ARBF的整车耐撞性多目标优化流程图
(1)确定耐撞性的各个目标和约束,选择对目标影响大的部件为设计变量。
(2)初始化,给定光滑参数R和q、每个目标和约束的误差范围、样本点个数n s、测试点个数n t。
(3)采用OLHD试验设计获得n s个样本点,并代入实际有限元模型中,计算目标值和约束值。
(4)采用步骤(3)中n s个样本点获得n t个测试点,代入实际有限元模型中,计算目标值和约束值。
(5)以光滑参数为设计变量,以ns个样本点构造的RBF模型计算的n t个测试点误差为适应度,采用IP-GA获得最优光滑参数。
(6)计算步骤(5)中得到的最优光滑参数对应的测试点误差。若大于设定的误差范围,更新样本n s←n s∪n t,再转步骤(4);否则转步骤(7)。
(7)通过贪婪算法挑选出最后迭代步中部分测试点,添加到样本中。
(8)运用μMOGA对通过贪婪算法确定的最终样本点和步骤(5)中获得的最优光滑参数构造的自适应径向基函数(adap tive radial basis function,ARBF)模型进行优化。
(9)输出Pareto前沿面,根据实际工程人员的设计要求和偏好从Pareto前沿面中选择最优妥协解。
4 某车型整车耐撞性多目标优化
4.1 有限元模型的建立
图4给出了早期开发阶段某车型整车正面碰撞有限元模型。某车以50km/h速度撞向固定刚性墙,整个过程的数值仿真时间为150ms,数值仿真采用有限元软件LS-DYNA。
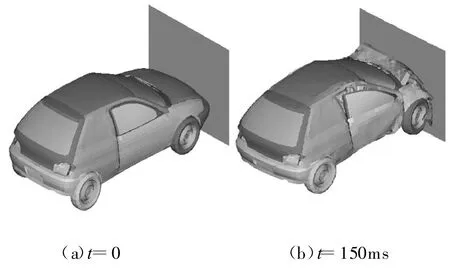
图4 某车型正面碰撞有限元模型
4.2 多目标优化问题的建立
在汽车的正面碰撞车体,冲击加速度峰值最大,乘员头部、胸部伤害较严重,选择B柱加速度峰值最小作为一个目标;为了保证乘员有足够的生存空间,选择脚踏板侵入量为另一个目标;轻量化是永恒的主题,整车质量最小为第三个目标。这些目标之间相互冲突,不存在同时达到最优的解。
国内外的研究表明,在正碰时车辆前部结构吸收的能量占车辆总吸收能量的50%以上[12]。前部结构的吸能特性和变形模式决定着车身在撞击时的加速度或力的响应。图5为从整个模型222个部件中选择的10个主要吸能前部结构部件图。如图6所示,在第20m s时吸收的能量占总吸收能量的53%,在第150ms时吸收的能量占总吸收能量的45%。选择这10个部件为设计变量,其中3个部件左右对称,于是共有7个设计变量。

图5 设计变量部件
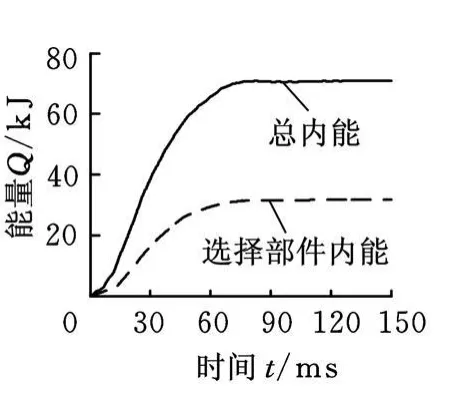
图6 随时间历程的内能变化

4.3 优化结果及分析
选用MQ形式基函数,设定光滑参数范围0≤R≤2,0<q≤3。选择初始样本点n s和每个迭代步测试点n t都为10个。板厚与车体质量m之间基本呈线性关系,选择m的许可误差ε3≤1%;而板厚与B柱加速度峰值a之间非线性度高,伴随着波动和噪声,误差很难收敛到很小,选择a的许可误差ε1≤6%;脚踏板侵入量d的许可误差ε2≤6%。
图7所示为第一个迭代步中光滑参数对d的影响曲面。在第一个迭代步中,在样本点相同的情况下,脚踏板侵入量 d的代理模型误差范围为6.2%~46%,可见光滑参数对模型精度影响很大。各个代理模型在不同样本情况下,最优光滑参数随迭代步的变化如图8所示。

图7 第一个迭代步中光滑参数对d的影响
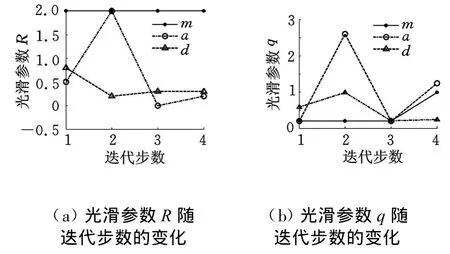
图8 各代理模型最优光滑参数随迭代步的变化
构造ARBF的迭代过程如图9所示,共迭代4次,a、d和m 的误差分别达到5.71%、3.72%和0.1%,都达到了各自的许可误差。

图9 各个目标代理模型误差随迭代步的变化
采用μMOGA对3个ARBF模型进行优化,输出100个Pareto解,如图 10所示。
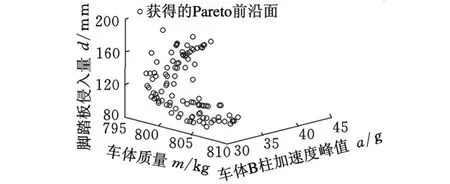
图10 获得的多目标Pareto前沿面
根据工程要求或工程人员的经验权衡耐撞性和轻量化之间的关系,选择Pareto前沿面中的某个解为设计方案。优化前后各代理模型最优光滑参数比较如图11~图13所示。若着重提高安全性能,可选择方案一,此时B柱加速度峰值降低25.7%,脚踏板侵入量减少36.5%,质量仅增加6.8kg;若同时考虑安全性和轻量化,可选择方案二,B柱加速度峰值降低18%,脚踏板侵入量减少3.5%,质量也减轻1kg。
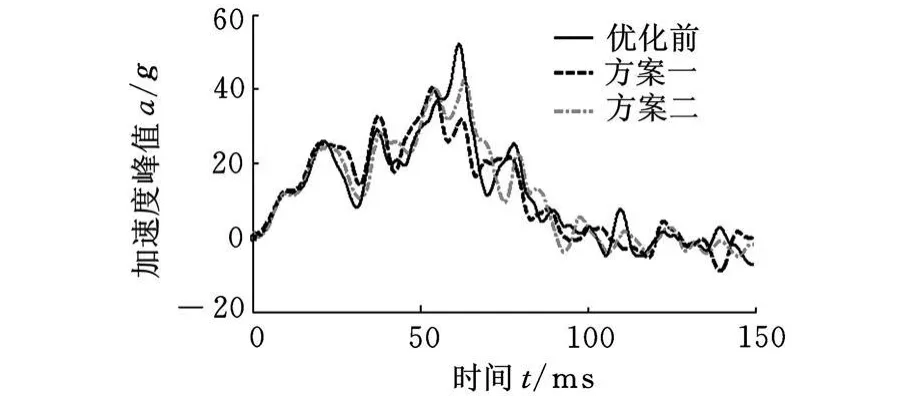
图11 优化前后B柱加速度曲线

图12 优化前后质量

图13 优化前后脚踏板侵入量
5 结束语
将具有较强非线性描述能力的径向基函数应用到汽车碰撞中,考虑到径向基函数精度受光滑参数影响和缺乏系统的模型验证、更新方法等缺点,提出自适应径向基函数。它通过获得最优光滑参数来最大化碰撞各个目标代理模型的精度,减少有限元模型的调用次数。对代理模型精度系统进行了评价,并进行了代理模型迭代更新,构造了满足碰撞各个代理模型精度要求的模型。结合了自适应径向基函数和微型多目标遗传算法,对某整车正碰中10个主要吸能部件的板厚分布对整车耐撞性和轻量化的影响进行了优化,获得了多目标Pareto前沿面,根据工程要求或工程人员的经验权衡耐撞性和轻量化之间的关系,从Pareto前沿面中挑选出了不同的最优妥协方案。
[1] 王海亮.基于耐撞性数值仿真的汽车车身结构优化设计研究[D].上海:上海交通大学,2002.
[2] 张维刚,廖兴涛,钟志华.基于逐步回归模型的汽车碰撞安全性多目标优化[J].机械工程学报,2007,43(8):142-147.
[3] 张宏波,顾镭,徐有忠.基于博弈论的汽车耐撞性多目标优化设计[J].汽车工程,2008,30(7):553-556.
[4] 张勇,李光耀,钟志华.基于移动最小二乘响应面方法的整车轻量化设计优化[J].机械工程学报,2006,42(6):1-6.
[5] Forsberg J,N ilsson L.On Polynom ial Response Surfaces and K riging for Use in Structural Optim ization of Crashworthiness[J].Struct.Multidisc.Optim.,2005,29:232-143.
[6] Wang G G,Shan S.Review of M etamodeling Techniques in Support of Engineering Design Optim ization[J].Journal o f Mechanical Design,2007,129(371):370-380.
[7] Fang H,Rais-Rohani M,Liu Z,et al.A Comparative Study o fMetamodeling Methods forMu ltiob jective Crashworthiness Optimization[J].Computers&Structures,2005,83:2121-2136.
[8] Jin R,Chen W,Simpon TW.Comparative Studies o f Metamodelling Techniques under Multip le Modeling Criteria[J].Struct.M ultidisc.Optim.,2001,23:1-13.
[9] Wang JG,Liu G R.On the Optimal Shape Parameters of Radial Basis Function Used for 2-D M eshless Method[J].Comput.Methods App l.Mech.Engry.,2002,191:2611-2630.
[10] Shmuel R.An A lgorithm for Selecting aGood Value for the Parameterc in Radial Basis Function Interpolation[J].Advances in Computational Mathematics,1999,11(2/3):193-210.
[11] Martin JD,Simpson T W,Use of K riging M odels to App roximate Deterministic Com puter M odels[J].A IAA Journal,2005,43(4):853-863.
[12] 孙光永,李光耀,钟志华,等.基于序列响应面法的汽车结构耐撞性多目标粒子群优化设计[J].机械工程学报,2009,45(2):224-230.
[13] 刘桂萍.基于微型遗传算法的多目标优化方法及其应用[D].长沙:湖南大学,2008.
[14] MorrisM D,M itchell T J.Exp loratory Designs for Computational Experiments[J].Journal of Statistical Planning and Inference,1995,43(3):381-402.
[15] W ang G G.Adap tive Response Surface Method Using Inherited Latin Hypercube Design Points[J].J.Mech.Des.,2003,125:210-220.
[16] Liu G R,H an X.Computational Inverse Techniques in Nondestructive Evaluation[M].Florida:CRC Press,2003.
[17] 黄永辉.基于实时计算方法的结构动力学快速分析方法及其应用研究[D].长沙:湖南大学,2008.
Multi-objective Design Optim ization on Crashworthinessof Full Vehicle Based on Adap tive Radia l Basis Function
Chen Guodong Han Xu Liu Guiping Zhao Ziheng
State Key Laboratory of A dvanced Design and Manufacturing for Vehicle Body,H unan University,Changsha,410082
An ARBF model method was suggested and combined w ith micro m ulti-objective genetic algorithm(μMOGA)to solve vehicle crashworthiness.In each iterative,samp ling points were obtained by the optimal Latin hypercube design,while testing points were obtained by the inherit op timal Latin hypercube design,this method regarded the errors of testing points as fitness of intergeneration projection genetic algorithm(IP-GA),assessed themodel systematically and got the op timal sm ooth parameters to maximize model accuracy,testing points added to sam ple space until reaching errors allow able of each crashworthiness objective.Then greed algorithm was adopted to filter the testing points from the last iterative to sam pling space to increase accuracy.A t last,μMOGA was app lied to op timize the ARBF,and got Pareto and balanced each ob jective to get different best com p romise solutions according to engineer experim ents or engineerring requirements.
adap tive radial basis function(ARBF);smooth parameter;m ulti-objective op tim ization;vehicle crashworthiness
TP18;TG386
1004—132X(2011)04—0488—06
2010—04—20
国家自然科学基金资助项目(10725208);国家重点基础研究发展计划(973计划)资助项目(2010CB832700);高等学校博士学科点专项科研基金资助项目(200805321034);国家科技重大专项(2010ZX04017-013-005)
(编辑 王艳丽)
陈国栋,男,1983年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。主要研究方向为多目标优化算法、汽车车身结构CAE、汽车碰撞安全。韩 旭,男,1968年生。湖南大学机械与运载工程学院院长、教授、博士研究生导师。刘桂萍,女,1980年生。湖南大学机械与运载工程学院讲师。赵子衡,男,1983年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。
