基于模型和广义点摄影测量的圆柱体自动三维重建与检测

郑顺义，郭宝云，李彩林

1.武汉大学遥感信息工程学院，湖北武汉430079；2.湖北工业大学计算机学院，湖北武汉430068

圆柱是工业零件中基本的几何结构，大量的工业零件如轴承、滚柱、转轴、销等都是圆柱体的，同时圆柱也是更多复杂零件的基本组成部分。因此圆柱体的三维重建与检测是工业零件检测的重要内容之一。但是目前这方面的研究还较少，仅文献［1］基于物体成像轮廓对圆柱体进行了视觉测量与重建，引入圆柱体模型，讨论了基于模型重建的优势，取得较好的重建结果。但该算法要求圆柱轮廓（包括顶面圆、底面圆和母线）中顶面圆和底面圆上空间点与像点是对应点，但对于圆来说并不存在严格的对应点；另外其初始值需要手工给定。

共线方程［2］作为摄影测量的核心方程，已经广泛应用于摄影测量的各个领域，但是在传统的摄影测量理论中，共线方程的使用前提是要先提取出严格意义上的同名点，这在很多情况下比较难以实现。广义点摄影测量理论［3］，扩展了共线方程的使用范围，不再需要空间点与像点间严格的对应关系。这对于不能提取出严格意义上的同名点的一些工业零件来说，使用广义点摄影测量平差模型进行解算，可以达到很好的量测精度。文献［4］曾基于广义点摄影测量完成圆和圆角矩形的三维重建，文献［5］借助于广义点摄影测量理论完成钣金件上圆的检测，文献［6］也基于广义点摄影测量计算同心圆孔的物方参数，都取得了较好的结果。

本文在此基础上，结合边缘曲线编组的椭圆提取方法［7－11］，提出一种基于模型和广义点摄影测量理论的圆柱体自动三维重建与误差检测方法，推导出基于圆柱体几何模型的广义点平差模型，并且给出自动获取初始值的方法，从而直接解算出圆柱体的模型参数，实现圆柱体的自动三维重建与尺寸检测。

1 圆柱的数学模型与轮廓表达

以圆柱体底面圆的圆心O为原点，底面圆所在的平面为XOY面，形成的右手坐标系O－XYZ作为圆柱体的模型坐标系。如图1所示，在模型坐标系中，圆柱体有两个参数：圆柱的高H和半径R。

图1 圆柱体模型坐标系Fig.1 Model coordinate system of cylinder

圆柱体在影像上投影的轮廓为顶面圆、底面圆和圆柱的两条母线，通过图2可以确定这两条母线对应的角度为θ1和θ2，其中摄影中心S（XS，YS，ZS）在模型坐标系中坐标为S′（X′S，Y′S，Z′S），D点为S′在XOY面上的投影。DA和DB为D点到底面圆的两条切线。

图2 影像上两条可视母线对应的角度（θ1和θ2）分析［1，12］Fig.2 Analysis of angles（θ1andθ2）related to two visual generatrix of cylinder contours［1，12］

令

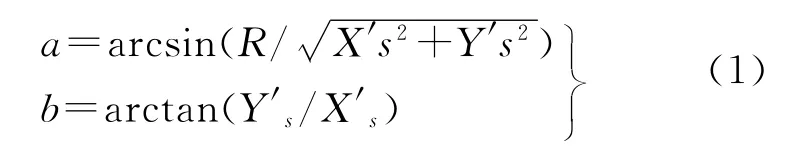
则

当Xs＞0时

当Xs＜0时

则轮廓中顶面圆和底面圆可通过式（4）来表达，两条母线利用式（5）计算得到。

2 基于广义点摄影测量的圆柱体数学平差模型

2.1 广义点摄影测量

传统摄测量中的“点”指的是“物理”意义上（或称为“可视”）的点，如圆点、交叉点、角点、端点等。在现实世界中除了物理点外还存在着大量的曲线，如河流、道路以及工业零件上的圆、圆弧和二次曲线等。在数学上，所有的直线和曲线都是由点构成的，与可视点一样，共线方程也可用到线特征中的点，而且摄影测量中的所有特征都可以归结为“点”，以适合共线方程，这就是所谓的广义点摄影测量［3］。广义点摄影测量是传统点摄影测量的扩充，与传统摄影测量又有本质的区别，即不再需要空间点与像点间严格的对应关系。其基本数学形式见下式。

广义点是“数学”意义上的点，包括直线上的点、曲线上的点，以及灭点等，这些点和物理意义上的点统称为广义点。根据“广义点”理论，曲线（或直线）上任意一个点都可以作为“控制点”，而且可以直接应用“共线方程”，其与物理意义上的点之间仅有的差别就在于：物理意义上的点使用关于x和y的两个共线方程，而特征线上的点根据线段的方向仅仅使用关于x或y的一个共线方程。当将特征线的参数方程代入共线方程时，可以通过平差的过程，同时解算出特征线的参数，从而直接求解出特征线。因此，点、直线、圆、圆弧、任意曲线很容易归纳为一个数模型——共线方程，进行统一平差。本文利用广义点摄影测量的这个优势，直接解算出圆柱体的各个空间参数。

2.2 基于模型和广义点摄影测量的圆柱体数学平差模型

空间中的圆柱体可以使用底面圆圆心（X0，Y0，Z0），半径R，中心轴线方向向量（Vx，Vy，Vz）和圆柱高度H唯一表示。利用圆柱体数学模型计算物方坐标系中圆柱体轮廓上点的空间坐标，需要建立圆柱体模型坐标系O－XYZ与物方坐标系O′－X′Y′Z′（检校中确定的坐标系）之间的关系。

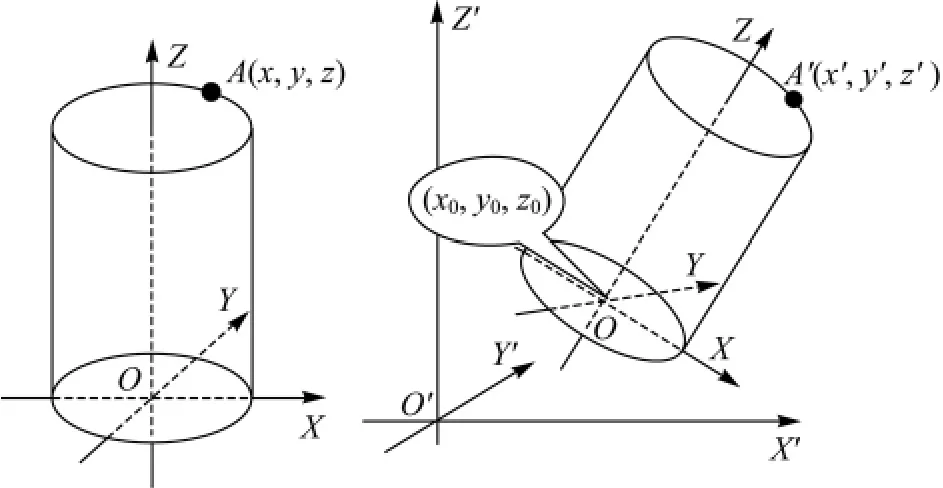
图3 圆柱体模型坐标系与物方坐标系的关系Fig.3 Relationship between cylinder model coordinate system and spatial coordinate system

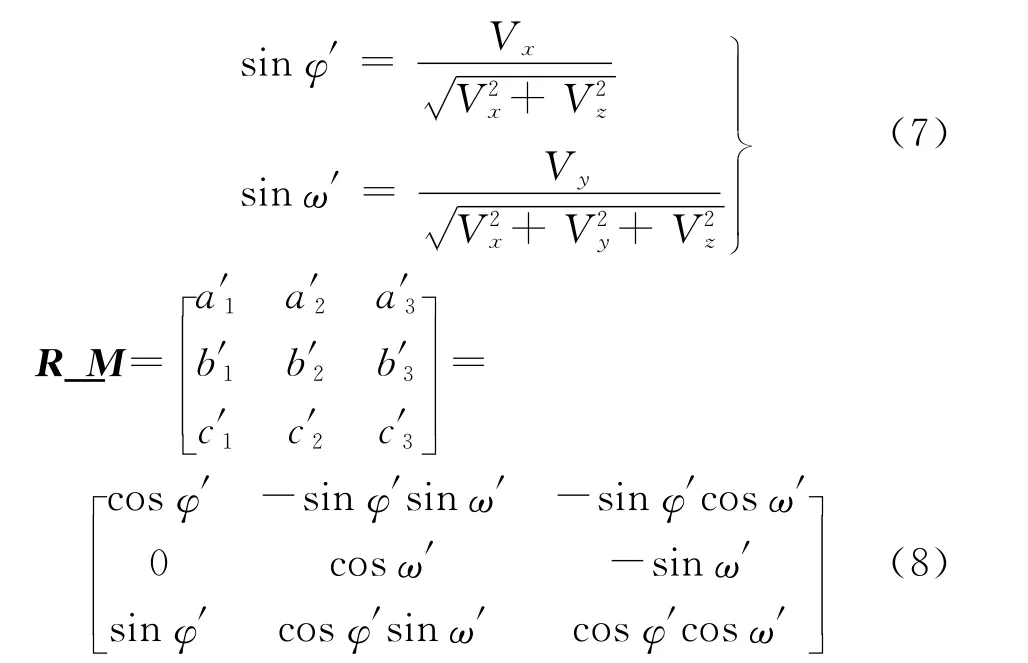
圆柱体轮廓线在模型坐标系中的坐标和物方坐标系中的坐标的转换关系见式（9）。其中A为模型坐标系中圆柱体轮廓上任意一点，A′为A在物方坐标系中对应点的坐标（见图3）。

将式（4）、式（5）计算出的圆柱体轮廓在模型坐标系中的坐标代入式（9），得到所有点在物方坐标系下的空间坐标（X′，Y′，Z′）。

将式（10）计算出的空间点坐标代入式（6）得到基于圆柱体几何模型的广义点摄影测量构像方程，如式（11）所示。

式中，（X0，Y0，Z0）为底面圆的圆心在物方坐标系中的空间坐标；R为半径；θ为顶面和底面圆轮廓离散采样的角度值，对于母线来说是θ对应于影像上可视母线的角度值；（Xs，Ys，Zs）是相机位置；（aj，bj，cj），j＝1，2，3为物方坐标系下相机参数的旋转矩阵；（a′j，b′j，c′j），j＝1，2，3为圆柱体模型坐标系与物方坐标系之间的旋转矩阵；f为相机的焦距；（xi，yi）为像点坐标；（x0，y0）为像主点坐标；（Δx，Δy）为畸变差改正值，计算公式见式（12），其中r2＝（x－x0）2＋（y－y0）2，K1、K2为径向畸变差，P1、P2为偏心畸变差。从式（11）可以看出，构像方程中圆柱体有7个参数：底面圆心坐标（X0，Y0，Z0），半径R，圆柱高度H，圆柱模型坐标系与物方坐标系之间的两个旋转角φ′、ω′。

如图4所示，点p为圆柱的底面或顶面圆上任意一点在像方投影，其构像方程根据p点处的切向量方向角α来确定。

图4 圆柱轮廓中圆的广义点摄影测量模型Fig.4 Generalized point photogrammetry model of circles in cylinder contours

母线上每个点的构像方程通过该母线在影像上投影的直线的方向来确定。

将式（11）线性化，得到基于圆柱体几何模型和广义点摄影测量的数学平差模型，见下式

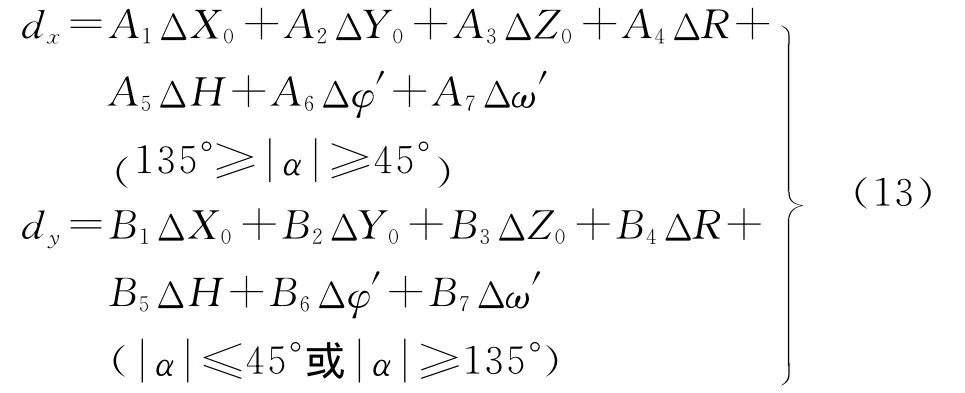
式中，A1、A2、A3、A4、A5、A6、A7和B1、B2、B3、B4、B5、B6、B7为改正数系数；dx、dy为常数项。

式中，x、y为圆柱体投影到影像上的轮廓点的坐标；x′、y′为影像上的相应的真实轮廓点的坐标。

3 圆柱体重建流程

在建立了圆柱体的几何模型以及平差模型后，对圆柱体进行三维重建，重建步骤主要包括初始值计算、广义点迭代平差两个方面，流程图如图5所示。

3.1 初始值计算

（1）利用canny算子对已标定的立体相机拍摄的两幅影像分别进行边缘提取，然后对提取的边缘进行细化、跟踪，去除短边缘，得到曲线段集合［13－14］。

（2）根据曲率在曲线段集合中识别影像中圆柱体上下椭圆部分，利用边缘曲线编组的椭圆提取方法分别拟合上下椭圆［7－11］。这是保证初始值正确获取的关键。

（3）基于核线约束实现立体像对中上下椭圆圆心的匹配，然后前方交会得到两个圆心的空间坐标。将其中一个圆的圆心坐标作为（X0，Y0，Z0）的初始值，将另一个圆的圆心减去它得到的向量作为圆柱中心轴线方向向量（Vx，Vy，Vz）的初始值，两个圆心的距离作为高度H的初始值。利用核线约束在两幅影像中的椭圆上找出一对匹配点，计算其三维空间坐标，该三维点与对应圆心间的距离作为半径的初始值。然后利用式（7）、式（8）计算模型坐标系和物方坐标系的旋转平移矩阵。

图5 圆柱体重建流程图Fig.5 The flow chart of cylinder reconstruction

3.2 广义点迭代平差

（1）计算参与平差的空间点的坐标。根据式（1）～式（3），分别计算立体像对中两条可见母线对应的角度θ1和θ2，利用式（10）计算顶面圆的全部离散点坐标，底面圆中θ1和θ2间的可见部分及两条可见母线上的离散点坐标。

（2）计算影像上的相应的真实轮廓点。首先将步骤（1）中计算出的空间离散点全部反投影到影像上，顶面圆和底面圆上的投影点分别拟合成椭圆，母线上的投影点分别拟合成直线。搜索椭圆法线方向上梯度变化最大的点作为该空间点对应的真实像方轮廓点，搜索母线法线方向上梯度变化最大的点作为该母线上空间点对应的真实像方轮廓点。

（3）列出参与平差的所有点的误差方程式，根据最小二乘平差计算改正数，利用改正数修正未知参数后，重复上面的步骤，直到改正数小于一定的阈值，迭代结束，得到圆柱体的精确参数。

4 试验结果与分析

为了验证本文方法的有效性，采用两个130万像素的CMOS相机组成立体相机，硬件装置如图6所示，然后利用该立体相机采集某一圆柱体工业零件的立体像对进行试验，图7为其中的一组立体像对。

图6 试验场景Fig.6 Experimental environment

图7 圆柱体工业零件立体像对Fig.7 Stereo images of cylinder industrial part

依据文献［15—16］中基于平面检校板的方法对立体相机进行检校。圆柱体7个参数的初始值（见表1第一列数据）由第3节步骤（1）计算得到，将初始圆柱体轮廓反投影到影像上，结果如图8所示。从图中可以看出初始值较好，从而保证了后面广义点平差时可以快速收敛到正确解。试验中将顶面圆和底面圆的可见部分每隔6°、可视母线间隔0.01 H计算离散采样点，利用上述广义点摄影测量的圆柱体数学平差模型及其第3节中描述的重建方法获取圆柱的各个精确参数（见表1第二列数据），反投影结果如图9所示。细部放大图见图10。从图中可以看出重建后的参数反投到影像上的轮廓与影像的真实轮廓完全地套合在一起，这表明在没有已知圆柱体的空间位置与尺寸参数的情况下，本文提出的方法能自动、正确地重建空间圆柱体。由于无法获取试验零件的设计值，本文将测量的结果与游标卡尺及文献［1］的测量结果进行比较。对10次测量平均值进行比较，结果如表2所示，表明该试验装置下检测精度能够达到±0.03mm以下。

表1 计算出的圆柱参数值Tab.1 The calculated value of cylinder parameters mm

图8 初始圆柱体轮廓反投结果Fig.8 Projection result of original cylinder contours

图9 重建后圆柱体轮廓反投结果Fig.9 Projection result of reconstructed cylinder contours

图10 重建前后细节比较Fig.10 Detail comparison between original cylinder and reconstructed cylinder

表2 重建结果平均值比较Tab.2 Comparison of average reconstruction results mm

5 结 论

试验结果表明该方法切实可行且具有很好的重建精度。另外，该方法还可方便地推广到其他具有数学模型的基本几何结构物体，如立方体、球、圆锥等。

［1］ ZHENG Shunyi，SUN Mingwei.3DVisual Measurement and Reconstruction Based on Object’s Profile in Images［J］.Acta Geodaetica et Cartographica Sinica，2006，35（4）：353－357.（郑顺义，孙明伟.基于物体成像轮廓的视觉测量与重建［J］.测绘学报，2006，35（4）：353－357.）

［2］ ZHANG Jianqing，PAN Li，WANG Shugen.Photogrammetry［M］.Wuhan：Wuhan University Press，2003.（张剑清，潘励，王树根.摄影测量学［M］.武汉：武汉大学出版社，2003.）

［3］ ZHANG Zuxun，ZHANG Jianqing.Generalized Point Photogrammetry and Its Application［J］.Geomatics and Information Science of Wuhan University，2005，30（1）：1－5.（张祖勋，张建清.广义点测量及其应用［J］.武汉大学学报：信息科学版，2005，30（1）：1－5.）

［4］ ZHANG Yongjun.Reconstruction of Circles and Round Rectangles by Generalized Point Photogrammetry［J］.Journal of Harbin Institute of Technology，2008，40（1）：136－140.（张永军.基于广义点摄影测量的圆和圆角矩形三维重建［J］.哈尔滨工业大学学报，2008，40（1）：136－140.）

［5］ HU Qi.3DVisual Measurement of Standard Sheet Metal［D］.Wuhan：Wuhan University，2005.（胡祺.标准工业钣金件三维立体量测［D］.武汉：武汉大学，2005.）

［6］ TANG Min.Key Technologies in Visual Inspection of Industrial Sheet Metal Parts with Image Sequence［D］.Wuhan：Wuhan University，2007.（唐敏.基于序列图像的工业钣金件三维尺寸视觉检测关键问题的研究［D］.武汉：武汉大学，2007.）

［7］ HAHN K，HAN Y，HAHN H.Ellipse Detection Using a Randomized Hough Transform Based on Edge Segment Merging Scheme［C］∥ISPRA’07Proceedings of the 6th WSEAS International Conference on Signal Processing，Robotics and Automation.Stevens Point：World Scientific and Engineering Academy and Society，2007.

［8］ HAHN K，JUNG S，HAN Y，et al.A New Algorithm for Ellipse Detection by Curve Segments［J］.Pattern Recognition Letters，2008，29：1836－1841.

［9］ YAO J，KHARMA N，GROGONO P.A Multi－population Genetic Algorithm for Robust and Fast Ellipse Detection［J］.Pattern Analysis and Applications，2005，8（1－2）：149－162.

［10］ XIE Y H，JI Q.A New Efficient Ellipse Detection Method［J］.Pattern Recognition，2002（2）：957－960.

［11］ FITZGIBBON A，PILU M，FISHER R B.Direct Least Square Fitting of Ellipses［J］.Pattern Analysis and Machine Intelligence.1999，21（5），476－480.

［12］ ZHANG Jianqing，SUN Mingwei，ZHENG Shunyi，et al.3DReconstruction of a Yuan Dynasty Blue－and－white Porcelain Based on Profile Constraint and Photogrammetry［J］.Geomatics and Information Science of Wuhan University.2009，34（1）：7－10.（张剑清，孙明伟，郑顺义，等.基于轮廓约束的摄影测量法元青花瓶数字三维重建［J］.武汉大学学报：信息科学版.2009，34（1）：7－10.）

［13］ ZHANG Yujin.Image Processing and Analysis［M］.Beijing：Tsinghua University Press，1999.（章毓晋.图像处理和分析［M］.北京：清华大学出版社，1999.）

［14］ QIUSHI Technology.Visual C＋＋Digital Image Typical Processing Algorithm and Implementation［M］.Beijing：Posts and Telecom Press，2006.（求是科技.Visual C＋＋数字图像处理典型算法及实现［M］.北京：人民邮电出版社，2006.）

［15］ ZHANG Yongjun.3DReconstruction and Visual Inspection of Industrial Sheetmetal Parts with Image Sequences［D］.Wuhan：Wuhan University，2002.（张永军.基于序列图像的工业钣金件的三维重建及视觉量测［D］.武汉：武汉大学，2002.）

［16］ ZHANG Yongjun，ZHANG Zuxun，ZHANG Jianqing.Camera Calibration Using 2D－DLT and Bundle Adjustment with Planar Scenes［J］.Geomatics and Information Science of Wuhan University，2002，27（6）：566－571.（张永军，张祖勋，张剑清.利用二维DLT及光束法平差进行数字摄像机标定［J］.武汉大学学报：信息科学版，2002，27（6）：566－571.）