自适应换站算法及其在长距离机载GPS动态相对定位中的应用

王潜心，徐天河，许国昌

1.中南大学地球科学与信息物理学院，湖南长沙410083；2.西安测绘研究所，陕西西安710054；3.德国地学研究中心，德国波茨坦14473

1 引 言

动态相对定位是目前高精度GPS动态定位中广泛采用的一种解算模式。根据使用参考站个数的多少，动态相对定位可分为多参考站解算模式（网解）和单参考站解算模式（单基线解）两种。网解由于充分利用了流动站周围多个参考站的观测数据，因此具有较高的精度和可靠性。相对于单基线模式而言，当个别参考站出现异常时，网解的稳定性受影响程度会大大降低。它的缺点是数据处理量大、基线相关性强、定权方法较为复杂等。尤其是在长距离机载GPS动态定位中，由于数据的采样率高、观测时间长，网解将涉及到海量观测数据的预处理、众多模糊度的固定以及抗差估计的迭代计算等，其数据处理量会非常之大。单基线处理模式则具有解算未知参数少、定权方法简单、无基线相关性以及数据处理量小等优点，因此被许多GPS动态定位软件所广泛采用［1－3］。但通常情况下，单基线处理模式是很难满足长距离精密动态定位的要求。究其原因主要是：① 许多公共误差随流动站与参考站间距离的增加，很难通过差分的方式进行有效消除；② 共视卫星数随着站间距离的增加而逐渐减少，导致定位精度下降甚至无解；③ 模糊度的解算成功率也因基线距离的增加而下降［4－5］。更换较近的参考站为新参考站无疑是解决这些问题最直接有效的办法。目前，更换参考站后新双差模糊度的求解方法共有三种：一是重新初始化模糊度；二是根据原参考站与流动站间的双差模糊度和原参考站与新参考站间的双差模糊度的关系，直接求解新参考站与流动站间的双差模糊度［6－7］；三是根据已知的卫星位置、流动站位置（由原参考站解得）以及新参考站位置，求解新参考站与流动站间的双差模糊度。

上述三种方法都各有优缺点：对于第一种方法，重新初始化模糊度会导致换站前后解的不连续；第二种方法虽然避免了重新初始化模糊度，但引入了新旧参考站间的双差模糊度。由于新旧参考站间的距离较远，因此新旧参考站间双差模糊度的解算误差会较大，并且该误差会代入新参考站与流动站间的双差模糊度中，随着换站次数的增加，误差也会一直积累。此外该方法需同时求解新旧参考站间的静态基线，使整个解算过程变得复杂；第三种方法的实质是解的融合，当函数模型或随机模型存在误差时，它不如基于原始观测信息的融合方法严格，文献［8］对此进行了详细的论述。因此寻求一种更加严格的数据处理方法，使其能实现换站前后数据的无缝拼接，保证整个动态定位过程的连续性和可靠性至关重要。

2 自适应换站法

针对单基线动态相对定位中的换站问题，提出一种自适应的换站方法，其主要思想是处理长距离机载动态定位数据时，始终保持单基线的动态定位模式，当发现流动站与原参考站间的距离大于流动站与其他参考站的距离时，自动更换周围最近的参考站为新参考站，对换站前后的数据设置一定时间的重叠段，利用参数的等价约化法［9］对换站前后的数据进行严格的自适应融合，以保证整个解算过程的连续性。其基本原理如下：

假设飞机i2从机场a飞往机场g，ag间的距离为r。机场a设有参考站i1，机场g设有参考站i4，ag间有参考站i3，如图1。

当飞机飞行一段时间后发现与原参考站i1的距离已大于与参考站i3的距离，则自动更换参考站i3作为新参考站；再飞行一段时间后发现与参考站i3的距离已大于与参考站i4的距离，则自动更换i4作为新参考站。换站时为保证解的连续性，新旧参考站间均存在一定时间的共同观测量，如图1中的bc和ef。其中称为最大限定距离，bc和ef为重叠段。

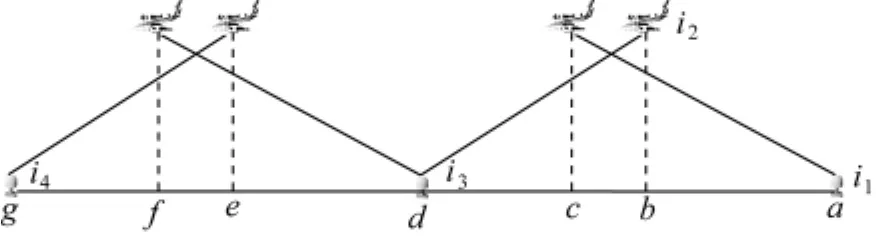
图1 自适应换站法示意图Fig.1 The schematic of adaptive changed reference station

最大限定距离和重叠段的设置主要基于如下考虑：当流动站与参考站间的距离达到一定限度后，许多与距离相关的公共误差将很难通过差分的方式进行有效地消除，此时流动站的解算精度也会随之下降，因此需要更换较近的参考站作为新参考站。最大限定距离的设置由软件自主分析并确定，软件根据用户输入的参考站坐标和伪距单点定位得到的流动站坐标，自动比较每个历元流动站与所有参考站的距离。当发现流动站与其他参考站间的距离小于流动站与原参考站间的距离时，记录下该历元，并将该历元流动站与原参考站的距离设定为一个最大限定距离。更换新参考站后将会产生新的双差模糊度，为保持解的稳定性和连续性，此时应继续保持对原参考站的跟踪直至新的双差模糊度解算成功。对新双差模糊度解算成功的辨别标准可采用方差比检验法，即当候选模糊度中最优模糊度与次优模糊度解算结果的方差比Ratio值大于用户给定值时，确认新双差模糊度解算成功。从换站开始到新双差模糊度解算成功，这段时间既有原参考站的观测数据又有新参考站的观测数据，因此称之为重叠段。自适应换站法的具体解算方法如下：

假设使用参考站i1时的双差观测方程为

使用参考站i3时的双差观测方程为

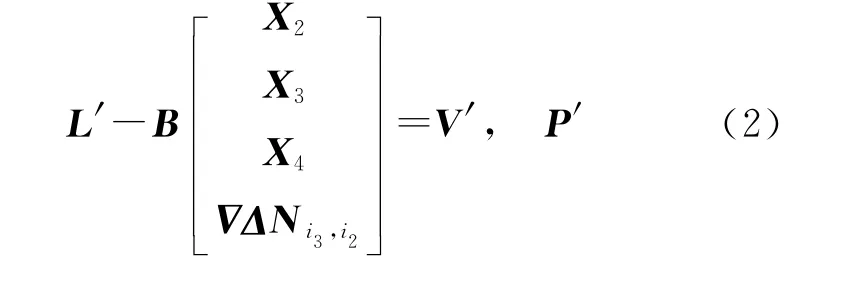
使用参考站i4时的双差观测方程为

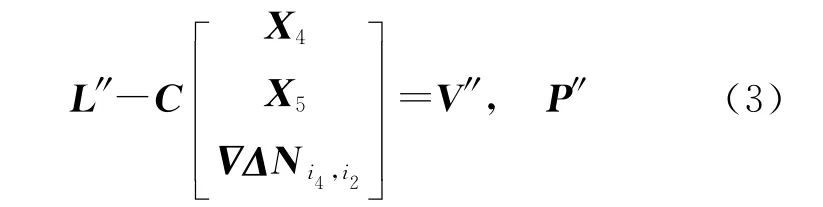
式中，L、L′、L″表示双差观测值；A、B、C为系数矩阵；X1为ab段的位置参数；X2为bc段的位置参数；X3为ce段的位置参数；X4为ef段的位置参数；X5为fg段的位置参数；ΔΔ和Δ为参考站i1、i3、i4与流动站i2间的双差模糊度；V、V′、V″为残差；P、P′、P″为权阵。

首先将式（1）写成分块矩阵的形式，

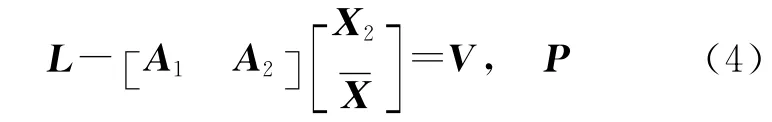
式中，

对式（5）进行等价约化可得［10］

令D1＝（E－J）A1，则有

上式为只含重叠段bc的流动站位置参数的法方程，相应的等价观测方程为

根据式（2），使用参考站i3时的法方程可写为

式中，M′＝BTP′B；U′＝BTP′L′。由于式（9）、式（11）中含有相同的流动站位置参数X2，因此可将两个法方程的对应元素进行叠加，得

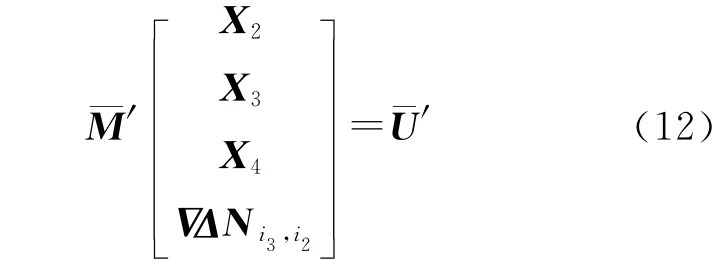
根据式（12），利用上述方法同理可得到只含重叠段ef位置参数X4的法方程

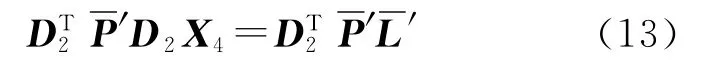
D2表达式的推导过程同前。

根据式（3），使用参考站i4时的法方程可写为

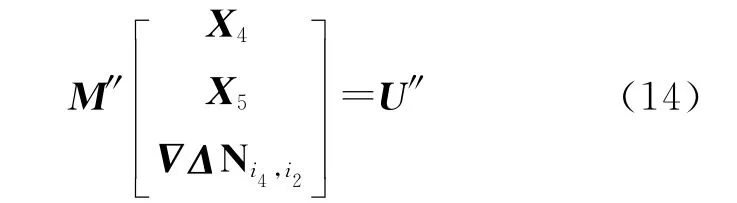
式中，M″＝CTP″C；U′＝CTP″L″。由于式（13）、式（14）中含有相同的位置参数X4，因此可将两法方程的对应元素进行叠加，得

根据式（15），利用可变参数的序贯平差［11］即可得到流动站的位置参数X4，X5以及双差模糊度ΔΔNi4，i2。最后进行回代，分别解算出使用参考站i3和i1时的位置参数和双差模糊度。为抵御粗差的影响，采用IGG3方案［12－13］进行抗差估计。

该方法相对现有方法的主要特点是：① 不用重新初始化模糊度，避免了换站前后解的不连续；② 无需求解新旧参考站间的静态基线；③ 该方法利用的是法方程的融合，即原始观测信息的融合，比基于解的融合要更加严格。另外，该方法只需在现有单基线动态定位软件的基础上增加一个子程序，即可实现长距离动态定位的功能，不会破坏原有程序的整体结构。

3 飞行动态定位试验及分析

3.1 试验数据及方法

为检验该方法的实际效果，利用一组实测的GPS机载动态定位数据进行试验。数据源于德国国家测绘局（BKG）、德国地学科学研究中心（GFZ）和德国地学环境研究所（BGR）2008年联合执行的航空重力测量项目AlpinAero2008［14］。项目从2008－09－25—2008－10－13共执行飞行20次，测区面积85 000km2，主要覆盖德国南部阿尔卑斯山区。选取其中飞行距离最远的一次飞行数据（2008－10－13）进行测试，飞机的平面轨迹如图2所示，测区内共有7个IGS站。飞行的起点和终点分别为A、B，航行距离约1 000km。起飞和降落时刻分别为13∶10∶24和17∶58∶4，采样率为1s，共17 261个历元。

图2 飞行的平面轨迹图Fig.2 Trajectory of the airplane

首先采用测区内的7个IGS站作为参考站，对流动站的位置进行网解，并将网解的结果作为“真值”。图3显示了网解的结果在NEU三个方向上的内符合精度。由图可知，该算例中网解的内符合精度约为1cm。另外由于飞机的头部和尾部分别架设了一台GPS接收机，两台接收机在地面量测的距离为5.343m。因此可以通过分别求解两台GPS接收机在整个飞行过程中的位置，并计算出它们每个历元的空间几何距离，然后与地面量测的精确距离进行比较来检验解的稳定性，结果如图4。由图可知，网解得到的平均值与地面的量测值相差约2mm，标准方差为9mm。曲线两端的波动相对较大是由于飞机在起飞和降落时机身震动较大，观测噪声相对较大所致。

为对本文所提方法和现有方法进行比较，设计了如下三个试验方案：①始终采用HUEG作为参考站，检验流动站与参考站距离越来越远时的定位情况；②依次选用HUEG、ERLA、LEIJ为参考站，换站时模糊度被重新初始化；③ 同样依次选用HUEG、ERLA、LEIJ为参考站，但换站时采用本文所提的“自适应换站”法进行解算。其中最大限定距离由软件自动分析并确定，分别为162.72km和134.43km，相应的换站时刻为第7 936历元和第12 655历元，如图5所示。算例中的Ratio值取5，两次换站后重叠段历元个数分别确定为2 919个历元和2 387个历元。试验使用的参考站情况和起止历元如表1。

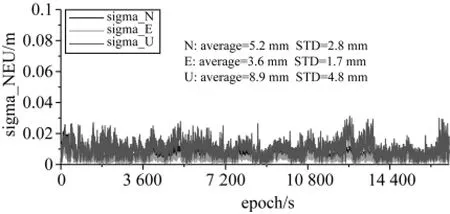
图3 网解结果在NEU三个方向的内符合精度Fig.3 The internal precision of network solution on NEU components

图4 网解得的两台GPS接收机的空间几何距离Fig.4 The distance variation between two GPS antennas

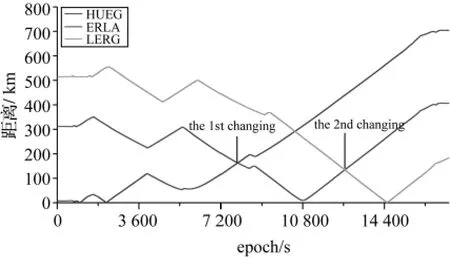
图5 飞机与三个参考站间距离的变化情况Fig.5 The distance variation between the airplane and three reference stations

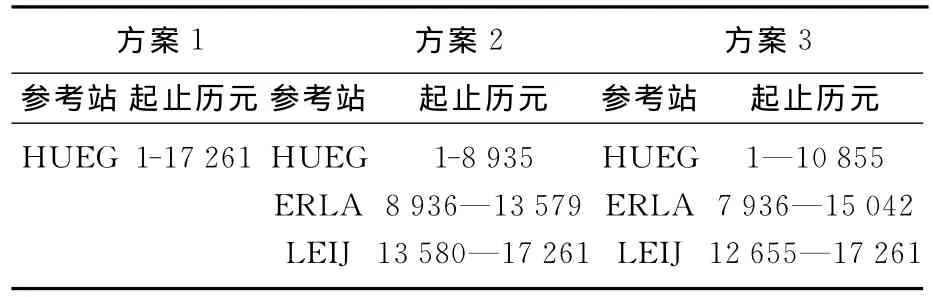
表1 试验选用的参考站及数据的起止历元Tab.1 The used reference stations and the information of used data

3.2 试验结果及分析

数据处理软件采用德国地学研究中心的HALO＿GPS精密动态定位软件［15］。解算模式为序贯平差，卫星截止高度10°，星历采用IGS精密星历，观测值使用消电离组合观测值，IGG3方案中k0＝1，k1＝5。由于机载GPS动态相对定位中流动站与参考站间高差相当大，一般达到了几公里。而对流层延迟随测站高程的变化又非常快，因此机载动态相对定位中的对流层延迟影响很难通过差分的方法将其消除。对此，对双差后剩余的对流层残差采用了附加参数估计，以抵御其影响。表2为各试验与“真值”比较，在东西、南北和高程方向上定位精度的统计结果。图6、图7、图8为各试验与“真值”比较，在三个方向上的差值及相应的双差观测值个数的变化情况。

表2 各方案动态定位精度的统计结果Tab.2 The statistical results of all the schemes cm

图6 方案1与“真值”在三个方向上差值及双差观测值个数的变化Fig.6 The differences in three components and the DD obs number of scheme 1

图7 方案2与“真值”在三个方向上差值及双差观测值个数的变化Fig.7 The differences in three components and the DD obs number of scheme 2

图8 方案3与“真值”在三个方向上差值及双差观测值个数的变化Fig.8 The differences in three components and the DD obs number of scheme 3

从表2和图6、图7、图8可知：方案1始终采用HUEG作为参考站，随着流动站与参考站间距离增加，共视卫星数逐渐地减少，定位精度也随之下降；方案2和方案3及时更换了较近的参考站为新参考站，因此有效的避免了这一缺陷；方案2在更换参考站时，模糊度被重新初始化，因此导致了换站前后解的不连续；方案3采用本文所提的“自适应换站”法，不仅避免了因飞行距离过远而导致定位精度下降，也克服了因换站引起的前后解的不连续。

4 结 论

分析了目前利用单基线处理模式进行长距离机载动态定位时存在的主要困难，提出采用“自适应换站”法来解决这一问题。其核心思想是利用等价消参法将原双差观测方程的信息完整地保存下来，通过法方程的叠加将其传递到新双差观测方程中。相对于基于解的融合以及模糊度重新初始化的这两类换站方法，自适应换站算法理论上更为严格。通过对真实飞行数据的解算，证明了该方法的可行性。计算结果表明：该方法的水平方向定位精度约为1cm，高程方向约为2cm，可满足长距离高精度动态GPS定位的需求。2011年即将启动的HALO项目将会执行上万公里的飞行任务［16］。届时若采用网解需同时处理几十甚至上百个参考站的数据，并且飞行定位中数据的采样率一般为0.1s，因此数据处理量会相当的大。采用本文所提方法将会大大减少数据处理量和软件的复杂程度。固然，利用多个参考站同时求解流动站位置要比本文所提方法的解算精度更高。但若两者的精度都在误差允许范围内，则本文无疑为GPS长距离动态定位提供了一条却实可行的思路。

［1］ CHEN Gang.GPS Kinematic Positioning for the Airborne Laser Altimetry at Long Valley California［D］.Cambridge，MA：Massachusetts Institute of Technology，1998.

［2］ XU G C，SCHWINTZER P，REIGHER C H.KSGSoft（Kinematic Static GPS Software）：Software User Manual［R］.Potsdam：GeoForschungsZentrum，1998.

［3］ HU Congwei.The Basic Models for Short GPS Baseline and Data Process Methods for GPS Kinematic Positioning［J］.Acta Geodaetica et Cartographica Sinica，2000，29（3）：282－285.（胡丛玮.GPS短基线模型与动态定位［J］.测绘学报，2000，29（3）：282－285.）

［4］ LI Bofeng，SHEN Yunzhong，ZHOU Zebo.A New Method for Medium and Long Range Three Frequency GNSS Rapid Ambiguity Resolution［J］.Acta Geodaetica et Cartographica Sinica，2009，38（4）：296－301.（李博峰，沈云中，周泽波.中长基线三频GNSS模糊度的快速算法［J］.测绘学报，2009，38（4）：296－301.）

［5］ HU G R，OVSTEDAL O，FEATHERSTONE W E，et al.Using the Virtual Reference Stations Concept for Longrange Airborne GPS Kinematic Positioning［J］.Survey Review，2008，40（307）：83－91.

［6］ XU Guochang.A Concept of Precise Kinematic Positioning and Flight－state Monitoring from the AGMASCO Practice［J］.Earth，Planet and Space，2000，52：831－835.

［7］ XU G C.GPS：Theory，Algorithms and Applications［M］.2nd Ed.New York：Springer，2007：56－57.

［8］ YANG Yuanxi，ZENG Anmin.Fusion Modes of Various Geodetic Observations and Their Analysis［J］.Geomatics and Information Science of Wuhan University，2008，33（8）：771－774.（杨元喜，曾安敏.大地测量数据融合模式及其分析［J］.武汉大学学报：信息科学版，2008，33（8）：771－774.）

［9］ ZHOU Jiangwen.∥A Collection of paper for Quasi－stable Adjustment［M］.Beijing，1987：58－63.（周江文.拟稳平差论文集［M］.北京：测绘出版社，1987：58－63.）

［10］ XU G C.GPS Data Processing with Equivalent Observation Equations［J］.GPS Solutions，2002（6）：28－33.

［11］ HUANG Weibin.Principles and Applications of the Contemporary Adjustment［M］.Beijing：PLA Press，1992.（黄维彬.近代平差理论及其应用［M］.北京：解放军出版社，1992.）

［12］ YANG Yuanxi.Robust Estimation for Dependent Observations［J］.Manuscripta Geodaetica，1994，19（1）：10－17.

［13］ YANG Yuanxi，SONG Lijie，XU Tianhe.Robust Parameter Estimation for Geodetic Correlated Observations［J］.Acta Geodaetica et Cartographica Sinica，2002，31（2）：95－99.（杨元喜，宋力杰，徐天河.大地测量相关观测抗差估计理论［J］.测绘学报，2002，31（2）：95－99.）

［14］ SCHAEFER U，LIEBSCH G，SCHIRMER U，et al.AlpinAero 2008：An Airborne Gravity Campaign for Improved Geoid Modelling in the Alps［C］∥Geophysical Research Abstracts：11.Vienna：EGU，2009.

［15］ WANG Qianxin，XU Tianhe，XU Guochang.HALO＿GPS（High Altitude and Long Range Airborne GPS Positioning Software）：Software User Manual［R］.Potsdam：GeoForschungsZentrum，2010.

［16］ FOESTE C，SCHEINERT M.HALO：A Platform for Earth Observations and Geophysics［R］.Oberpaffenhofen：GeoForschungsZentrum，2010.