基于多尺度光谱增益调制的遥感影像融合方法

刘 军，邵振峰

1.武汉大学遥感信息工程学院，湖北武汉430079；2.武汉大学测绘遥感信息工程国家重点实验室，湖北武汉430079

1 引 言

目前已有多种遥感影像融合方法［1］，最常用的是亮度－色调－饱和度（IHS）变换［2］、PCA变换［3］、Brovey变换（BT）［4］。这三个方法的优势在于能够获取到与原始全色影像（PAN）几乎一样的空间分辨率，但是最大的问题在于存在严重的光谱扭曲［5］。基于小波变换（WT）［6－9］的多分辨率分析（MRA）的引入，为改善光谱扭曲开辟了一条新的途径，因为小波变换能够在不同尺度上描述和提取影像的空间细节信息和光谱信息。但是任何方法都有它的局限性，不可能同时在空间分辨率和光谱分辨率上达到最好的效果，例如IHS、PCA和BT能够几乎完全保持全色影像的空间分辨率，但是在光谱分辨率上会有不同程度的光谱扭曲，而WT等MRA方法能够保持原始多光谱影像更多的光谱信息，但是会在不同程度上损失全色影像的空间细节信息。因此一个好的影像融合方法应该在保持空间细节和减少光谱扭曲两方面取得平衡。

在这种背景下，文献［10］提出了广义IHS（generalized IHS，GIHS）的方法，在RGB－IHS的非线性转换模型中找到了光谱扭曲的原因，并且得出是由于饱和度变化引起光谱扭曲的结论。本文在此工作的基础上，结合光谱增益曲面，提出了多尺度光谱增益调制的遥感影像融合方法。通过试验并与传统方法进行了比较，证明本文方法在平衡空间细节和光谱信息方面具有较大优势。

2 GIHS和光谱扭曲

文献［10］由RGB－IHS的线性转换公式导出GIHS公式

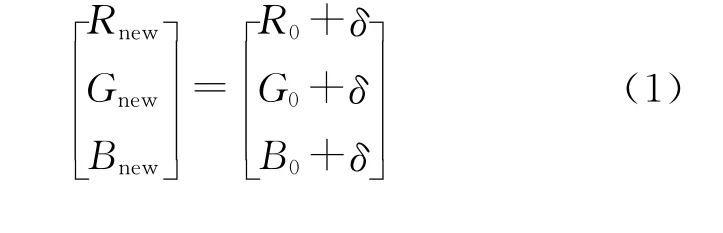
式中，（Rnew，Gnew，Bnew）为融合结果影像；（R0，G0，B0）为原始多光谱影像；δ＝Inew－I0、I0和Inew分别为原始多光谱影像亮度分量和新的亮度分量。通常在IHS变换中，Inew由全色影像对着I0进行直方图匹配而得到。常用的一些其他融合方法，如PCA变换、Brovey变换、Wavelet变换等，都可以统一归纳为GIHS方法，这便为分析这些方法的光谱扭曲原因提供了思路。根据采用的变换方法不同，Inew的表达式不同，因此δ的表达式也不同，具体可以参阅文献［10］。在另一种RGB－IHS的非线性转换关系中

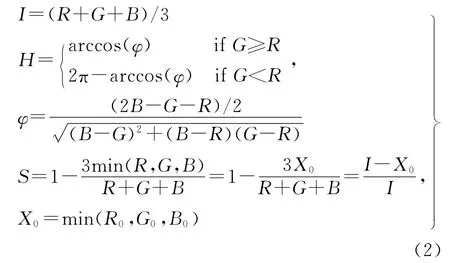
按式（2）分别计算H和S分量，可以得出：Hnew＝H0，Snew≠S0，且S的差值为

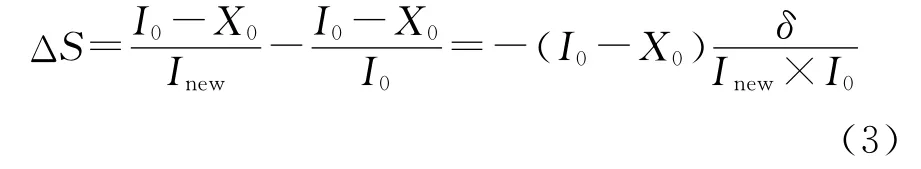
由于X0是最小值，所以I0－X0≥0，而δ不一定等于0，因此ΔS不一定等于0，从而导致融合前后饱和度发生了变化，于是便产生了光谱扭曲。而根据颜色视觉机理，色调对应于不同波长的光所引起的不同感觉，而饱和度则表示了颜色的纯度，因此，色调和饱和度可以共同描述颜色的光谱信息。从这一点可以推论出，如果能尽可能地让ΔS＝0，同时保持H不变，则可以降低由于饱和度改变而引起的光谱扭曲，从而更好地保持光谱信息。本文下面的光谱增益调制方法便是基于此思想提出的。

3 多尺度光谱增益调制融合方法

3.1 光谱增益曲面

数字影像的DN（digital number）值记录的是地物的光谱信息，在影像上表现为每个波段相应像素点位的灰度值。在RGB色彩空间中，每个像素点的灰度值向量（R，G，B）包含了该点的颜色信息，也即是光谱信息。如果在某个像素点（x，y）上，处理前的色彩灰度值为（R，G，B），处理后的色彩灰度值为（R′，G′，B′），且满足关系

式中，λ（i，j）为影像上像素点（i，j）处的增益，称为光谱增益，则处理前后的颜色保持不变，只是亮度发生了改变。所有像素点的增益构成了一个增益曲面，称为光谱增益曲面（spectrum gain surface，SGS），按照（R′，G′，B′）＝λ×（R，G，B）的方式对影像每个波段上每个像素点的DN值进行调制的方法即为本文提出的光谱增益调制方法（spectrum gain modulation，SGM），在加入全色影像的空间细节信息，保证融合影像具有高的空间分辨率的同时，保证每个像素点的DN值的色调和饱和度不变，也就保证了颜色信息不变，从而达到光谱保持的目的，因此SGM方法是一种光谱保持型的遥感影像融合算法。

这一结论可以从RGB－IHS转换模型中得到证明。从式（2）的转换关系可知：

当（R′，G′，B′）＝λ×（R，G，B）

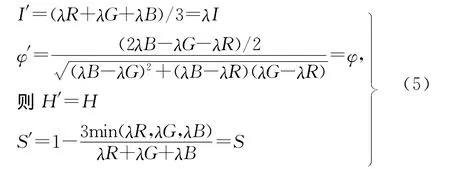
因此，色调和饱和度都没有变化，只是亮度有了一定的变化。从上节的分析可知，这一方法有助于更好地保持光谱信息。但是在实际的应用过程中，光谱增益曲面的计算是浮点运算，而DN值是0～255之间的整数，在IHS－RGB的变换中，浮点值到整数值的转换过程会出现精度损失，因此融合影像的色调和饱和度与原始多光谱影像的色调和饱和度并不可能完全一样。另外，因为亮度有了一定的变化，也会导致融合影像每个像素点的灰度值向量（R′，G′，B′）较原始多光谱影像对应像素点的灰度值向量（R，G，B）出现一定的变化，那么在影像融合质量评价过程中，基于灰度值向量的评价指标也会反映出一定的光谱扭曲，也正是因为有了亮度的变化，融合影像的空间分辨率才能得以提高。也就是说，光谱扭曲仍然会存在。但是与其他融合方法相比，本文方法的光谱扭曲要小很多，这一点可以在后面的试验中得到证实。

上面的结果可以很容易地扩展至多个波段，即在多个波段影像上，如果处理前后每个像素点的DN值满足下面的关系，也能达到保持光谱信息不变的目的。

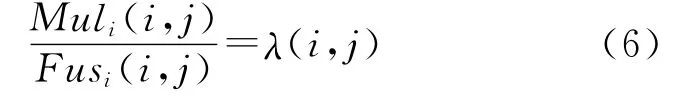
式中，（i，j）表示像素点坐标；Muli（i，j）和Fusi（i，j）分别表示原始多光谱影像和融合影像对应波段对应像素点的DN值；λ（i，j）表示该像素点的光谱增益。

3.2 单尺度光谱增益调制

将GIHS方法扩展到多个波段，可以写成

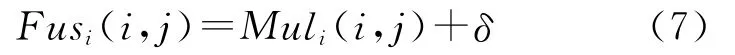
式中，Muli和Fusi分别表示原始多光谱影像和融合影像的第i波段；δ与式（1）中的δ意义相同。对IHS变换而言，δ＝Inew－I0，可以理解为新的亮度分量与原始亮度分量的差异，也即是空间细节之间的差异。但是经过直方图匹配后全色影像（也即是新的亮度分量Inew）会改变一部分的空间细节信息。由于多光谱影像也具有一定的空间细节信息，因此在提取全色影像特有的空间细节信息时，需要去除多光谱影像的空间细节信息。

高斯函数具有低通性质，可以用来提取原始影像特有的空间细节信息，同时，它是一种模拟人眼视觉机理的理想数学模型，设定不同的尺度参数σ，即能够模拟人眼从远处到近处所看到的图像。高斯函数的表达式为

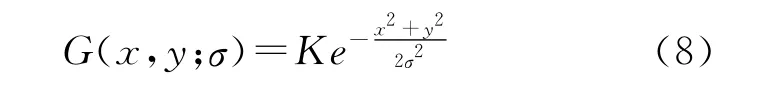
式中，σ为高斯函数的尺度参数，系数K由归一化函数决定。

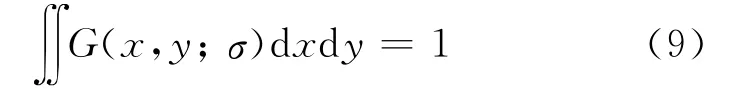
将高斯函数与影像进行卷积，可以得到影像的低频信息，从原始影像上减去低频信息，即可得到高频细节信息。因此Pan－G（x，y；σ）＊Pan和I－G（x，y；σ）＊I分别表达了全色影像和多光谱亮度分量的空间细节信息，其中Pan和I分别表示全色影像和多光谱亮度分量，＊表示卷积操作，则Pan－G（x，y；σ）＊Pan－（I－G（x，y；σ）＊I）描述的空间细节差异即为提取出的全色影像特有的空间细节信息。结合光谱增益曲面，本文提出的单尺度光谱增益调制（single－scale spectrum gain modulation，SSGM）影像融合方法表达式为

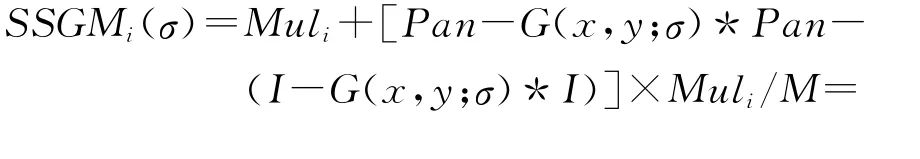
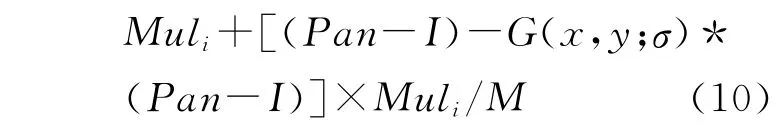
若令κ＝［（Pan－I）－G（x，y；σ）＊（Pan－I）］／M，可得

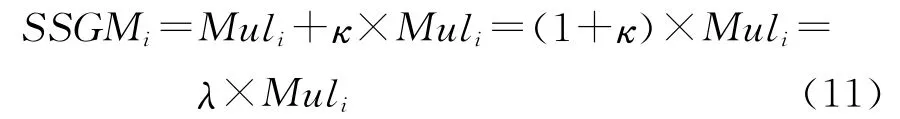
在每个像素点上计算SSGM输出时，有可能λ（i，j）×Muli（i，j）大于255或者小于0，此时该像素点的光谱增益需要做如下的调整，以保证新的SSGM输出值在0～255之间。

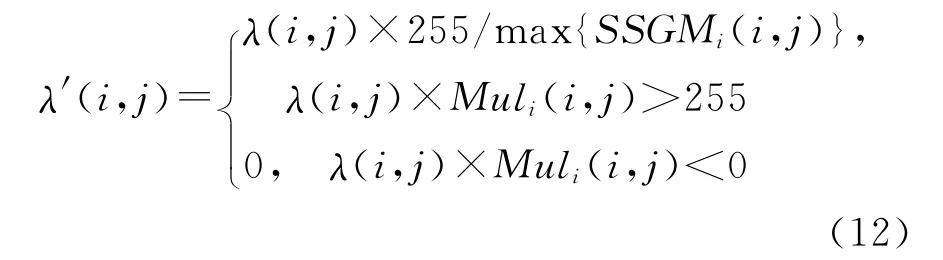
式中，SSGMi（i，j）为由调整之前的光谱增益值计算出的当前像素点各波段的灰度值。

SSGM中提取空间细节信息的物理意义是用原始影像减去高斯函数与原始影像的卷积，实际上是减去了原始影像的低频部分，留下的是高频细节。由于加入到多光谱影像中的是全色影像特有的空间细节信息，因此不需要将全色影像对着多光谱影像亮度分量进行直方图匹配，从而更有效地保全了多光谱影像的光谱信息。高斯函数窗口r和尺度参数σ会直接影响到保留的高频细节的成分，进而影响融合结果影像的空间分辨率。当窗口r越大，保留的高频细节信息越多，空间分辨率越高，但计算量越大，光谱信息保留得越少，光谱分辨率越低，反之亦然。因此，为了取得好的融合效果，需要选择一个适中的尺度参数。

另外，对于服从参数为μ，σ的高斯分布的随机变量来说，其值几乎完全落在［μ－3σ，μ＋3σ］的区间内。根据这个“3σ规则”，在高斯滤波器中，离滤波器中心点越近的像素点其权重越大，超过3σ距离的像素点权重基本上可以忽略不计。实验表明，当r＝3σ时，能够在空间分辨率与光谱分辨率之间取得一个较好的折中。因此本文中的尺度参数均满足r＝3σ的关系。

3.3 多尺度光谱增益调制

研究发现，对SSGM而言，尺度越小，越能保存更多的光谱信息，但是损失的空间细节信息越多；反之尺度越大，保护空间细节信息的能力越强，但是会失去更多的光谱信息。由于单尺度光谱增益调制无法完全满足影像融合的要求，因此本文在SSGM的基础上提出了多尺度光谱增益调制（multi－scale spectrum gain modulation，MSGM），使其具有SSGM在高、中、低三个尺度上的均衡特性。

MSGM的基本公式为

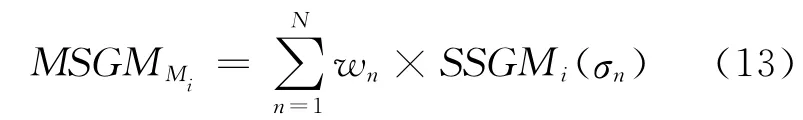
式中，MSGMMi为融合影像第i波段的输出；N为尺度个数，本文中N＝3；SSGMi（σn）为原始影像多光谱影像第i波段的尺度为σn的SSGM输出；wn为SSGMi（σn）的权重，满足般可取wn＝1／N。

从式（13）可以看出，当N＝1时，MSGM即弱化为SSGM。通过设置不同的σn和对应的权重，可以根据实际需求得到不同的融合效果，从而在空间分辨率与光谱分辨率之间达到一个较好的均衡。

4 试验与分析

作者选取北京某地区的IKONOS影像作为试验影像，选取可见光RGB三个波段合成的真彩色影像作为输入的多光谱影像，空间分辨率为4m，全色波段的空间分辨率为1m。全色影像的大小为512×512像素，如图1（a）所示，图1（b）为同一地区的经过配准和重采样后的多光谱影像，图1（c）～（i）为采用IHS、PCA、BT、三种尺度的SSGM和MSGM方法得到的融合多光谱影像。

图1 IKONOS影像融合结果Fig.1 Fusion results of IKONOS images

与多光谱影像相比，从光谱分辨率上可以很明显地看出，前三种方法存在着明显的光谱扭曲，例如在方框和椭圆框标出的区域，IHS、PCA和BT三种方法的颜色与多光谱影像相比，存在比较大的偏差；而其他几种方法保持的光谱信息要好很多，基本上看不出颜色偏差。对于SSGM方法，随着尺度参数σ由1增大到9，空间分辨率得到了很大的提高，但是光谱偏差也随之增大。

由于目前对融合结果的定量评价方法很多，大部分都是基于统计方法，而且各方法的评价结果不一定完全一致，因此本文仅选取最常用的相关系数［11］来对文中各方法做定量评价。表1是计算的光谱相关系数和空间相关系数的值，表中SSMG1、SSMG3、SSMG9分别表示σ＝1、σ＝3、σ＝9时的SSMG融合影像。

从表1可以看出IHS、PCA和BT方法的光谱相关系数比较接近，SSMG受尺度参数的影响，各尺度之间有一定的差距，但仍比IHS、PCA和BT的要高很多。这说明前三种方法的光谱扭曲度是最大的，其中BT的光谱扭曲最严重。尺度参数越小，SSMG保持光谱的能力越高，随着尺度参数的增加，SSMG保持光谱的能力逐渐减弱。MSMG是多个尺度参数综合作用的结果，因此光谱相关系数相对于多个SSMG来说比较折中。

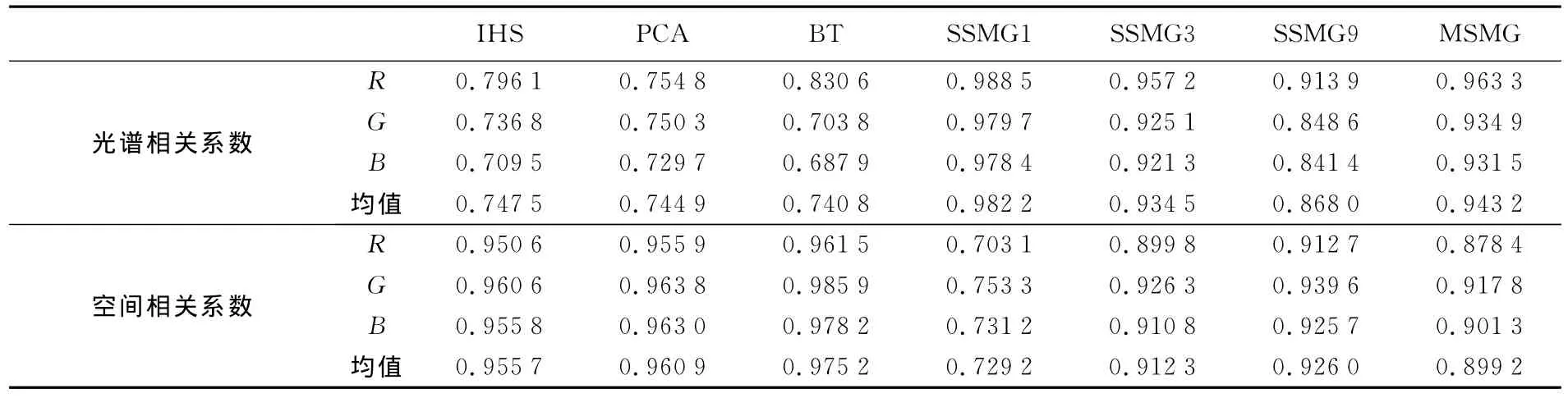
表1 相关系数Tab.1 The correlation coefficient

IHS、PCA和BT的空间相关系数相差不大，其中PCA最高。这说明这三种方法在保持空间细节的能力上更优。尺度参数越大，SSMG保留的空间细节信息越多，σ＝9时的值要远高于σ＝1时的值。与光谱相关系数类似，MSMG的结果仍然是多个SSMG的折中。

为进一步研究尺度参数对融合结果的影响，本文将尺度参数从σ＝1递增到σ＝9，重新计算光谱相关系数和空间相关系数，结果如图2的折线图所示，横坐标是尺度参数，从图中也可以很明显地看出随着尺度参数的增加，光谱相关系数逐渐降低，而空间相关系数则升高。这是因为随着尺度参数的增大，保留的空间细节信息更多，被修改的光谱信息也更多。

结合表1和图2可知，对于一种方法，如果光谱相关系数高，则空间相关系数必然低，反之亦然。这是因为空间信息保留得越多，那么失去的光谱信息也越多。因此只能在光谱分辨率和空间分辨率上做一个折中的取舍。MSMG正是为这一折中而设计的方法，虽然它的空间分辨率和光谱分辨率均不是最高，但却是一个比较好的折中，而且本文中可以通过改变尺度参数和相关权重来调整空间质量和光谱质量，以满足各种不同的应用需求。

为验证本文方法的正确性，作者使用Quick－Bird影像做了另外一组试验。全色影像的空间分辨率是0.61m，影像大小为1 000×1 000像素，多光谱影像的空间分辨率为2.44m，MSMG采用的三个尺度分别是3、9、27，融合结果如图3所示。

图3 QuickBird影像融合结果Fig.3 Fusion results of QuickBird images

从图3可以看出，IHS、PCA、BT变换三种方法都存在较严重的光谱偏差，而MSMG的光谱与原始多光谱影像非常接近，同时从空间细节上，这四种方法看不出明显的差别。定量比较的结果如图4所示。从图4的柱状图可以很明显地看出，MSMG方法在光谱相关系数上远高于其他方法，空间相关系数与IHS和PCA接近，BT的空间相关系数的均值最高，但同时BT的光谱相关系数的均值却最低。从综合上来看，MSMG方法的融合效果是最好的，这一结论与IKONOS融合试验的结论是一致的。

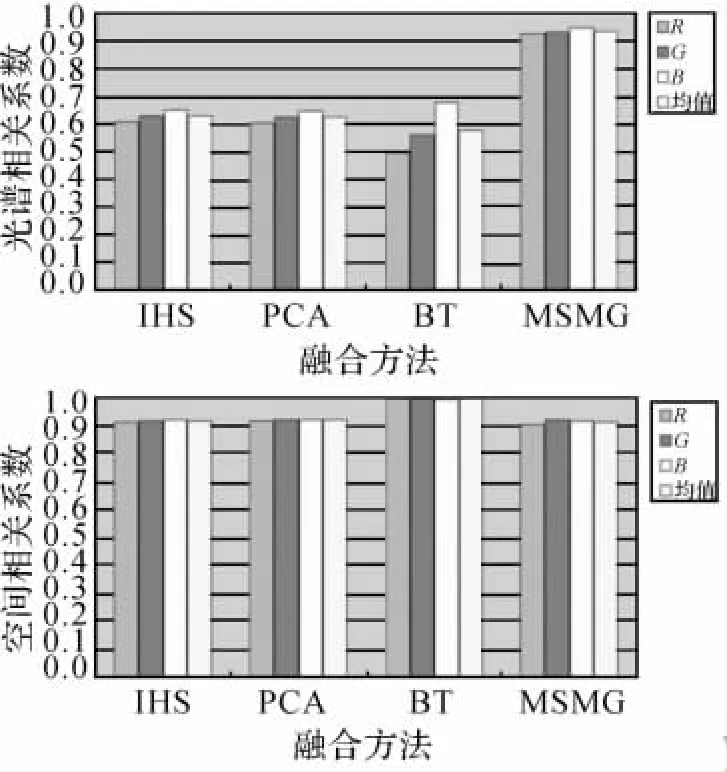
图4 QuickBird影像融合质量评价结果Fig.4 Quality evaluation results of QuickBird image fusion

笔者也用其他传感器影像如SPOT、World－View－2影像做了类似的试验，可以得出与文中一样的结论。为取得更好的融合结果，可以根据实际应用的需求，在采用MSMG方法时需要选择合适的尺度参数及加权系数。因为当尺度参数越大，则卷积窗口越大，计算量可能成倍地增加，因此需要在尺度参数与融合结果之间做一个平衡的选择。

5 结论与展望

本文比较了当前几种常用方法，并针对广义IHS变换中存在的由于饱和度改变而导致的光谱扭曲问题，基于光谱增益曲面，提出了一种基于多尺度光谱增益调制的光谱保持型影像融合方法，有效减少由于饱和度改变引起的光谱扭曲。与传统方法不同的是，该方法中不需要将全色影像进行直方图匹配，因此更能保护全色影像的空间细节信息。该方法用于IKONOS和QuickBird全色和多光谱影像的融合试验中，能够得到清晰且光谱保真度高的融合影像，在空间质量和光谱质量之间取得了一个比较好的平衡，适用于对光谱保持有较高要求的应用场合。

［1］ DOU Wen，CHEN Yunhao，HE Huiming.Theoretical Framework of Optical Remotely Sensed Image Fusion［J］.Acta Geodaetica et Cartographica Sinica，2009，38（2）：131－137.（窦闻，陈云浩，何辉明.光学遥感影像像素级融合的理论框架［J］.测绘学报，2009，38（2）：131－137.）

［2］ CHU Heng，ZHU Weile.Fusion of IKONOS Satellite Imagery Using IHS Transform and Local Variation［J］.IEEE Transactions on Geoscience and Remote Sensing Letters，2008，5（4）：653－657.

［3］ SHAH V P，YOUNAN N H，KING R L.An Efficient Pan－sharpening Method via a Combined Adaptive PCA Approach and Contourlets［J］.IEEE Transactions on Geoscience and Remote Sensing，2008，46（5）：1323－1335.

［4］ CHEN Shaohui，ZHANG Renhua，SU Hongbo，et al.Scaling－up Transformation of Multisensor Images with Multiple Resolutions［J］.Sensors，2009，9（3）：1370－1381.

［5］ LAPORTERIE－DÉJEAN F，DE BOISSEZON H，FLOUZAT G，et al.Thematic and Statistical Evaluations of Five Panchromatic／Multispectral Fusion Methods on Simulated PLEIADES－HR Images［J］.Information Fusion，2005，6（3）：193－212.

［6］ CHIBANI Y，HOUACINE A.Redundant versus Orthogonal Wavelet Decomposition for Multisensor Image Fusion［J］.Pattern Recognition，2003，36（4）：1785－1794.

［7］ OTAZU X，GONZáLEZ－AUDíCANA M，FORS O，et al.Introduction of Sensor Spectral Response into Image Fusion Methods.Application to Wavelet－based Methods［J］.IEEE Transactions on Geoscience and Remote Sensing，2005，43（10）：2376－2385.

［8］ HILL P，CANAGARAJAH N，BULL D.Image Fusion Using Complex Wavelets［C］∥Proceedings of the British Machine Vision Conference.Cardiff：BMVA Press，2002：487－496.

［9］ LI S，KWOK J T，WANG Y.Using the Discrete Wavelet Frame Transform to Merge Landsat TM and SPOT Panchromatic Images［J］.Information Fusion，2002，3（1）：17－23.

［10］ TU T M，SU S C，SHYU H C，et al.A New Look at IHS－like Image Fusion Methods［J］.Information Fusion，2001，2（3）：177－186.

［11］ ZHOU J，CIVCO D L，SILANDER J A.A Wavelet Transform Method to Merge Landsat TM and SPOT Panchromatic Data［J］.International Journal of Remote Sensing，1998，19（4）：743－757.