考虑区域构造特征的地壳形变分析拟合推估模型

赵丽华，杨元喜，王庆良

1.长安大学地质工程与测绘学院，陕西西安710054；2.西安测绘研究所，陕西西安710054；3.中国地震局第二监测中心，陕西西安710054

1 引 言

最小二乘拟合推估，又称最小二乘配置，根据最小二乘推估来内插和外推重力异常［1］。近年来，国内外众多学者基于拟合推估法开展大量的地壳形变分析研究。文献［2—3］将其用于地壳垂直形变速度场的研究，认为该方法是研究构造变形的有利工具；文献［4］应用拟合推估方法研究日本东京地区水平运动形变场，验证该方法可以排除观测噪声干扰，分离出所需要的形变信号；文献［5］对华北盆地154个GPS观测速度运用拟合推估方法得到连续的速度场，计算该地区的应变分布，并与传统的离散三角法相比较，得出拟合推估方法能更清楚地反映出地壳的形变状态；文献［6—9］在地壳形变分析时均采用拟合推估方法内插位移向量来计算应变场；文献［10］提出一种改进的拟合推估法，根据趋势项的梯度迭代计算协方法差函数，从而提取非随机形变场的趋势项与形变信号。这些文献将拟合推估法应用于地壳形变分析时，大都假设被拟合参数在空间是连续变化的。事实上对于大尺度、地壳运动复杂的形变场，由于小断层或隐伏断层的存在，形变的连续介质中常常存在着若干非连续面，若仍按统一的拟合推估模型进行形变分析，则会扭曲形变分析结果，因为统一的拟合推估模型只能给出形变（应变）场在空间域的总体变化趋势，在断裂附近只能给出一个连续的光滑结果。如此，很难合理地描述不同活动块体间的运动（或变形）差异。

一般认为，由断层分割的各区域块体的运动方式和大小具有整体上一致趋势。但由于观测异常误差或块体内部非均匀变形，使同一块体内有些观测点上的位移观测值表现得“不合群”，这些点会导致形变参数解有偏，一般不宜参与块体整体运动参数计算。由于局部非均匀变形和干扰会影响块体实际的运动和变形参数精度，采用高崩溃污染率抗差估计方法［11］，将这些显著变形或受异常误差干扰的观测值判别筛选出来。筛选之后的点组即为相对稳定点组，如此建立的块体整体运动模型，可望较合理地反映块体整体运动趋势。

2 相对稳定点组的确定

如引言所述，在建立块体的速率模型时，为提高模型的可靠性，同一块体内部具有异常形变的点不宜参与建模，一般将这些异常观测和非均匀变形看作对所在块体整体位移和变形的一种干扰，或者说是“粗差”将其剔除［12－13］。这里采用抗差估计的方法来确定块体内运动相对平稳的点。但一般抗差估计方法在迭代计算中，参数的初值一般为相应的最小二乘解。当观测值出现异常时，形变参数的最小二乘解会有较大偏离，从而使后继的残差值偏离，等价权也随之失效。为此，寻求一种崩溃污染率较高的参数估值，即当观测值中有较多异常或较大异常时，参数估值不至受到太大影响，从而为后续的抗差等价权的确定提供可靠的测值残差。可采用如下算法：

（1）将各点速率观测值分别取中位数med（L），求各速率值与相应中位数之差，即初始残差

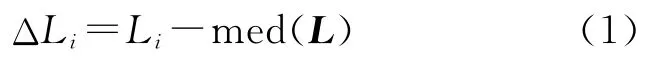
（2）计算ΔL的均方差因子抗差解［14－15］

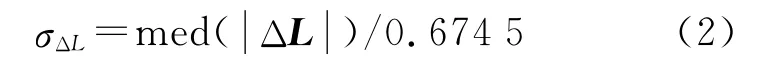
基于此式求得的变形参数抗差解具有50%的高崩溃污染率［11］。

（3）取强淘汰函数

式中，k0可取1.0或1.5。

（5）进行后继M估计迭代计算。考虑到观测速率的相对稳定性，权函数IGG方案做了如下调整［11］

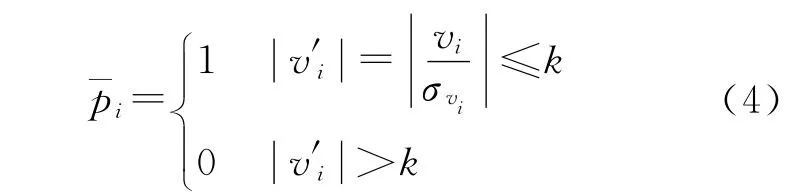
式中，k＝1.5～2。

迭代结束后等价权为0的观测值即为异常观测，其余点即为相对稳定点组参加后继的分区域拟合推估模型的建立。

3 块体运动模型的精化及相邻块体边界的确定

对于大尺度、地壳运动复杂、小断层或隐伏断层比较多的形变场，若按通常的拟合推估方法建模，对于分布在断层两侧的点，只能根据速度场在空间域的总体变化趋势进行平滑处理，其结果不能正确地反映断层附近形变的真实情况。因此，根据所研究区域的地质构造特征，建立区域运动拟合推估模型。

（1）利用已有地质资料按断层分布将研究区域划分为若干块体。相邻断层附近界限不明的点不参与划分，等候判别。按前述方法找出各区域内相对稳定的点组，利用拟合推估原理建立如下区域运动模型［16－17］

式中，L为沿坐标轴的速度分量；A、B为设计矩阵；β为非随机参数向量；Δ为观测误差向量，Δ～N（0，ΣΔ）；S为已测点上随机信号向量，S～N（0，ΣS）；ΣΔS＝0，即Δ与随机参数S不相关。Aβ为系统形变，反映块体运动的一般趋势；BS为随距离变化的随机函数，反映块体内连续的、不规则的形变。这里S是以单点信号的形式出现的，所以B为单位阵。为推估未测点上信号，将式（5）改写为

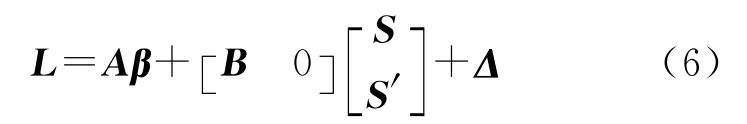
式中，S′为推估点上信号，S′～N（0，ΣS′），且基于最小二乘原则可得

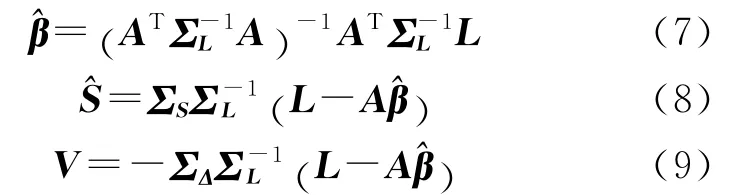
式中，ΣL＝ΣΔ＋BΣSBT，为观测值协方差矩阵。任一未测点上信号则为

（2）根据测量误差的性质，设V服从正态分布，分别对不同分块中的V进行区间估计。给定置信概率为1－α＝0.90，则V的置信下限Vlow和置信上限Vup分别为［18］

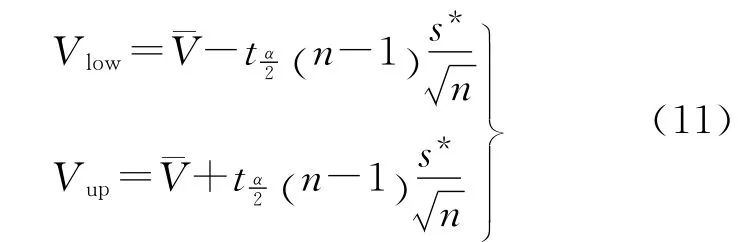
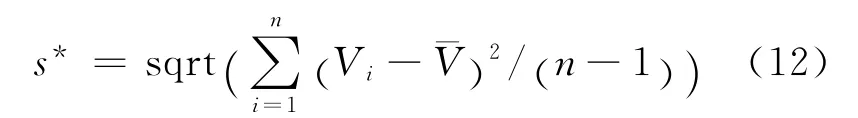
则（Vlow，Vup）即为模型残差的置信区间。

（3）选取边界附近的点进行判别。将断层附近分界不明的点作为检验点，分别用各区域的拟合推估模型推估其形变量，计算预测残差，即推估值与观测值较差

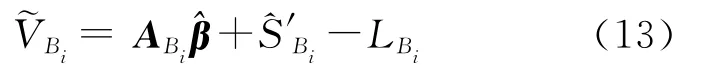
式中，LBi表示边界上点Bi的观测值；ABi、＾S′Bi分别表示该点对应的形变参数系数阵和信号。

（4）假设检验

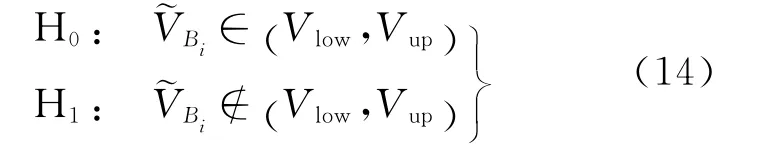
若H0成立，则将Bi点添加到相应块体的稳定点组。

（5）用新组成的稳定点组重复（1）～（4）的计算。

迭代的过程即是对形变模型精化的过程，同时也确定了断层边界的分布。

4 计算与分析

4.1 算例1

模拟一个100km×100km的垂直位移形变场，其内部100个监测点坐标由随机函数生成；同时假设一条断层穿过该形变场，将形变场分割为区域1和区域2两部分（图1）。给位于区域1的监测点赋予2mm／y的速率，位于区域2的监测点赋予1mm／y的速率，并且加入均方差为1× 10－6的正态随机误差。把随机误差和固定速率相加得到监测点垂直位移速率的模拟观测值。若考虑由已有地质资料所判断的断层的位置可能存在的不确定性，将模拟断层附近的20个点作为分界不明的点等候判别；另外，为检核拟合推估的精度，在区域1、区域2中随机均匀选取19个点作为外部检核点，检核精度的均方根误差公式为

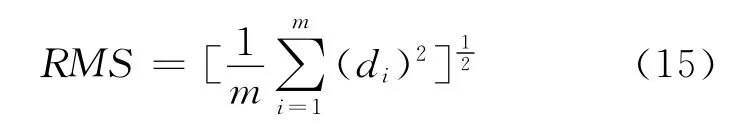
式中，m为检核点个数；di为检核点不符值，是拟合模型模拟的检核点速率与该点实测速率之差。

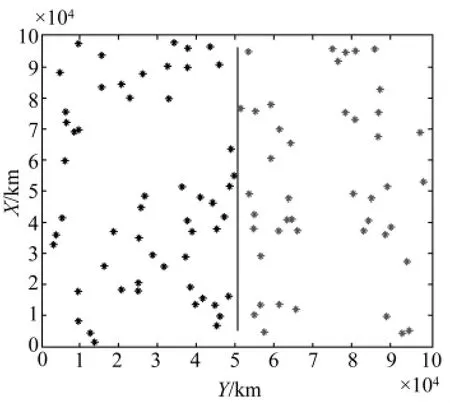
图1 模拟观测点及断裂分布Fig.1 The distribution of simulated measurement points and fault

为比较分析高崩溃污染率抗差估计法确定相对稳定点组的有效性，试验采用两种方案进行。

方案1：无异常数据影响情形。分别采用一般拟合推估方法；根据地质资料的分区域拟合推估法；基于稳定点组的分区域抗差拟合推估法。

方案2：有异常数据影响情形。各区域分别随机选取四个点人为加入2mm～3mm的异常值，进行与方案1完全相同的计算。

图2、图3分别表示两个方案中不同方法计算得到的垂直形变场空间分布图；不同方法估计的检核点均方根误差列于表1；图4为两种方案中各拟合模型检合点不符值分布。

表1 不同方案计算结果比较Tab.1 Comparison of different methods mm

分析上述计算结果可发现：

（1）一般拟合推估方法得到的形变场在断层附近只是将非连续面间的点值进行光滑，没有合理反映形变的真实情况，使推估的形变量有较大偏差（图2（a）），而分区域拟合推估法（图2（b））和分区域抗差拟合推估法（图2（c））在方案1没有异常数据的影响下都较好地反映出断裂活动及块体间运动差异，较真实地反映区域的形变特征。

（2）当观测存在异常时，一般拟合推估法（图3（a））和分区域拟合推估法（图3（b））受异常数据的影响非常大，由这两种方法得到的形变场空间分布图形与图2（b）和图2（c）中相应图形相比，存在显著偏差；而分区域抗差拟合推估法（图3（c））仍然较好地反映研究区域真实的形变特征，与方案1图形非常一致，反映出该方法良好地抵制异常数据影响的能力。

（3）从外部检核结果可以看出（图4），一般拟合推估方法推估的未测点形变量与其真实形变差异较大；而不论是一般拟合推估还是分区域拟合推估，在异常数据的影响下（方案2），检核点不符值变化都比较大，反映出未测点推估值的误差较大。分区域抗差拟合推估则较好地抵制异常值的影响，检核点不符值整体上较为均匀地分布于0值附近，均方根误差明显降低。

（4）从表1中也可以看出，无论有无异常污染，分区域抗差拟合推估解都基本一致，外部检核点均方根误差都比较小，且大致相等，反映出该方法具有较好的稳定性。这说明当采用高崩溃污染率抗差估计方法对观测值中的异常值进行筛选后，分区域拟合推估模型能更好地逼近未测点的真实值。

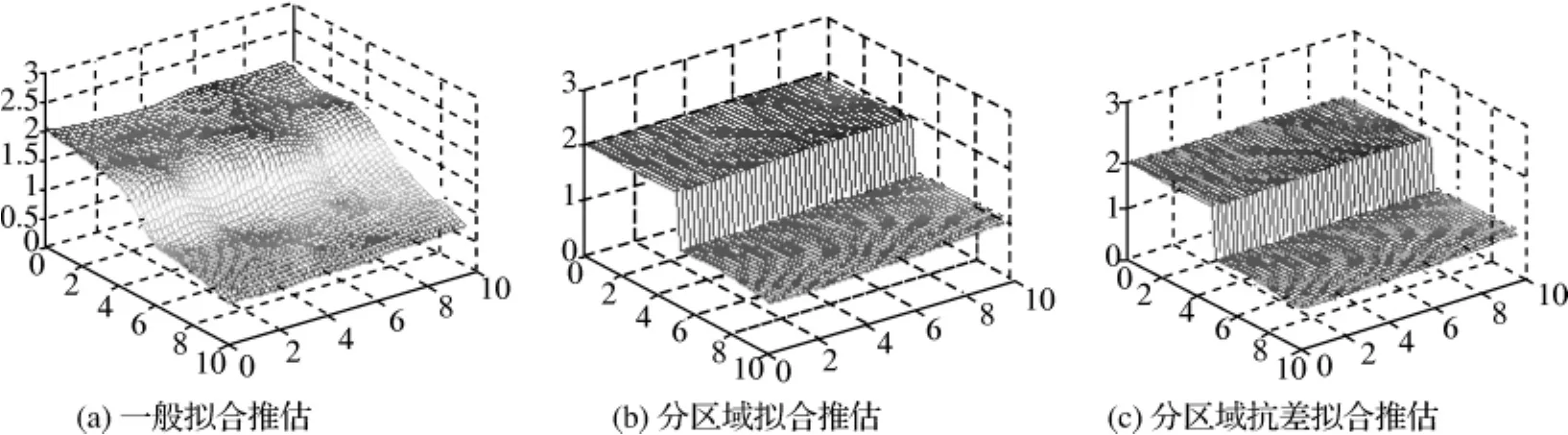
图2 方案1中不同计算方法得到的垂直形变场空间分布图Fig.2 Vertical velocity fields by different methods in case 1

图3 方案2中不同方法得到的垂直形变场空间分布图Fig.3 Vertical velocity fields by different methods in case 2

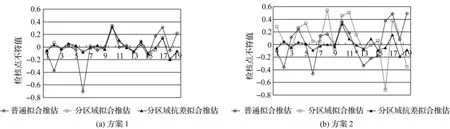
图4 各方案检核点不符值Fig.4 Residuals of check points

4.2 算例2

实测数据为100°E～110°E，33°N～37°N区域中100个GPS站点的速率及相应中误差，点位分布及速率见图5。该数据由中国地震局第二地形变中心于1999－07月和2001－07月分别采用Z－型GPS接收机观测所得，该观测网位于青藏高原东北缘，是国家重大科学工程“中国地壳运动观测网络”的一部分。对该GPS网进行每站96h蛙跳式观测，相应数据与中国大陆及周边约15个IGS站进行同步解算，分别采用GAMIT软件和GLOBK软件进行统一处理。

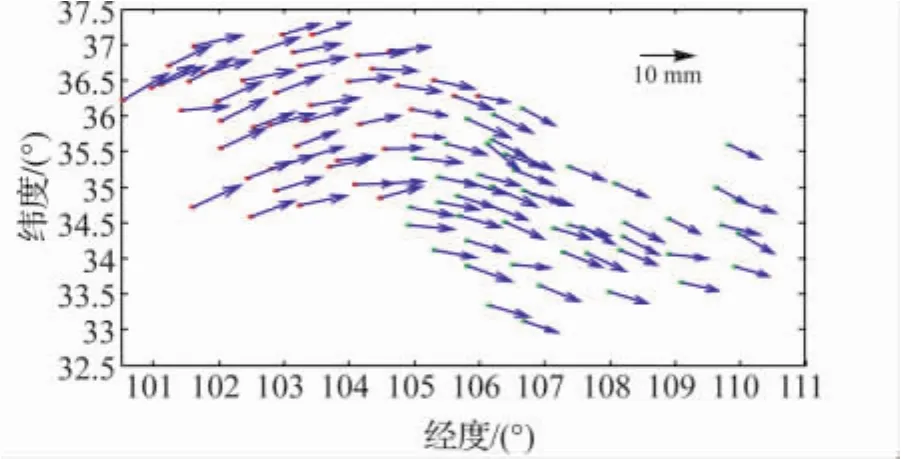
图5 各点位置分布及速率Fig.5 Distribution and velocity of observation points

根据晚第四纪活动断裂带分布情况，固关—功县断裂带从该区域通过［19］。根据此断裂带对该区域概略划分为A区、B区，对分布于断裂带附近的19个点进行检验判别。对该区域形变模型的建立采用如下两种方案：① 一般拟合推估法；②本文提出的分区域抗差拟合推估法。

为说明新方法的有效性，将两种方案得到的模型拟合误差列于表2，同时将边界点判别归区前后各区的拟合误差列于表3。拟合误差由拟合残差的均方根误差表示

式中，V为模型拟合残差向量；m为拟合点的个数。

外符合精度检核则在区域中均匀选取27个点作为外部检核点不参与计算，通过以上两种方案分别模拟其速率值。由这些点的模拟值与已知值（观测速率）之差，根据式（14）计算检核点的均方根误差并列于表4；将不同计算方案模拟的各检核点水平运动速度与相应实测值进行比较，比较结果见图6。

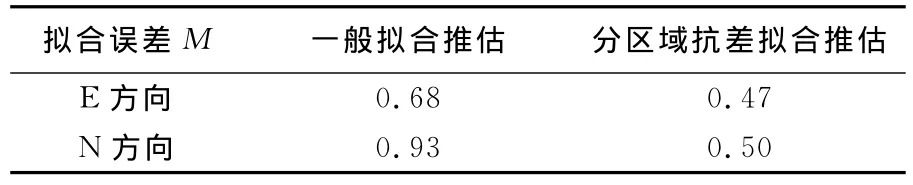
表2 不同方案模型拟合误差MTab.2 Mof different cases mm

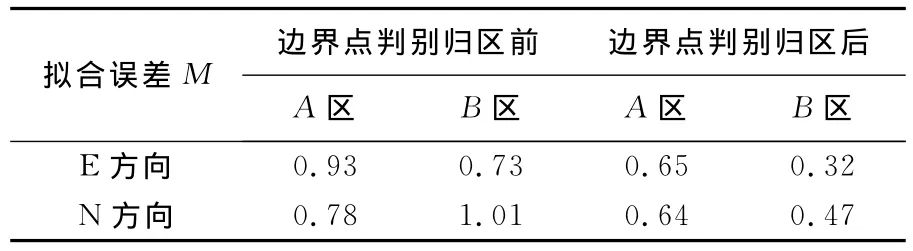
表3 边界点判别前后各区拟合误差MTab.3 Min area Aand B mm

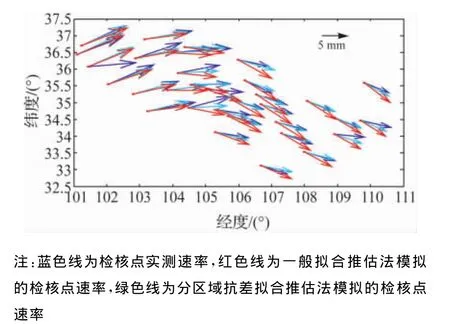
图6 算例2中不同方案模拟的水平运动与实测值比较Fig.6 Comparison between simulated velocity and observed velocity

从计算结果中可以看出：

（1）分区域抗差拟合推估模型的拟合误差明显小于一般拟合推估模型（表2），说明该模型能更合理的描述此类区域的变形特征。

（2）受不同区域运动差异影响，边界上的点在判别归区之前，各区的拟合RMS都比较大，而经过合理的归区后，拟合均方根误差明显减小（表3）。实际上，在判别归区前，边界点在各区的残差表现出明显的区域特征，如有7个点在A区中具有较大残差而在B区中残差较小，同时A区中残差较小的8个点在B区中具有较大误差，体现显著检验的效果。

（3）一般拟合推估方法，由于要反映形变场在空间域的整体变化趋势，对不同块体运动差异的描述显得较为粗略，由此求得的点位形变的精度相对较低（图6）；分区域抗差拟合推估法由于顾及不同块体各自的运动特征，拟合效果明显提高，在一定程度上反映断裂活动和块体运动差异，求得的点位形变与各点的实测值具有较好的一致性（图6）。

（4）由于篇幅限制，没有一一列出各检核点不符值（拟合模型估计的检核点速率与该点实测速率之差），但由检核点不符值计算的RMS也反映出分区域抗差拟合推估法估计的各点水平运动速率更接近真实值（表4）。

（5）分区域抗差拟合推估法在确定块体运动模型的同时，还确定块体边界分布（图5中用测站点的不同颜色来反映区域划分边界）。这与该地区地质情况和块体划分一致［19］。

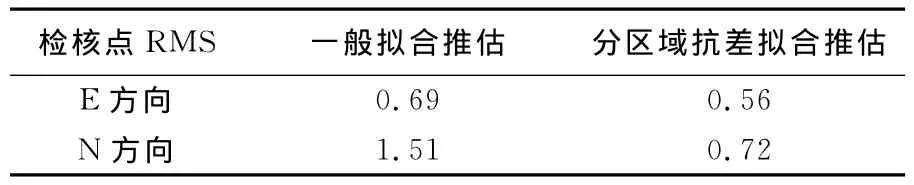
表4 不同方案检核点RMSTab.4 RMS of check points mm

5 结 论

若形变场中有隐伏断层或存在较显著形变差异时，有时无法确切地知道差异运动的分界带。这时若采用一般拟合推估方法建立形变场，在断层附近会产生较大偏差，无法可靠地反映断层分布情况。本文首先通过地质资料进行简单判断，对可能存在断层的区域进行概略划分，然后通过高崩溃污染率抗差估计法挑选各区域内相对稳定的点，建立各区域形变场置信区间。对分布在断层附近分界不明点的归属进行判断，确定各块体差异运动的边界。边界明确后，分别建立各区域能够描述本块体运动趋势的拟合推估模型，计算区域形变场。试验算例表明，该方法在发现隐伏断层并确定其分布边界的同时，建立的形变场较好地表现出不同运动块体边界上的差异运动，具有较高推估精度。当研究区域观测点数量相对较少时，利用此方法解得的形变参数可以推算任意未测点的形变量，达到分析形变和应变的目的。

［1］ KRARUP T.Mathematical Foundation of Geodesy：Selected Papers of Torben Krarup［M］.Berlin：Springer，2006：29－90.

［2］ FUJII Y，XIA S.Estimation of Distribution of the Rates of Vertical Crustal Movements in the Tokai District with the Aid of Least－squares Prediction［J］.Journal of Physics of the Earth，1993，41（4）：239－256.

［3］ EL－FIKY G S，KATO T，FUJII Y.Distribution of the Vertical Crustal Movement Rates in the Tohoku District，Japan，Predicted by Least－squares Collocation［J］.Journal of Geodesy，1997，71（7）：432－442.

［4］ EL－FIKY G S，KATO T.Continuous Distribution of the Horizontal Strain in the Tohoku District，Japan，Predicted by Least－squares Collocation［J］.Journal of Geodynamics，1999，27（2）：213－236.

［5］ WU J C，TANG H W，CHEN Y Q.The Current Strain Distribution in the North China Basin of Eastern China by Least－square Collocation［J］.Journal of Geodynamics，2006，41（5）：462－470.

［6］ HOLLENSTEIN C，MULLER M D，GEIGER A，et al.Crustal Motion and Deformation in Greece from a Decade of GPS Measurements，1993－2003［J］.Tectonophysics，2008，449（1）：17－40.

［7］ KAHLE H G，MULLER M V，GEIGER A，et al.The Strain Field in Northwestern Greece and the Ionian Islands：Results Inferred from GPS Measurements［J］.Tectonophysics，1995，249（1）：41－52.

［8］ KAHLE H G，COCARD M，PETER Y，et al.GPS－derived Strain Rate Field within the Boundary Zones of the Eurasian，African and Arabian Plates［J］.Journal Geophysical Research，2000，105（10）：23353－23370.

［9］ JIANG Zaisen，MA Zongjin，ZHANG Xi，et al.Horizontal Strain Field and Tectonic Deformation of China Mainland Revealed by Preliminary GPS Result［J］.Journal of Geodesy and Geodynamics，2003，46（3）：353－358.（江在森，马宗晋，张希，等.GPS初步结果揭示中国大陆水平应变场与构造变形［J］.地球物理学报，2003，46（3）：353－358.）

［10］ EGLI R，GEIGER A，WIGET A，et al.A Modified Least－squares Collocation Method for the Determination of Crustal Deformation：First Results in the Swiss Alps［J］.Geophysical Journal International，2007，168（1）：1－12.

［11］ YANG Yuanxi.Robust Estimation Theory and Its Applications［M］.Beijing：Bayi Publishing House，1993.（杨元喜.抗差估计理论及其应用［M］.北京：八一出版社，1993.）

［12］ YANG Yuanxi.Adaptively Robust Least Squares Estimation［J］.Acta Geodaetica et Cartographica Sinica，1996，25（3）：206－211.（杨元喜.自适应抗差最小二乘估计［J］.测绘学报，1996，25（3）：206－211.）

［13］ OU Jikun.Quasi－accurate Detection of Gross Errors（QUAD）［J］.Acta Geodaetica et Cartographica Sinica，1999，28（1）：15－20.（欧吉坤.粗差的拟准检定法（QUAD法）［J］.测绘学报，1999，28（1）：15－20.）

［14］ YANG Y X.Robust Estimation of Geodetic Datum Transformation［J］.Journal of Geodesy，1999，73（5）：268－274.

［15］ YANG Y，CHENG M K，SHUM C K，et al.Robust Estimation of Systematic Errors of Satellite Laser Range［J］.Journal of Geodesy，1999，76（6）：345－349.

［16］ ZHOU Jiangwen.Collocation by Two Variant Methods［J］.Acta Geodaetica et Cartographica Sinica，1981，10（1）：9－12.（周江文.拟合推估的两种解法［J］.测绘学报，1981，10（1）：9－12.）

［17］ YANG Y X.Robustfying Collocation［J］.Manuscripta Geodaetica，1992，17（1）：21－28.

［18］ WANG Rongxin.Mathematical Statistics［M］.Xi’an：Xi’an Jiaotong University Press，1986.（汪荣鑫.数理统计［M］.西安：西安交通大学出版社，1986.）

［19］ GUO Shunmin，JIANG Zaisen，ZHANG Chongli.Division and Motion Status of Blocks for the Northeastern Tibetan Plateau in Late Quaternary［J］.Seismology and Geology，2009，22（3）：219－231.（虢顺民，江在森，张崇立.青藏高原东北缘晚第四纪块体划分与运动态势研究［J］.地震地质，2009，22（3）：219－231.）