基于四要素的机械零部件失效率计算模型

王 正

中国北方发动机研究所柴油机高增压技术国防重点实验室,大同,037036

基于四要素的机械零部件失效率计算模型

王 正

中国北方发动机研究所柴油机高增压技术国防重点实验室,大同,037036

分析了影响典型失效率曲线变化的因素,提出了零部件失效率计算的四要素,即载荷、强度、强度退化规律以及寿命指标(载荷作用次数或时间)。分别在以载荷作用次数和时间为寿命度量指标框架下,建立了能够全面地体现载荷、强度、强度退化规律以及寿命指标等参数影响的零部件失效率计算四要素模型,并研究了零部件可靠度与失效率随寿命指标的变化规律。研究表明,零部件的可靠度随寿命指标的增大而逐渐减小,零部件的失效率随寿命指标变化具有浴盆曲线全部(或部分)特征。对于不同的强度分布、载荷分布和强度退化规律组合,零部件具有不同的可靠度,失效率曲线具有不同的形状。所建立的失效率模型无需依赖产品的失效数据信息,而只要在载荷、强度、强度退化规律以及寿命指标等参数已知的情况下便可以准确地计算零部件的失效率,可更好地在设计阶段指导零部件的可靠性设计。

失效率;载荷;强度;强度退化;寿命指标;零部件可靠性

0 引言

失效率作为机械产品可靠性的重要度量指标之一,常用于机械系统和装备的可靠性评价与维修管理。多年来,国内外学者从不同的角度对失效率进行了研究[1-9]。Xie等[3]研究了适用于具有浴盆形状失效率寿命数据的分布模型,该模型包括3个参数且可与指数分布和威布尔分布相联系。Zhang等[4]研究了运用软件可靠性增长模型分析系统测试数据和使用数据的现场失效率预测方法。Xue等[5]针对步进应力加速寿命试验提出了常应力下威布尔分布损伤失效率模型的参数估计方法。Toscano等[6]针对运行环境的变化提出了能够实时预测系统可靠性的动态失效率模型。Zafiropoulos等[7]考虑失效率的不确定性,提出了基于可靠度和费用的电子设备优化计算方法。Avinadav等[8]针对与人因相关的风险事件,提出了新的浴盆型故障函数。王学敏等[9]针对评估和统计数据的不确定性问题,利用概率生成函数,提出了根据权值来获得系统共因失效率的计算方法。

然而,现有的这些失效率计算方法大多采用统计的方法,即通过对产品实验数据和使用数据进行统计分析获得相应的寿命分布函数,进而得到失效率的表达式。显然,这种失效率计算方法很难在新产品的设计阶段对产品的失效率进行预计和指导产品的可靠性设计,特别是对于实验费用又高、样本量小的机械产品,在相对短的研制周期内很难甚至无法获得足够的产品失效数据[10]。

本文基于载荷与强度是影响产品失效率最基本因素的认识,研究零部件失效率在不同阶段变化的关键影响因素,提出决定零部件失效率的四要素,研究不需要依赖产品失效数据信息的零部件失效率计算方法,并建立基于四要素法的机械零部件失效率计算模型。

1 零部件失效率变化的影响因素分析

失效率作为一种能够适时描述产品可靠性的度量指标,可以直观地反映零部件或系统在任意时刻失效的可能情况。

如图1所示,典型的产品失效率曲线(即浴盆曲线)具有明显的“早期失效期(图1中的 A)”、“偶然失效期(图1中的B)”和“耗损失效期(图1中的C)”3个阶段的特征,但并不是所有的产品失效率曲线都具有浴盆曲线的全部特征。

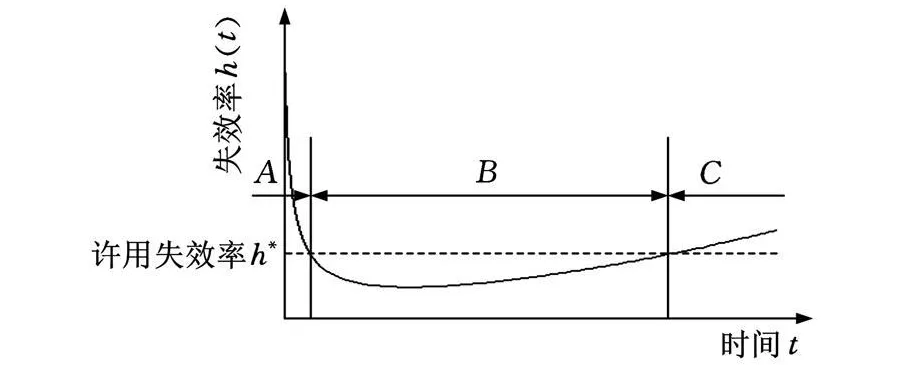
图1 典型的产品失效率曲线(浴盆曲线)

从内外因相互作用的观点看,产品失效率变化实质上反映的是产品所受载荷与其强度之间相对大小关系的概率特征随寿命指标的变化。在浴盆曲线中的早期失效期,产品的失效率随着使用时间的增加较快地下降。在这个时期,产品强度退化可以忽略,产品失效率主要是由于设计、制造、工艺缺陷等原因引起的强度不确定性与载荷不确定性共同决定的[11-12]。在浴盆曲线中的偶然失效期,产品的失效率很低且在数值上变化很小,产品在这一阶段的失效往往是由于偶然的原因所引起。此时,强度的不确定性对失效率的影响相对较小,而载荷的不确定性对失效率的影响却相对较大。在浴盆曲线中的耗损失效期,失效率随寿命指标的增大而逐渐上升。这一阶段的失效主要是由于强度的退化(如磨损、疲劳、老化等)所引起。

从对产品失效率变化影响因素的分析我们可以看出,决定失效率的要素可以总结为:载荷、强度、强度退化规律以及寿命指标(时间或载荷作用次数)等。只要给定这4个要素的相关参数,原则上便可以确定产品的失效率。

2 零部件失效率计算的四要素模型

零部件在实际使用中,既有以载荷作用次数作为其寿命度量指标的,也有以工作时间作为其寿命度量指标的。下面,针对单一失效模式零部件,分别以载荷作用次数和时间为寿命度量指标,建立基于载荷、强度、强度退化规律以及寿命指标等四要素的机械零部件失效率计算模型。

2.1 以载荷作用次数为寿命指标的零部件失效率

传统的直接运用载荷-强度干涉理论建立的零部件可靠性模型并不能很好地反映零部件可靠度随载荷作用次数的变化规律。用这些模型计算得到的可靠度实际上是随机载荷作用一次或特定次数的可靠度[13-15],严格地讲,是一个静态的可靠度[11,16]。因此,也无法基于这样的可靠性模型得到零部件的失效率表达式。

机械产品大多数失效模式(如疲劳、磨损、腐蚀等)所对应的强度指标会随着载荷作用次数的增加而逐步降低,即剩余强度在不断地发生变化。通常,强度退化规律与载荷幅值、载荷作用次数以及载荷作用顺序有关。在载荷幅值不变或变化幅度相对较小的情况下,可以认为剩余强度取决于初始强度、载荷均值以及载荷作用次数[17]。此时,剩余强度可表示为初始强度与载荷作用次数的函数。

以载荷作用次数为寿命度量指标时,载荷的不确定性可以用概率分布函数描述。设载荷的概率密度函数和累积分布函数分别为 fs(s)和Fs(s)。当零件的初始强度为确定值δ时,零件在经历载荷作用n次后的强度δ(n)也为确定的值。用An表示零件在随机载荷作用第n次时不发生失效,显然,An事件发生的概率可表示为

进一步,当零件经历的总载荷作用次数相对较大时,零件的失效率可表示为[15]

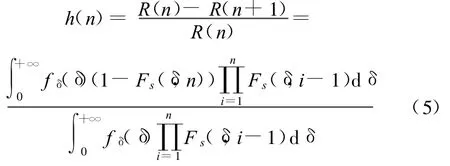
在式(5)所示的零件失效率模型中,只需已知零部件的强度与载荷概率分布、强度退化规律以及载荷作用次数,便可以计算出零件的失效率,而无需依赖大量的实验数据和使用数据。

2.2 以时间为寿命指标时的零部件失效率

以时间为寿命度量指标时,产品在t时刻的失效率h(t)与可靠度R(t)的关系可表示为

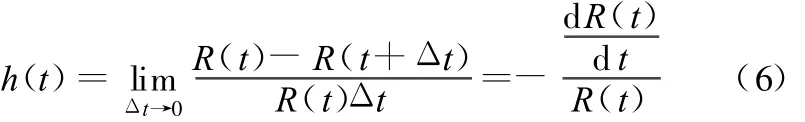
当零部件以时间作为其寿命度量指标时,载荷一般都具有时间维和幅度维的不确定特征,即载荷出现时间的不确定性和载荷出现时幅值大小的不确定性。在这里,采用随机载荷的二维描述法来刻画载荷的不确定性特征[11,18],即用参数为λ(t)的泊松随机过程来描述载荷作用次数随时间变化的不确定性特征,用概率分布函数(其概率密度函数和累积分布函数分别为 fs(s)和Fs(s))来描述载荷在幅度维的不确定性特征。同时,当零部件在t时刻的强度取决于其初始强度和时间t时,强度退化规律可表示为初始强度与时间t的函数。

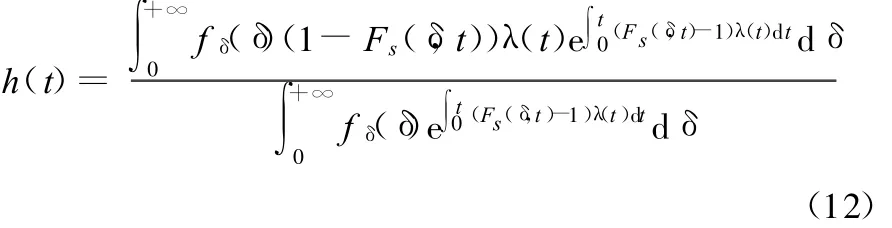
式(12)所示的零件失效率计算模型能够全面体现载荷、强度、强度退化以及时间等参数对零件失效率的影响。同样,只需要知道零件的强度与载荷概率分布、强度的退化规律以及时间,便可运用式(12)准确地计算出零件的失效率。

3 零部件失效率变化规律研究

下面分别以载荷作用次数和时间为寿命度量指标,运用式(4)和式(5)、式(11)和式(12)所示的零件可靠度与失效率计算四要素模型,在零件强度、载荷以及强度退化规律已知的情况下,以零件强度和载荷幅值均服从正态分布为例,研究零部件可靠度与失效率随寿命指标的变化规律。

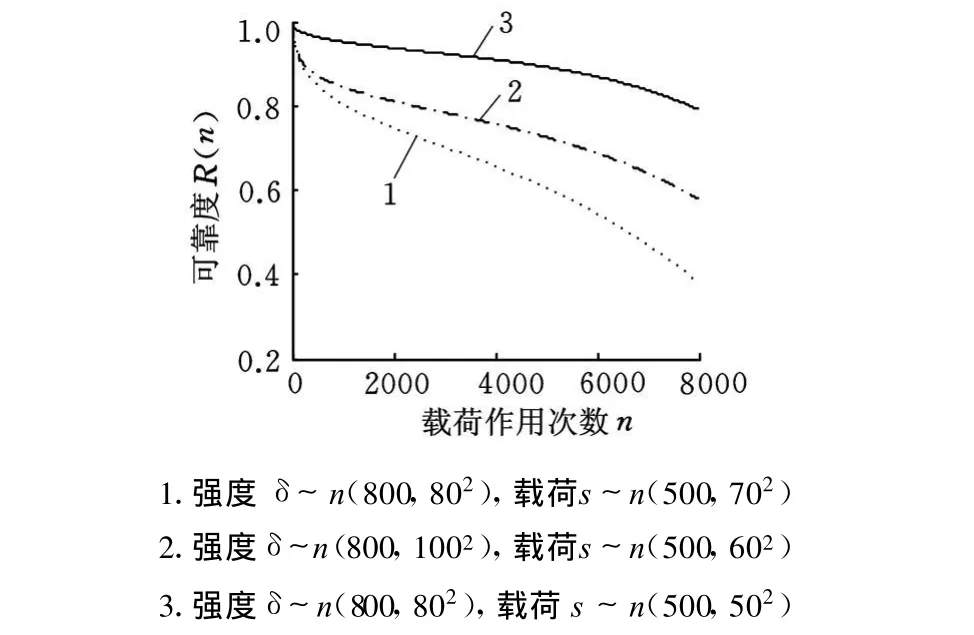
图2 零件可靠度随载荷作用次数的变化

图3 零件失效率随载荷作用次数的变化

以时间为寿命度量指标时,强度退化规律为δ(t)=δe(-0.00002t),载荷作用过程服从参数为λ(t)=0.5h-1的泊松随机过程,载荷幅值与强度的分布参数分为三种情况,分别如图 4、图5所示。

从图2和图4可以看出,在强度、载荷、强度退化规律以及寿命指标已知的情况下,可以运用本文模型准确地计算零部件的可靠度,科学地反映零部件可靠度随寿命指标的变化规律。对于不同的强度分布参数、载荷分布参数以及强度退化规律,零部件可靠度随寿命指标的变化也不同。

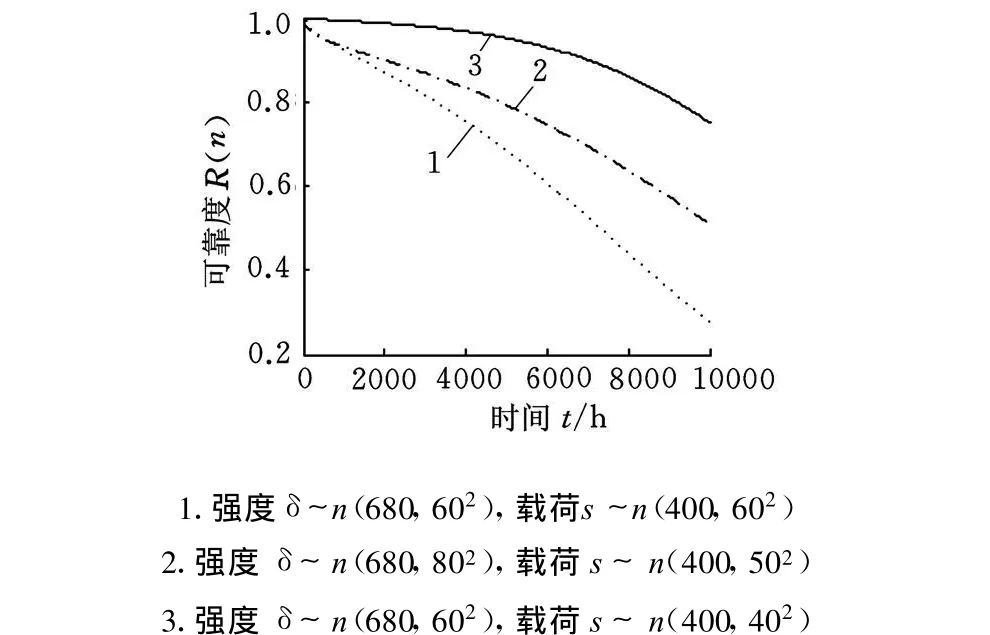
图4 零件可靠度随时间的变化

从图3和图5可以看出,在强度、载荷、强度退化规律以及寿命指标等4个要素已知的情况下,可以运用本文模型准确地计算零部件的失效率。对于不同的强度分布参数、载荷分布参数以及强度退化规律组合,零部件的失效率随寿命指标的变化规律也不同。同时,还可以看出零部件的失效率随寿命指标的变化规律具有浴盆曲线全部(或部分)的特征,这与通过对产品失效数据进行统计分析得出的失效率变化规律是相吻合的。

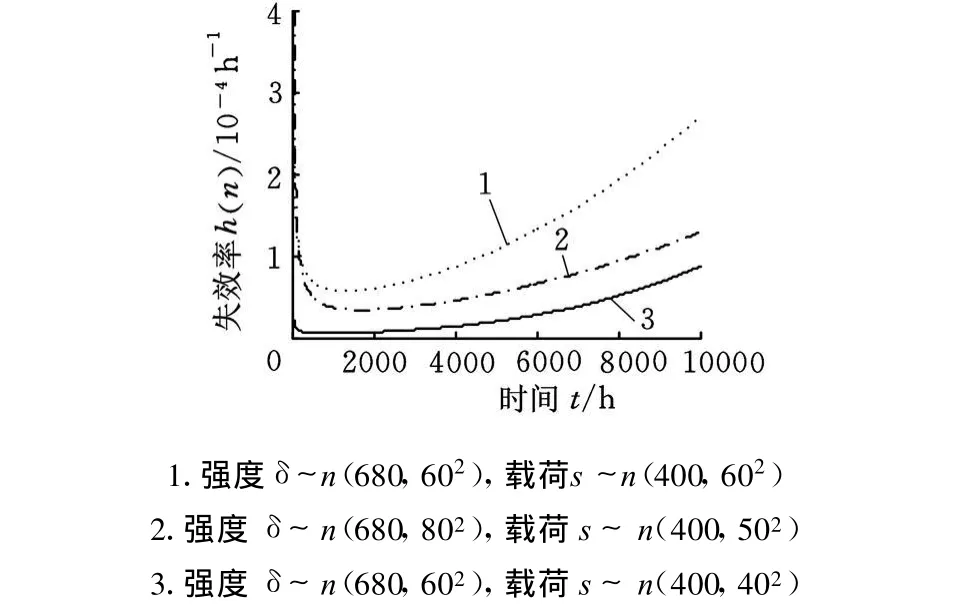
图5 零件失效率随时间的变化

4 结论

本文分析了零部件失效率变化的影响因素,提出了决定机械零部件失效率的四要素,即载荷、强度、强度退化规律和寿命指标。在此基础上,分别以载荷作用次数和时间为寿命度量指标,建立了机械零部件可靠度与失效率计算的四要素模型,并研究了零部件可靠度与失效率随寿命指标的变化规律。研究表明,在载荷、强度、强度退化规律以及寿命指标参数已知的情况下,可以运用本文建立的四要素模型准确地计算零部件的可靠度与失效率,科学地反映零部件可靠度与失效率随寿命指标的变化规律。对于不同强度分布参数、载荷分布参数以及强度退化规律的组合,零部件可靠度与失效率随寿命指标的变化规律也不同。同时,零部件的可靠度随寿命指标在逐渐减小,失效率随寿命指标的变化具有浴盆曲线全部(或部分)的特征。这一结论与通过对产品失效数据进行统计分析得出的失效率变化规律是相吻合的。

本文所建立的机械零部件失效率四要素计算模型能够科学地体现载荷、强度、强度退化规律以及寿命指标对零部件失效率的影响,且在计算过程中无需依赖产品的失效数据。因此,在产品的设计阶段,就能够根据零部件的相关参数准确地对零部件进行可靠性分析与失效率计算,可以更好地指导机械零部件的可靠性设计。

[1] Bow les J B.Commentary-caution:Constant Failurerate ModelsMay be Hazardous to Your Design[J].IEEE T ransactions on Reliability,2002,51(3):375-377.

[2] H jorth U.A Reliability Distribution with Increasing,Decreasing,Constant and Bathtub-shaped Failure Rates[J].Technometrics,1980,22(1):99-107.

[3] Xie M,Tang Y,Goh TN.A Modified Weibull Extension with Bathtub-shaped Failure Rate Function[J].Re liability Engineering and System Safety,2002,76(3):279-285.

[4] Zhang Xuemei,Pham H.So ftware Field Failure Rate Prediction before Softw are Deployment[J].The Journalof Systems and Softw are,2006,79(3):291-300.

[5] Xue Xiaoling,Fei Heliang.Parameter Estimation of the Weibu ll Distribution Tampered Failure Rate Model under a Normal Stress[J].Chinese Journal o f Applied Probability and Statistics,2004,20(2):126-132.

[6] Toscano R,Lyonnet P.On-line Reliability Prediction via Dynamic Failure Rate Model[J].IEEE T ransactions on Reliability,2008,57(3):452-457.

[7] Zafiropou los E P,Dialynas E N.Reliability and Cost Optimization of Electronic Devices Considering the Com ponent Failure Rate Uncertainty[J].Reliability Engineering and System Safety,2004,84(3):271-284.

[8] Avinadav T,Raz T.A New Inverted U-shape H azard Function[J].IEEE T ransactions on Reliability,2008,57(1):32-40.

[9] 王学敏,谢里阳,周金宇.共因失效率的不确定性评估[J].航空学报,2005,26(4):446-449.

[10] 王正.基于载荷-强度干涉的零件与系统失效率计算方法[R].北京:北京航空航天大学,2009.

[11] W ang Zheng,Xie Liyang.Dynam ic Reliability Model o f Components under Random Load[J].IEEE T ransactions on Reliability,2008,57(3):474-479.

[12] 王正,谢里阳.零件动态可靠性建模及早期失效率研究[J].航空学报,2007,28(6):1378-1382.

[13] 张义民.任意分布参数的机械零件的可靠性灵敏度设计[J].机械工程学报,2004,40(8):100-105.

[14] An Zongwen,Huang Hongzhong,Liu Yu.A Discrete Stress-strength Interference Model Based on Universal Generating Function[J].Reliability Engineering and System Safety,2008,93(10):1485-1490.

[15] 王正,康锐,谢里阳.以载荷作用次数为寿命度量指标的失效相关系统可靠性建模[J].机械工程学报,2010,46(6):188-194.

[16] Cazuguel M,Renaud C,Cognard J Y.Timevariant Re liability of Non linear Structures:Application to a Representative Part of a Plate Floor[J].Quality and Reliability Engineering International,2006,22(1):101-108.

[17] 周迅,俞小莉,李迎.弯曲疲劳载荷下曲轴剩余强度的简化试验模型[J].兵工学报,2006,27(4):712-715.

[18] 王正.零部件与系统动态可靠性建模理论与方法[D].沈阳:东北大学,2008.

Failure RateModelof Mechanical Components Based on Four Elements

Wang Zheng
National Key Laboratory of Diesel Engine Turbocharging Technology,China North Engine Research Institute,Datong,Shanxi,037036

The factors affecting the typical failure rate curve were analyzed,and four elements including load,strength,strength degradation and life index(namely,the number of load application and time)w ere proposed for calculating the failure rate of components.Taking the number of load app lication and time as the life index,respectively,the failure ratemodels of components consisting of four elementswere developed,which can embody the parameters of load,strength,strength degradation and life.Then,the behaviors of the reliability and failure rate of components changing as the life index were studied.The results show that the failure rate curvesof components have the partialorwhole characteristics of bathtub curve.For differentparametersof load,strength and the rule of strength degradation,the failure rate curves of components have different shapes.The models derived herein can calcu late the failure rate of components as long as the known parameters of load,strength and its degradation and life index,and can direct the reliability-based design of componentsmore scientifically.

failure rate;load;strength;strength degradation;life index;com ponent reliability

TB114.3;TH122

1004—132X(2011)12—1472—05

2010—08—05

国家自然科学基金资助项目(50905007);中国博士后科学基金资助项目(200902042);国防科技重点实验室基金资助项目(9140C3306131001)

(编辑 何成根)作者简介:王 正,男,1981年生。中国北方发动机研究所柴油机高增压技术国防重点实验室副研究员。主要研究方向为机械系统可靠性、柴油机可靠性技术、柴油机高增压技术、结构疲劳寿命预测。发表论文50余篇,出版专著1部。