工件几何模型对不锈钢切削力数值计算影响研究
2011-01-29胡于进王学林
姚 嵩 胡于进 王学林
华中科技大学,武汉,430074
工件几何模型对不锈钢切削力数值计算影响研究
姚 嵩 胡于进 王学林
华中科技大学,武汉,430074
通过研究AISI-316L材料动态本构关系、刀屑接触、切屑分离、切屑断裂等关键技术建立了正交切削有限元模型。运用大型通用有限元软件ABAQUS对切削加工过程进行模拟仿真,对不同工件几何模型下的模拟结果进行分析和验证,证明所建立的有限元模型是合理的,并通过实验结果比较得出优化的几何模型。
直角切削;几何建模;切削力;316L不锈钢
0 引言
切削力计算对切削机理的研究,对计算功率消耗,对刀具、机床、夹具的设计,对制定合理的切削用量,优化刀具几何参数,都具有非常重要的意义[1]。近年来随着计算机技术的飞速发展,数值模拟方法特别是有限元方法在切削模拟中的地位越来越明显。
Strenkow ski等[2]预先设置一条分离线来对切屑和工件的分离进行建模,Marusich等[3]使用显示积分算法和网格自适应策略对高速切削进行建模,Yang等[4]采用弹-刚性耦合有限元模型模拟高速切削过程。
当前所采用的切削力有限元计算都将工件简化为平直的,这使得计算模型的建立非常方便。但实际上,在车削等加工过程中,工件表面是回转面,而非平直的,因此,有必要对工件表面曲率对切削力的影响进行讨论。ABAQUS是功能强大的有限元分析软件,可以分析复杂的固体力学和结构力学系统,模拟非常庞大复杂的模型,处理高度非线性问题。
本文使用ABAQUS/Explict程序系统对切削加工过程进行模拟,ABAQUS/Exp lict程序系统可以从原理上处理切削加工过程这种很强的非线性问题,且能够定义复杂的接触条件,并利用动态显式热力耦合分析步对切削加工过程进行动态模拟。
本文研究了切削过程中所必需的关键技术,通过对比验证了模型结果的可靠性。讨论比较了AISI-316L奥氏体不锈钢切削过程中两种不同的几何模型对切削力和切屑形态的影响,预测了在不同切削用量下的切削力。最后验证了两个几何模型结果的准确性。
1 几何模型的提出和比较
金属的切削加工过程是一个复杂的非线性问题(材料非线性、边界非线性、几何非线性),无论是从理论上还是从实践上来看都是一个复杂的动态过程,材料模型既有弹性变形,又有塑性变形。
以前的研究人员主要是通过以下几种方法来提高切削过程的有限元模拟精度:①通过修改材料的本构模型,以更好地反映材料的特性;②通过改进工件材料的实验方法,获得更为精确的试样材料参数;③通过刀-屑摩擦模型的改进来提高有限元的模拟精度。
回转体几何模型和矩形几何模型如图1所示,试件的曲率半径较大时实验的误差较小,但在一般的切削机理性研究实验中所采用的试件曲率半径都不会很大,这样就会对预测结果产生一定的误差。
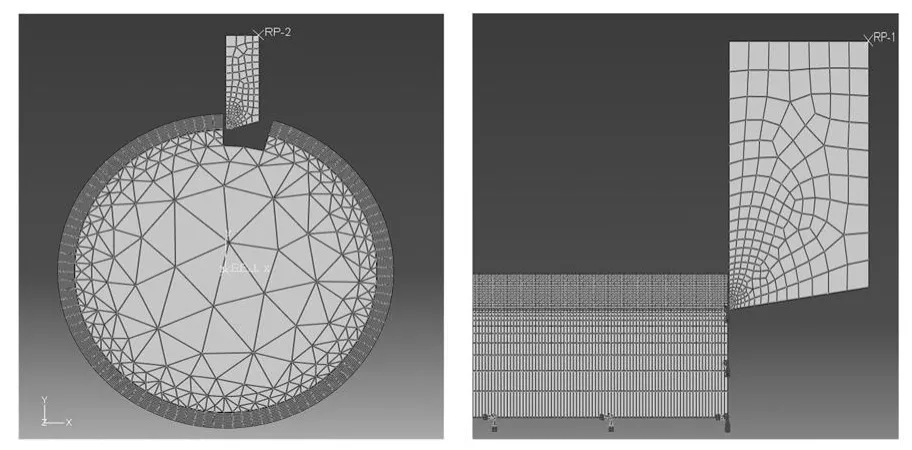
图1 回转体几何模型和矩形几何模型
本文将AISI-316L切削实验中实际的工件形状简化成回转体形状进行几何建模。在保证材料参数、接触条件、载荷约束等相同的情况下分别用两个模型进行模拟并与实验结果进行误差比较。
2 金属切削过程模拟的关键技术
2.1 有限元模型的建立
图1模型的工件材料为316L不锈钢,刀具材料为硬质合金,表1所示为工件材料和刀具材料的物理属性。模型在刀具表面和工件表面存在与空气的对流,对流系数为0.02W/(m2◦K);环境温度为20℃;研究中忽略了热辐射的影响。
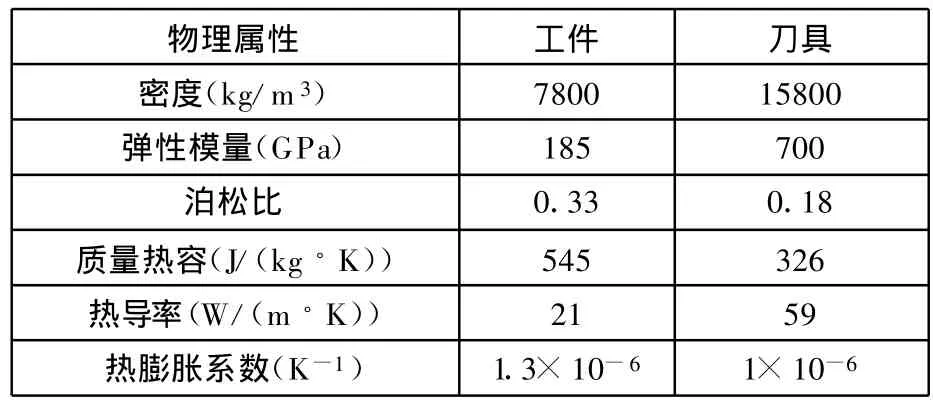
表1 AISI-316L钢及硬质合金刀具材料的物理属性[5]
本文选择的模型为动态热力耦合类型,切削层和工件使用 4节点双线性减缩积分单元(CPE4R)进行离散。采用加强型沙漏控制切削层单元。
在矩形模型的底部和未切削层左右各施加一个水平方向的约束,以限制工件底部的位移,使底部未加工层完全固定,失去所有的自由度,将刀具设置成刚体,并设定切削速度。
回转体模型是把工件中心的一小部分定义为刚体,施加的角速度等价于带动工件旋转的实验转速,将刀具设置成刚体,并约束所有的自由度,使回转体固定不动。
2.2 Johnson-Cook材料本构关系
在金属材料切削加工中存在三种效应,分别为应变硬化效应、应变率强化效应和热软化效应。应变硬化效应表征材料的流动应力随着应变的增加而增大,应变率强化效应表征材料的流动应力随着应变率的增加而增大,热软化效应表征材料的流动应力随着温度的增加而减小。Johnson-Cook模型引入了表征以上三种效应的参数,能够反映出大应变、大应变率和高温情况下的金属本构行为,适合于不同的材料参数而且形式较为简单,因此本文采用该模型来描述金属的材料特性。表2所示为AISI-316L钢的Johnson-Cook材料参数。

表2 AISI-316L钢的Johnson-Cook材料参数
Johnson-Cook[6]模型可表示为

式(1)只涉及流动应力,因而它不适用于Johnson-Cook模型中材料的断裂失效,因为Johnson-Cook模型中材料的断裂是以等效塑性应变来衡量的,因此本构模型的动态失效准则可表示为
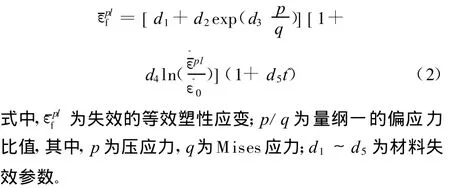
2.3 切屑分离准则
一个合理的分离准则只有真实地反映切削加工材料的力学和物理性质,才能得到合理的结果。到目前为止,在有限元模拟中已经提出了各种切屑分离准则,这些准则可以分为几何准则和物理准则两种类型。
几何准则主要通过变形体几何尺寸的变化来判断分离与否。物理准则主要是基于制定的一些物理量的值是否达到了临界值而建立的,主要物理准则有基于等效塑性应变准则、基于应变能量密度准则、断裂应力准则等。
为了能够更加真实地反映模拟结果,本文采用ABAQUS/Exp lict中一个动态的失效模型来模拟高速切削过程中切屑同工件的分离过程,属于物理分离准则。
Johnson-Cook模型的断裂标准衡量参数w定义为

2.4 接触摩擦模型
在金属切削加工过程中,刀具的前刀面对切屑以及刀具的后刀面和工件已加工表面都存在摩擦和挤压作用。同时,在切屑、刀具和工件中引起温度、应力和应变等物理量的重新分布,这些物理量之间的相互耦合作用使工件产生塑性变形。因此,正确处理前刀面的接触摩擦问题,建立刀具与工件之间合理的摩擦模型是切削加工模拟成功实现的关键因素。图2所示为沿刀屑界面的理想应力分布模型[7]。
切削过程中的摩擦产生于两个位置:一个是刀具和切屑的接触面,即刀-屑区;另一个是刀具和工件表面的接触区,即刀-工件区。这些区域的正压力都很高,金属材料性能受到高温大变形的影响而发生改变。这些区域的应力因存在滑动区和黏结区,所以分布是不均匀的。在滑动区,由于正应力小所以摩擦较小,属于外摩擦,而在黏结区,由于接触区的高温高压作用,致使金属内部出现剪切滑移,即内摩擦,内摩擦与材料的流动应力特性以及黏结面积大小有关,所以其变化规律与外摩擦不同。本文基于Coulomb[8]摩擦定律而建立的模型为
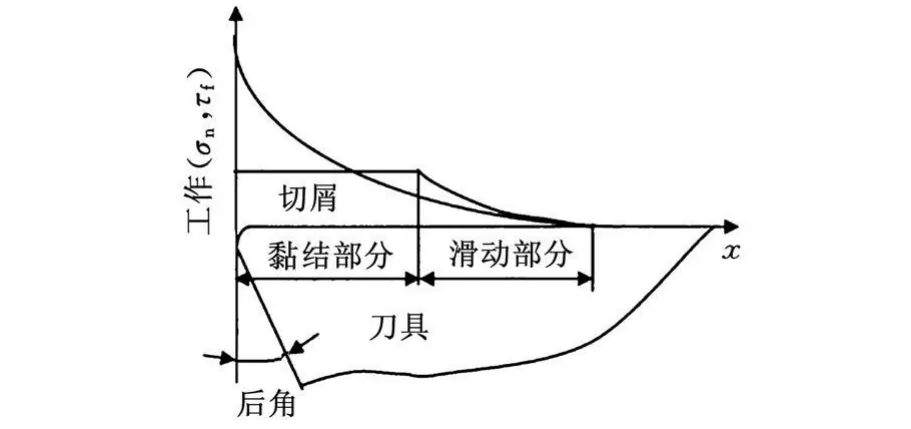
图2 沿刀屑界面的理想应力分布模型

3 实验模型准确性验证
表3所示为Umbrello等[9]的实验结果与本文模拟结果比较。采用Johnson-Cook模型的5个不同的材料本构模型(编号分别为M 1、M 2、M 3、M 4、M 5)模拟结果去和实验数据进行比较,结果见表3。为了验证本文切削模型的准确性,也按照相同的条件用矩形模型模拟出一组数据。实验采用的参数为:前角 γ0=0°,切削速度v=100m/m in,进给量ap=0.2mm/r,切削宽度b=6mm。
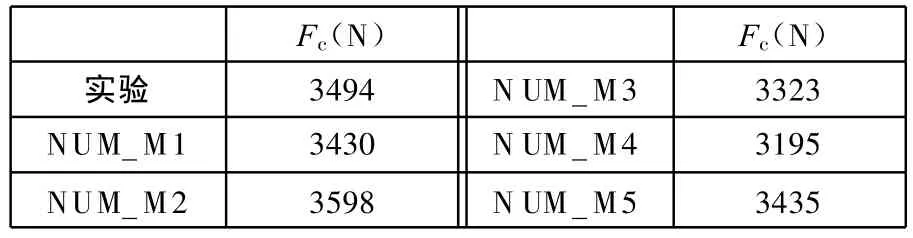
表3 Umbrello等[9]的实验结果与模拟结果比较
图3所示为切削过程中切削力随时间的变化关系。取进入稳态过程后的切削力的平均值为模型预测的切削力,从图3可以看出,在进入稳态切削后切削力曲线基本在3.5kN上下波动,与文献[9]中的实验数据较接近。
4 结果分析与讨论
本文不同几何模型的预测结果与 Tounsi等[10]的实验结果数据见表4、表5。切削实验参数为:前角 γ0=0°,切削速度 v=(67.2,128.4,187.2)m/m in,进给量 ap=(0.1,0.2,0.3)mm/r,切削宽度b=2mm。
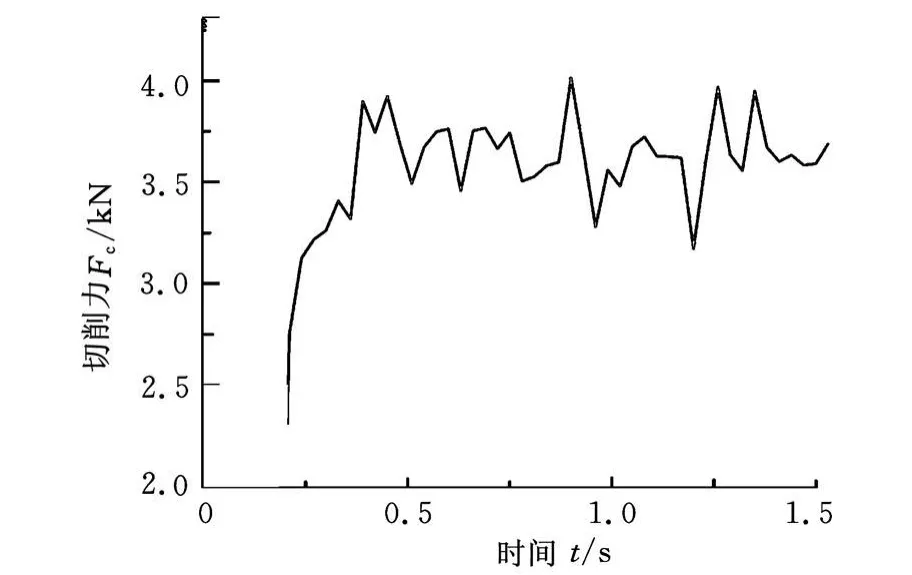
图3 模型预测的切削力随时间变化的关系图
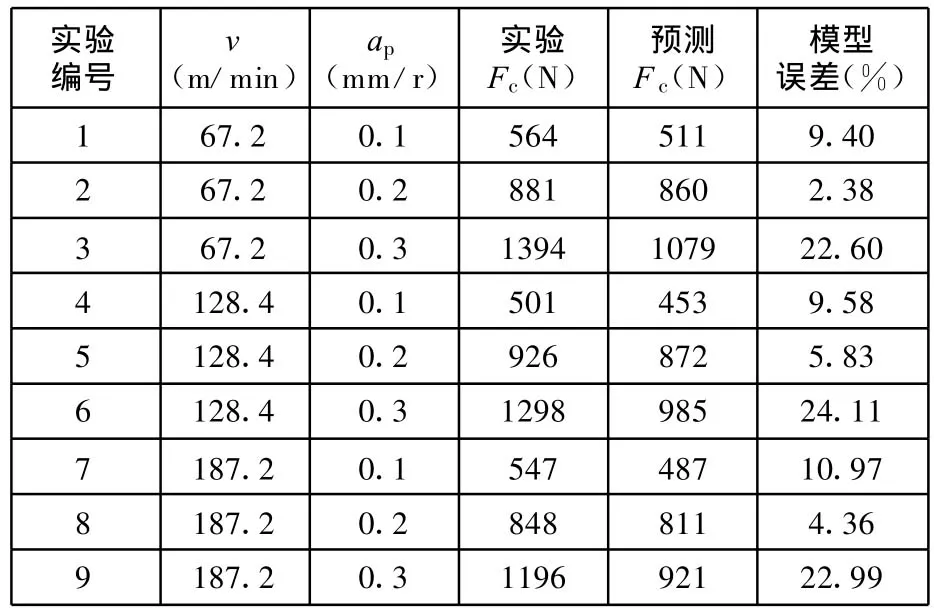
表4 矩形模型预测数据与实验数据比较
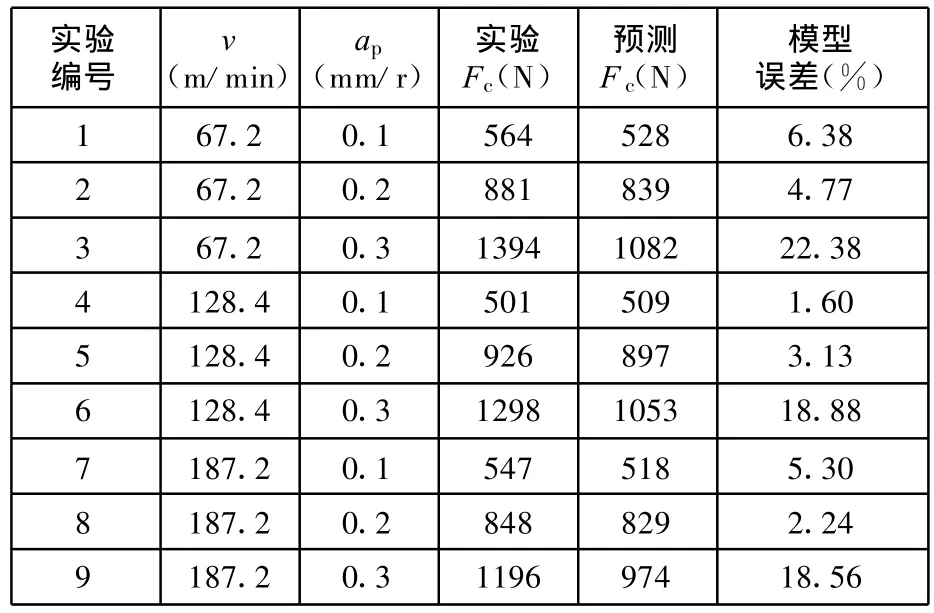
表5 回转体模型预测数据与实验数据比较
图4所示为两组模型切削力实验结果与预测结果的比较。
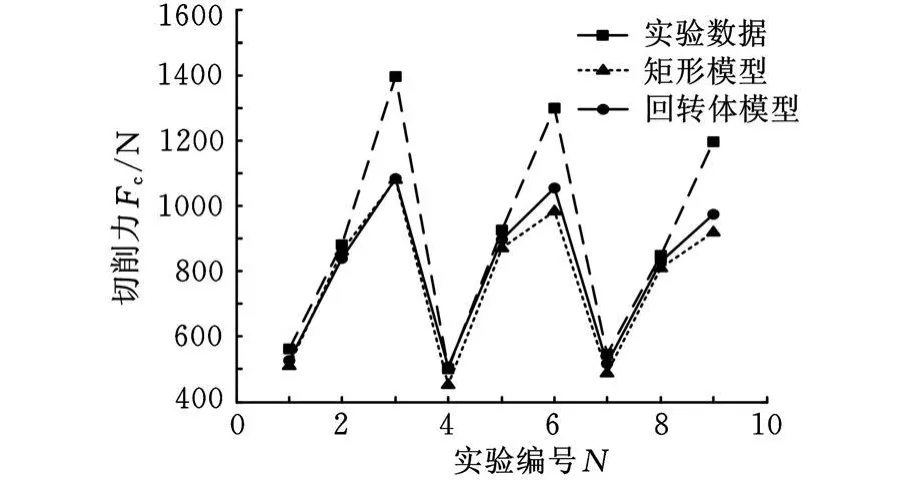
图4 切削力的实验与预测结果
取实验编号为2的实验结果进行分析,其v=67.2m/min,a p=0.2mm/r的两个模型的模拟结果如图5~图10所示。
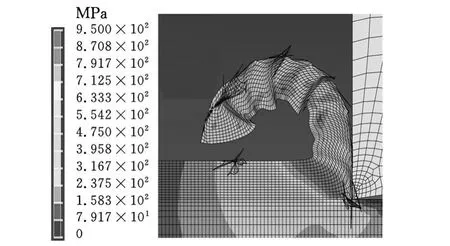
图5 平面模型m ises应力分布

图6 回转体模型m ises应力分布
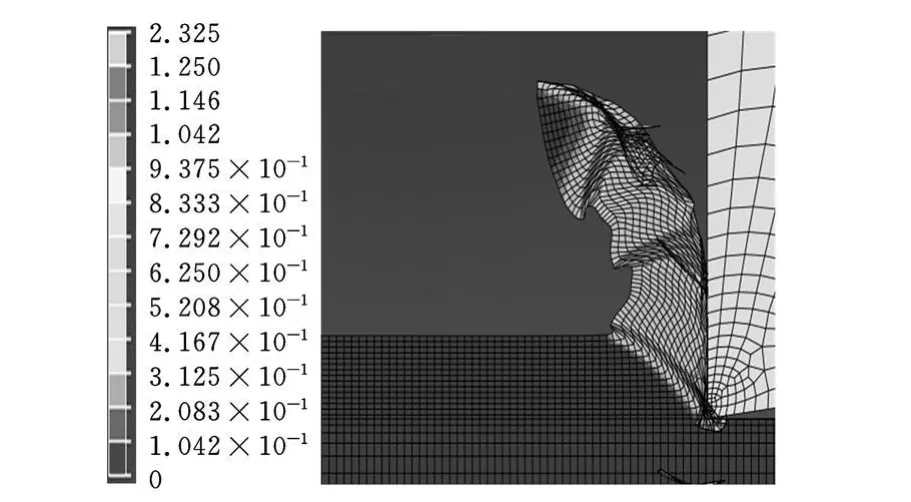
图7 平面模型塑性应变分布
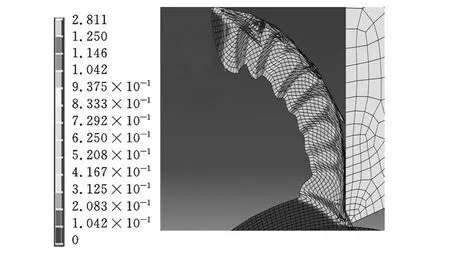
图8 回转体模型塑性应变分布
(1)通过表4和表5中2个几何模型所测数据与实验所得数据的比较可知,矩形模型和回转体模型相对于实验的平均偏差分别为12.47%、9.25%,可以看出2个模型的预测数据都能很好地贴合实验结果,验证了本文模型模拟AISI-316L不锈钢的切削过程的正确性和预测切削参数的准确性。同时回转体几何模型的结果精度要更准确一些。
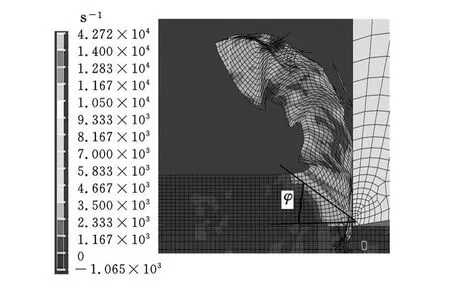
图9 平面模型应变率分布
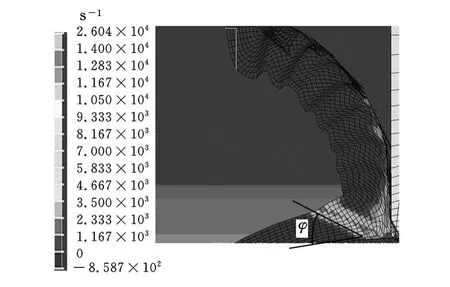
图10 回转体模型应变率分布
(2)比较表4和表5实验数据与预测数据可以发现:在同一切削厚度情况下,一定范围内切削速度的变化对切削精度的影响并不大,切削层厚度对切削精度的影响是主要的,同一速度条件下预测的精度误差会随着切削层厚度的增大而增大。这主要是由于切削层网格没有很好地细化以及切削层自接触等因素造成的,可通过进一步优化网格提高精度。
(3)对比图5、图 6和图7、图 8可以看出:回转体模型云图的最大应力与应变的幅值都要大于矩形模型的最大应力与应变的幅值。对比图9、图10可以看出:回转体模型的剪切角要小于矩形模型的剪切角。实验证明,剪切角的大小与切削力的大小有直接联系,对于同一工件材料,当剪切角较大时,剪切面积变小,切削比较省力,所测得的切削力较小。另外,通过图5~图10对比可以发现:回转体的切屑形状更符合实验加工所得的切屑形状。
5 结束语
本文在已验证过的切削模型的基础上,比较在相同条件下,同一工件不同的形状的几何建模所预测的切削力及应力和应变的分布。从结果可以看出:几何模型越贴近于实际工件的形状所预测的切削力的结果和其他切削参数的分布就更接近于实际的实验数据。所以在进行切削力、残余应力等机理性研究时,在没有明显增加模型的复杂程度的情况下,改进模型的几何形状可以一定程度地提高预测数据的准确性。
[1] 陈日曜.金属切削原理[M].北京:机械工业出版社,1993.
[2] Strenkow ski I S,Carrol III I T.A Finite Element Model o f O rthogonal Metal Cutting[J].Trans ASME J.Eng.Ind,1985,107:349-354.
[3] Manusich T D,O rtiz M.Modeling and Simulation of H igh Speed Machining[J].Int.J.Numer Methods Engrg.,1995,38:3675-3694.
[4] Yang Z,Sad ler JP.On Issues of Elastic-rigid Coupling in Finite ElementModeling of H igh Speed Machines[J].Mechanism and Machine Theory,2000,35:71-82.
[5] Bonnet C,Valiorgue F,Rech J,etal.Developmento f a Friction Modelling Method in Dry Cutting of A ISI 316Laustenitic Stain less Steel[J].International Journal of Material Form ing,2008(S1):1211-1214.
[6] Johnson G R,Cook W H.A Construetive Model and Data for Metals Sub jected to Large Strains,H igh Strain Rates and H igh Temperatures[J].Proceedings of the Seventh Intenational Symposium on Ballisties,1983,28:541,28-547.
[7] Ng E G,Aspinw all D K,Brazil D,et al.Modelling of Temperature and Forces When O rthogonally Machining Hardened Steel[J].International Journa l o f Machine Tools&Manufacture,1999,39:885-903.
[8] Wu Jungshu,Dillon O W,Lu W Y.Thermo-viscoplastic Modeling Process Using a M ixed Finite Elment Method[J].Journal of Manu factureing Science and Engineering,1996,118(4):470-482.
[9] Umbrello D,Saoubi R M,Outeiro JC.The Influence of Johnson-cook Material Constants on Finite Element Simulation of Machining of AISI 316L Steel[J].International Journalof Machine Tools&Manufacture,2007,47:462-470.
[10] Tounsi N,Vincenti J,Otho A,et al.From the Basics of O rthogonalMetal Cutting Toward the Indentification o f the Constitutive Equation[J].International Journal of Machine Tools and Manufacturing,2002,42(2):1373-1383.
Influence of Workpiece Geometry on Numerical Calculation of Cutting Force for Stainless Steel
Yao Song H u Yu jin Wang Xuelin
Huazhong University of Science and Technology,Wuhan,430074
This paper is to establish a finite elementmodel of orthogonal cutting by studying the key technology of dynam ic constitutive relation o f A ISI-316L materials,contacts between too l and chip,chip separation,chip crack.Authorsused large-scale finite element software ABAQUS to simulate the cutting process,then discussed and compared the simulation results in different geometric models.Finally it is indicated that the estab lished finite elementm odel is reasonab le,and an op timal geometricmodel is obtained from experiments.
orthogonalm etal cutting;geometricmodeling;cutting force;316L stainless steel
TG506.71
1004—132X(2011)12—1392—05
2010—08—06
国家重大基础研究发展计划(973计划)资助项目(2009CB724306)
(编辑 何成根)
姚 嵩,男,1986年生。华中科技大学机械科学与工程学院硕士研究生。主要研究方向为金属切削有限元分析。胡于进,男,1958年生。华中科技大学机械科学与工程学院教授、博士研究生导师。王学林,男,1963年生。华中科技大学机械科学与工程学院教授、博士研究生导师。
