电磁跟踪方法的研究进展

【作 者】葛鑫，邬小玫，汪源源，方祖祥

电磁跟踪（electromagnetic tracking），亦称磁场定位，是一种利用磁场获得物体位置和空间姿态的方法。可广泛应用于瞄准、运动跟踪、介入手术导航、自由臂三维超声成像等诸多领域。相比于其他空间定位方法，电磁跟踪具有无损伤、三维、无视线问题、操作简便等优点，但也有易受环境中金属及铁磁性物质干扰的缺点。最早的电磁跟踪方法包括1975年J.Kuipers提出的方法[1]和1977年F.H.Raab提出的方法[2]。之后的三十年，研究人员围绕提高精度和降低干扰（如金属导致的磁场扭曲等）两个主要问题，提出了多种电磁跟踪的方法、并在跟踪和校准算法、干扰抑制和消除等方面做了一系列工作，使得电磁跟踪技术有了长足的进展。本文对电磁跟踪方法发展过程中的主要方法进行了归类和总结，并就跟踪算法、校准方法两个关键问题进行了探讨。

1 电磁跟踪方法

一个基本的电磁跟踪系统一般由以下几部分构成：磁场源、磁传感器、计算和控制单元（如PC机）。在基本单元一致的前提下，不同跟踪方法的区别主要体现以下几点：磁场激励方式（AC、DC等）、磁场源和传感器的数量、配置方式（平面、正交）和几何形状等方面[3]。

1.1 磁场激励方式

在磁场激励方式方面，目前主要有交流（AC）磁场、脉冲直流磁场（Pulsed DC）两种方式。

早期的电磁跟踪方法一般采用交流磁场[1-2]，也称之为第一代电磁跟踪方法[4]。采用线圈作为传感器，故只能测量交流磁场。当环境中存在金属时，交变的磁场会在金属内部感应出涡流，进而产生干扰磁场，影响系统的测量精度。涡流干扰是困扰交流电磁跟踪技术的一个主要难题。

脉冲直流磁场的方法最早由Blood等人提出[5]，旨在解决环境金属造成的涡流干扰等问题，也称为第二代电磁跟踪方法[4]。由于采用直流的激励方式，在脉冲边沿之后经过的稳定一定时间，磁场不再变化，不再感应出涡流。此外，采用脉冲直流的方式，利用相邻的有磁场激励的时间段和无磁场激励的时间段测量的结果之差，可以较好的抵消地磁场和环境中铁磁性物质等造成的准静态干扰的影响。由于以上的优势，脉冲直流的电磁跟踪方法得到了较为广泛的应用。

除此之外，还有采用永磁体作为磁场源[15]的 。其特点是不需要外加激励，体内部分不需要配备很长的导线与体外激励装置。永磁体也不易形成涡流干扰。但是，环境中铁磁性物质的对永磁体产生的磁场有较大干扰。

1.2 磁场源和传 感器的数量、配置方式

在磁场源和传感器的数量配置方面，研究人员提出了许多种方法，其中典型的方法如表1所示。

1975-1977年，Kuipers等人[1,6]采用正交传感器和磁场源的二维三自由度和三维五自由度的磁场跟踪方法。1977年，Raab等人在此基础上提出了采用正交的三轴线圈作为磁场源[2,7]，正交的三轴线圈作为磁传感器的基于AC磁场的六自由度电磁跟踪方法，他们在Kuipers的方法的基础上进行了细致的分析，采用无限远磁偶极子模型（infinitesimal magnetic dipole model），提出了基于旋转变换的算法。此后，这种磁场配置方式成为电磁跟踪领域的主流配置方式，众多研究人员沿用了这一配置方式，再次进行激励方式、算法和抗干扰等各方面的改进。例如，1989年，Blood等人[5]采用相同的配置方式提出了基于脉冲直流磁场的三维电磁跟踪方法。

类似的，对正交磁场源或磁传感器的轴数进行修改，提出了一些其他的磁场配置方式。1982年，Raab[8]等人在之前方法的基础上将磁传感器减少为二维，实现了五自由度的电磁跟踪。由于两轴的磁场传感器更加易于缩小体积，而在一些应用中五自由度也可以满足要求，故而这种简化方式有其应用价值。2001年，Paperno等人也提出了采用两轴磁场源、三轴传感器的五自由度磁场跟踪方法。[13]

近年来，比较热门的磁场配置方式是采用传感器或磁场源阵列的方法。2001年，Schlageter等人[15]率先提出了基于2D霍尔传感器阵列的电磁跟踪方法，采用单个单轴圆柱形永磁体作为磁场源，4*4共16个3 cm间距的圆柱形霍尔器件作为传感器，利用无限远偶极子模型，采用迭代方法计算磁体三自由度的位置和两自由度的方向。由于磁体是轴对称的圆柱形，故第三个方向角即自传方向角无法测得，但五自由度对于很多应用已经足够。2003年，Plotkin等人[16]提出了一种对称的方法，采用8*8的线圈阵列作为磁场源，单个单轴线圈作为传感器，实现了一种采用AC磁场的基于线圈阵列的电磁跟踪方法。与Schlagerer等人提出的2D霍尔阵列的方法相比，信噪比最多提高三个数量级，对DC误差和1/f噪声不敏感，可同时跟踪多个对象。在算法方面，基本与Schlagerer的方法类似，但是在跟踪阶段减少了激励线圈的数目，以简化计算。由于这种阵列的方法只能实现5自由度，一些研究人员开始研究如何改进以实现六自由度的跟踪，例如，2009年Yang等人[17]提出采用使用方形永磁体代替圆柱形磁体的方法，给出了基于方形永磁体的磁场模型，并进行了一系列仿真验证了跟踪方法。

平面正三角形分布的三轴磁场源是另一种常见的方法。1995年Ben-Haim等人[10]提出，采用三个平面正三角形分布的磁场源，一个三轴磁场传感器进行磁场定位的方法。在手术床下布置三个三轴正交的励磁线圈为发射脉冲磁场，嵌有三轴磁传感器的单电极导管在心内移动，根据传感器的测得的场强实时计算其六自由度的位置和方向。该方法经过一系列专利的优化改进，1997年被成功运用于Bisense公司的CARTO三维心内膜标测系统中，成为第一套基于体外磁场的非X线心内导管实时定位和标测系统。2004年，Paperno等人[11]为解决两轴传感器的低分辨率区域问题，采用了三个平面三角形分布的三轴磁场源加一个两轴传感器的电磁跟踪方法，采用冗余设施较好的克服了低分辨率区域的影响。2002年， Govari等人[12]提出了一种只采用单轴传感器的方法。也通过采用非对称的传感器的方案，克服了单轴传感器只能实现五自由度的缺陷，实现了六自由度的定位。

此外，代表性的磁场配置方式还包括以下几种。1995年，Sasada等人[9]的提出的基于线性梯度磁场源的方法。采用交叉导线发生线性梯度磁场，使用磁通门传感器，三个正交方向采用不同的频率，测量传感器相对于初始位置的位移。2003年，Kirsch等人[14]提出一种方案，将六个磁场源置于正四面体的六条棱上，一个传感器置于正四面体外，可用单个/多个线圈、霍尔传感器或者其他，这取决于系统可实现5DOF还是6DOF。在磁场源和传感器几何形状方面，大多数方法均采用普通的圆柱形磁场源或传感器。但是单个轴对称的单轴传感器在实现六自由度的跟踪方面无能为力，因为它绕对称轴旋转之后接收到的磁场不会发生变化，为提高自由度，许多研究人员提出采用不对称的传感器[12,17]。采用无限远磁偶极子模型进行磁场近似与真实磁场会有一些出入，一些研究人员提出使用更精确的模型，但精确计算圆形导线的电流需要计算椭圆积分，计算量较大，因而Schneider等人[18]提出了使用方形导线绕制的线圈作为磁场源的方案。此外，Anderson等人还提出了一种采用PCB板制作的三角形天线，用于实现电磁跟踪。

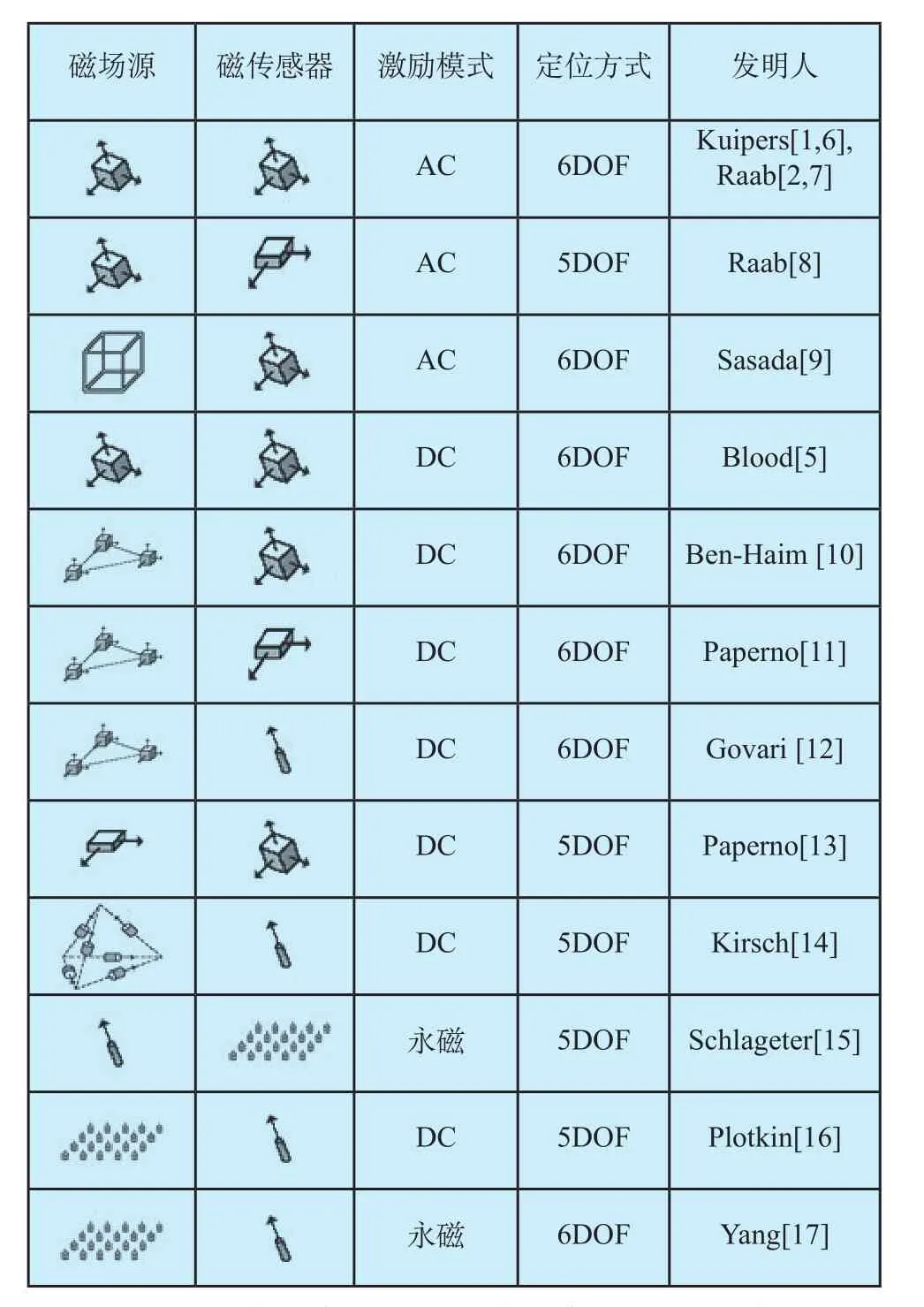
表1 电磁跟踪方法Table 1. Electromagnetic Tracking Methods

2 跟踪算法

电磁跟踪的过程一般分为两个阶段，初始阶段和跟踪阶段。初始阶段不知道待测单元的位置信息，可能需要在整个系统跟踪区域搜寻，故而耗时往往较长，过程较复杂。在实现初始定位之后，由于待测单元在短时间内不会有太大的移动，故可以知道待测单元的大致位置，这是往往可以以待测单元前一个时刻的位置作为初始位置进行搜寻，因为一般能够较快的实现定位，这一阶段称为跟踪阶段。

磁定位的跟踪算法主要有两大类，即迭代算法和非迭代算法。

2.1 迭代算法

迭代方法的基本思路[18]是基于某种磁场模型列出每个磁场源和传感器之间的磁场耦合方程，然后采用最优化算法（典型的如Levenberg-Marquardt最优化算法）迭代解出位置和方向的参数。耦合方程的数目必须超过未知数的个数，这样才可能得到收敛的结果，例如，六自由度的系统需要至少6个独立方程。在初始阶段，由于缺乏位置信息，一般假定一个或多个初始位置进行迭代，这种情况下往往耗时较长，且可能不能得到全局最优解。在跟踪阶段，由于初始位置靠近当前位置，故较易实现跟踪。为了使迭代能够达到全局最优解，研究人员提出了一系列改进方法，Kirsch提出[14]对迭代结果进行检验，另外一些人则尝试采用一些更好的全局最优化方法，如粒子群算法[17]等，或者采用线性算法做初始估计，然后使用迭代算法获得精确解[19]。

2.2 非迭代算法

由于迭代方法可能无法得到全局最优解，许多研究人员提出了一些非迭代的方法。Raab等人[7]提出了一种基于旋转变换的非迭代算法，该算法在已知近似位置和方向的情况下计算微小偏差以获得真实位置，由于利用了偏差微小的特点进行近似，所以在偏差较大的时候可能跟踪效果也会较差。Kuipers提出了[1,6]一种基于章动磁场的算法，调节三轴磁场使其合磁场指向待测目标，根据传感器波形判断位置，之后，他们又提出了一种再次基础上基于四元数旋转的改进快速算法[20]。

大多数算法需要依赖某种磁场模型，目前使用最为广泛的无限远偶极子模型[21]。该模型将磁场源抽象为一个磁偶极子，以计算其周围的磁场分布，模型计算简单，因而在大量电磁跟踪方法中得到广泛的应用。但是该模型仅当待测物体距磁场源距离远大于磁场源尺寸（如半径）的时候有效。为了克服这个缺陷，研究人员提出了一些改进方案。Jones等人[22]提出在使用无限远偶极子模型的同时在距离较近的时候进行一些补偿，他们利用拉格朗日级数实现。Kirsch等人[14]提出采用其他种类磁场，例如磁四极子磁场，以提高磁场分辨率。Schneider等人[18]提出了更为精确的基于线圈形状的磁场模型，他们给出了圆形导线和方形导线的磁场公式，并据此设计实现了电磁跟踪系统。Kranz等人[23]提出一种不采用磁场模型而直接标定磁场的自适应磁场跟踪方法，该方法能够很好的克服磁场模型与真实磁场分布不一致的缺陷，但是标定过程较为复杂。最近，本课题组提出了[24]一种采用磁棒搜索场强最大值的电磁跟踪方法，该方法不依赖于磁场模型，只利用几何算法实现定位，在算法方面有着独特的优势。

3 校准方法

校准对于一个电磁跟踪系统的性能有着举足轻重的影响。由于偶极子磁场的场强是随距离三次方下降的，在距离较远处，较易受到干扰，精度无法保证。特别是基于磁场模型的方法，由于磁场源的不规则等因素，按模型计算的磁场和真实磁场就会有较大的差距，校准显得尤为重要。

电磁跟踪的校准问题可以看作是三维空间的插值问题，测量一部分真实位置，寻找测量位置和真实位置的映射关系。Kindratenk等人对校准方法进行了总结[25]。校准方法大致可以分为两类：全局校准方法和局部校准方法，前者采用所有测量点作为所有位置的校准依据，后者测量点只影响周围位置的校准。

3.1 局部校准

Ghazisaedy等人[26]采用三线性差值方法，他们测量立方体顶点测量，在立方体内部采用线性算法差值。Zachmann等人[27]则提出采用模板函数的方法，这种方法不在要求测量空间为立方体，而可以是其他形状。这类局部校准方法有一个共同的缺陷，由于差值只在局部空间（如立方体）内进行，故只能保证每个空间内的连续性，而在空间的边界上则出现梯度跳变。

3.2 全局校准

Kindratenko等[28]提出基于高阶多项式匹配的校准方法，他们的方法能够在整个空间平滑，并可校准测量点之外的空间。研究发现，三阶或四阶多项式比较适于标定，过高阶数则可能导致震荡。这种方法在校准较大误差的时候有良好效果，但在误差很小的情况下可能引入额外误差。Saleh等[25]提出采用神经网络的方法，他们尝试了多层前馈神经网络，认为带有两个隐含层的神经网络可以较好的满足要求，也可以实现整个空间的平滑。但并未证明采用的神经网络结构是否最优，而且神经网络的方法在训练过程中耗时很长。

4 总结

至此，本文对电磁跟踪发展过程中的主要方法和算法进行了简单的归纳和总结。从Kuipers和Raab等提出基本的电磁跟踪方法开始，经历了三十多年的发展。在磁场配置方式、激励方式、器件的几何结构以及跟踪和标定算法等各个方面有许多尝试和改进。减少干扰和提高精度是电磁跟踪发展的两大主题，所有的尝试和改进都是围绕着这两大主题进行的。虽然目前电磁跟踪技术已经有了长足的进步，出现了一些专业的公司和临床试用的产品，但这一技术离实际大规模的使用还有着很大的距离，研究工作仍然还需要继续。这一技术有着很多自身独特的优势，相信经过进一步的研究改进，一定能够得到越来越广泛的应用。

[1] Kuipers J. Object tracking and orientation determination means,system and process[P]: US, 3868565. 1975-2-25

[2] Raab F H. Remote object position locater[P]: US, 4054881. 1977-10-18

[3] Schneider M R. Electromagnetic tracking for catheter localization[A]. Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series[C], 1999, 61-68.

[4] Scully J T, Schneider M R. DC magnetic-based position and orientation monitoring system for tracking medical instruments[P]: 20070078334. 2005-10-4

[5] Blood E B. Device for quantitatively measuring the relative position and orientation of two bodies in the presence of metals utilizing direct current magnetic fields[P]: US, 4849692. 1990-7-31

[6] Kuipers J. Method and apparatus for tracking objects[P]: 4298874.1978-10-24

[7] Raab F H, Blood E B, Steiner T O, et al. Magnetic position and orientation tracking system[J]. IEEE Transactions on Aerospace and Electronic Systems, 1979, 15(5): 709-718.

[8] Raab F H. Remote object position and orientation locater[P]:4314251. 1979-7-30

[9] Sasada I, Yamauchi T. Vibrational noise canceling technique for low-frequency, low-level magnetic field measurement[J]. IEEE Transactions on Magnetics, 1995, 31(6): 3406-3408.

[10] Ben-Haim, Il S H. Apparatus and method for ablation[P]:5443489. 1994-9-23

[11] Paperno E, Keisar P. Three-dimensional magnetic tacking of biaxial sensors[J]. IEEE Transactions On Magnetics, 2004, 40(3):1530-1536.

[12] Govari A. Electromagnetic position single axis system[P]: US,6484118. 2002-11-19

[13] Paperno E, Sasada I, Leonovich E. A new method for magnetic position and orientation tracking[J]. IEEE Transactions on Magnetics, 2001, 37(4): 1938-1940.

[14] Kirsch, de Ch S R L S. Errors in systems using magnetic fields to locate objects[P]: 6553326. 2000-7-4

[15] Schlageter V, Besse P A, Popovic R S, et al. Tracking system with five degrees of freedom using a 2d-array of hall sensors and a permanent magnet[J]. Sensors and Actuators A-Physical, 2001,92(1-3): 37-42.

[16] Plotkin A, Paperno E. 3-d magnetic tracking of a single subminiature coil with a large 2-d array of uniaxial transmitters[J]. IEEE Transactions on Magnetics, 2003, 39(5):3295-3297.

[17] Yang W A, Hu C, Meng M, et al. A six-dimensional magnetic localization algorithm for a rectangular magnet objective based on a particle swarm optimizer[J]. IEEE TRANSACTIONS ON MAGNETICS, 2009, 45(8): 3092-3099.

[18] Schneider M. Measuring position and orientation using magnetic fields[P]: US, 6073043. 2000-06-06.

[19] Hu C, Yang W, Chen D, et al. An improved magnetic localization and orientation algorithm for wireless capsule endoscope[C].30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2008, 2055-2058.

[20] Kuipers J. Method and apparatus for determining remote object orientation and position[P]: 4742356. 1985-12-9.

[21] Hansen P K. Magnetic position and orientation measurement system[P]: US,4622644. 1986-11-11

[22] Jones H R. Method and apparatus for determining remote object orientation and position[P]: 4737794. 1985-12-9

[23] Kranz Y, Kornblau G, Stokar S. Adaptive magnetic tracker: a revolution in electromagnetic tracker technology[C]. Helmetand Head-Mounted Displays IX: Technologies and Applications,2004, 149-156.

[24] Ge X, Lai D, Wu X, et al. A novel non-model-based 6-DOF electromagnetic tracking method using non-iterative algorithm[C].The 31st Annual Conference of IEEE EMBS, Minneapolis, MN,US, 2009,

[25] Kindratenko V. A survey of electromagnetic position tracker calibration techniques[J]. Virtual Reality, 2000, 5(3): 169-182.

[26] Ghazisaedy M, Adamczyk D, Sandin D J, et al. Ultrasonic calibration of a magnetic tracker in a virtual reality space[C].1995, 179-188.

[27] Zachmann G. Virtual reality in assembly simulation - collision detection, simulation algorithms, and interaction techiques[D].2000.

[28] Kindratenko V. Calibration of electromagnetic tracking devices[J]. Virtual Reality, 1999, 4(2): 139-150.