基于金字塔连接与高斯混合模型算法的层析芯片荧光信号检测

【作 者】胡贝贝，张雪青，陈昊鹏，崔大祥

1 上海交通大学，软件学院，上海市闵行区东川路800号，200240

2 上海交通大学微纳科技研究院

免疫层析芯片是一个很好的快速检测病原体的方法，它是以抗原或抗体作为检测对象，利用抗体与抗原的特异性结合的免疫反应，实现对待测物的定量分析[1]。

采用新型的纳米粒子，如磁性荧光纳米粒子或量子点作为层析芯片的标记物是一种新的方案，可以显著提高检测的灵敏度[2]。芯片上荧光区域的亮度就反映了抗原抗体之间的相互作用的情况，可以通过提取荧光信号来达到疾病检测的目的。实验通过对一组由不同浓度的抗原——抗体的免疫反应产生的荧光区域的亮度的计算，来定量地分析抗原浓度与荧光亮度之间的对应关系，从而达到病毒检测的目的。

为了更好地提取免疫层析芯片荧光信号的信息，根据层析芯片图像的特点，本文提出了一种新的算法，来检测出荧光区域信号。此算法首先用基于RGB空间的数学形态学运算对图像滤波增强[3]，并采用金字塔连接算法分割图像[4、5]，然后使用高斯混合模型（GMM）[6]检测荧光信号，以准确地提取出荧光区域的轮廓，最后再计算荧光区域的平均亮度并对其作定量分析[7]。通过多次实验验证，该方法对荧光信号的检测具有很好的效果。

本文先介绍算法的相关背景知识，提出新算法，包括数学形态学滤波、金字塔连接和高斯混合模型；然后通过实验数据分析进一步验证算法的有效性；最后再对这种荧光信号的检测算法进行归纳总结。

1 背景知识

1.1 彩色数学形态学

免疫层析芯片在制备、清洗、扫描的过程中必然会产生随机的噪声，这些噪声在图像中会对荧光信号的识别造成影响。采用彩色图像形态学的方法进行滤波处理，基于RGB彩色空间，采用平面结构元素的彩色形态变换方法[8]。

V(x)为RGB空间的彩色图像，P为平面结构元素，且P∈Z2，数学形态学运算可表示如下：

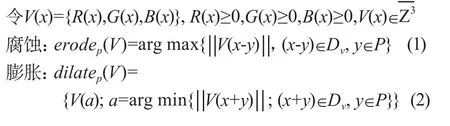
结构元素P的选取与采集芯片图像的荧光区域大小和噪点大小有关[9]，在对免疫层析芯片图像滤波增强时，既要保留荧光区域，又要去除掉背景噪声。

1.2 金字塔分割

金字塔由一系列级组成，越高级别信息量越少，每一步向更高级别变换用信息缩减的分析算子实现，而每一步向更低级别变换用信息保留的合成算子实现[10]。通常金字塔的低分辨率图像用于分析大的结构，而高分辨率图像用于分析单个部分的特性。

金字塔分割的一般过程是首先要建立金字塔的简单系统，在建立完金字塔后，相邻层之间就形成了父子关系。设置两个阈值threshold1和threshold2，threshold1是建立连接的错误阈值，threshold2是分割簇的错误阈值。如果层i与其邻层的灰度值差小于threshold1，则在层i的像素点a与其邻层的父亲像素点b之间建立连接，在定义好连接部件后，它们被加入到某些簇中；如果a与b之间的平均灰度值差小于threshold2，则两个像素点属于同一簇。

1.3 高斯混合模型（GMM）

高斯混合模型（Gaussian Mixture Model, GMM)[11]是单一高斯概率密度函数的延伸，能够平滑地近似任意的密度分布。混合高斯模型的概率密度函数是由M个高斯概率密度函数的加权求和得到：

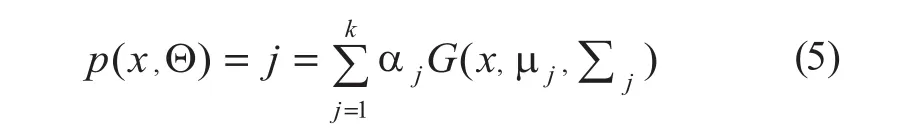
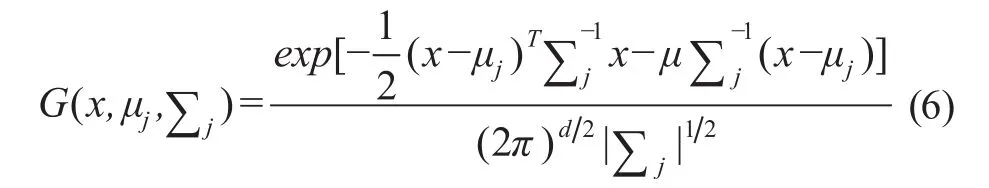
其中，μj是均值向量，∑i是协方差矩阵。图1是一个k =3的高斯混合模型。

完整的高斯混合模型由参数均值向量、协方差矩阵和混合权重组成，表示为：

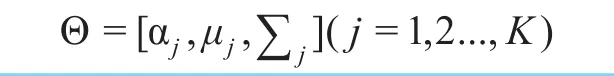
2 荧光信号的检测算法

首先对免疫层析芯片图像进行滤波增强，由于形态学噪声操作只能消除那些比结构元素小的噪声，所以结构元素选用的全黑模板。在形态学的图像应用中，开运算常用来实现滤波，闭运算通常用来滤除较小的暗细节。开和闭不互为逆运算，本文采用级连使用应用于层析芯片图像。结合荧光信号的特点，采用开闭级连的方法，可以有效抑制图像的噪声，为后面的图像分割做好准备。

在对芯片图像进行形态学滤波后，采用金字塔连接算法[12]对图像进行初始分割，分割出背景并保留荧光区域的特征。在金字塔的最底层，节点数为原始图像的象素个数。每一个节点都包含了根据计算图像而得到的特征值。当向金字塔的上层移动时，尺寸和分辨率就降低，而高层图像中的节点的初始值由低层节点的均值计算而来。在整个金字塔建立起来后，从金字塔的底部开始，相邻层的各个节点建立连接。相邻层各节点的关系称为父子关系。这种算法的迭代过程如下：

(1) 计算高斯金字塔。实验中选用GAUSSIAN_4x4模板来建立金字塔。

(2) 建立父子关系。在计算出高斯金字塔后，相邻层之间就形成了父子关系。第l层金字塔中的节点(i,j)所包含的特征值有4个：① 局部图像特征值c[i, j, l][t]；② 特征的面积a[i, j, l][t]；③ 指向父结点的指针p[i, j, l][t]；④分割特征，即整个分割区域包含节点的平均值s[i, j, l][t]。字母t表示迭代次数(t ≥ 0)。对于第l层的每一个节点(i,j)，在第l-1层有16个可选取的子节点(i', j')，在l+1层有4个可选取的父结点(i'', j'')。在金字塔顶层以下的各层中，对于每次迭代t，所有节点都建立了父子关系。

(3) 将连接的像素平均。定义了父子关系之后，t,c和a的值从最底层向最高层(0≤l≤n)计算，a[i, j, 0][t]=1，c[i, j, 0][t]=c[i, j, 0][0]，a[i, j, l][t]=∑a[i', j', l-1][t]其中求和是计算节点(i, j)所有子节点的和。如果a[i, j, 0][t]=0，则没有子节点；如果a[i, j, l][t]＞0则c[i, j, l][t]=∑(a[i', j',l-1][t]c[i', j', l-1][t])/a[i, j, l][t]，通过c的变化来控制迭代过程。在每一层l，每个节点的s值就是它的父结点的c值，即s[i, j, l][t]=c[i", j", l+1][t]。当t次迭代完成后，第t+1次迭代就开始；当c没有变化时，迭代过程就结束。

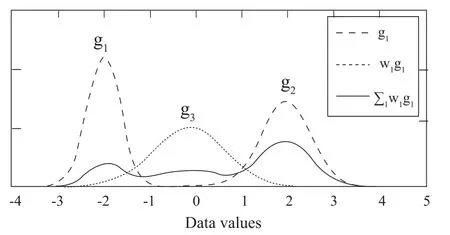
图 1 高斯混合模型(K=3)Fig.1 Gaussian Mixture Model(k=3)

在金字塔算法对芯片图像初始分割后，采用高斯混合模型对荧光信号进一步检测，算法主要步骤如下：

(1) 根据金字塔分割出的背景区域与前景区域，我们选出感兴趣的荧光区域部分；

(2) 结合这些荧光区域的颜色信息，通过EM算法估计出了GMM的各个参数值，把图像的背景与前景分别用GMM近似估计概率分布。EM算法包括两个步骤：由E步和M步组成，它是通过迭代最大化完整数据的对数似然函数的期望来最大化不完整数据的对数似然函数。E-步，计算完整数据的对数似然函数的期望；M-步，通过最大化期望来获得新的参数Θ。通过交替使用这两个步骤，EM算法逐步改进模型的参数，使参数和训练样本的似然概率逐渐增大，最后终止于一个极大点，最后则实现参数的估计，生成一个高斯分布。

(3) 把图像的背景与前景分别用GMM去近似估计概率分布。通过实验知道，当参数K为6时，可以得到较好的效果。遍历图像的每个像素，分别计算每个像素属于背景与前景的概率，比较这两个概率，将该像素化到概率大的一方中。遍历完整个图像后，则得到分割后的荧光区域。

3 实验结果分析

3.1 图像滤波增强处理结果

为了简洁地说明问题，检验上述所提算法的有效性，我们选取一幅免疫层析芯片图像进行分析，原图像如图2a所示。

图2 图像滤波后的结果Fig.2 The results after image filtering

根据采集的免疫层析芯片图像的特点，为了更好的去除噪声增强荧光信号，选取了9x9的全黑模板，并采用了开闭级连，对RGB空间的图像进行了彩色形态学变换。图像滤波后的结果如图2b所示。

对于试纸条的层析芯片图像，我们最终需要提取的是图像中上下两部分黄色荧光条带部分（即检测带和质控带）。从原始图2a中可以看出背景中存在了很多的噪声，通过图2b可以看到，荧光区域之外的背景噪声有了一定程度的去除，荧光信号就更加明显，从而为后面的图像分割做好准备。

3.2 荧光信号轮廓提取

图2b是采用金字塔算法对生物芯片图像进行初步分割的结果。从原始图像和金字塔分割后的图像灰度直方图(图3d、3e)对比也可以看出，金字塔连接算法有效地对芯片图像进行了预处理，去除了很多背景干扰噪声，增强了图像的对比度，在此基础上再用GMM分割荧光区域从而获得最终的黄色荧光区域的轮廓，实验效果图如图3c所示：

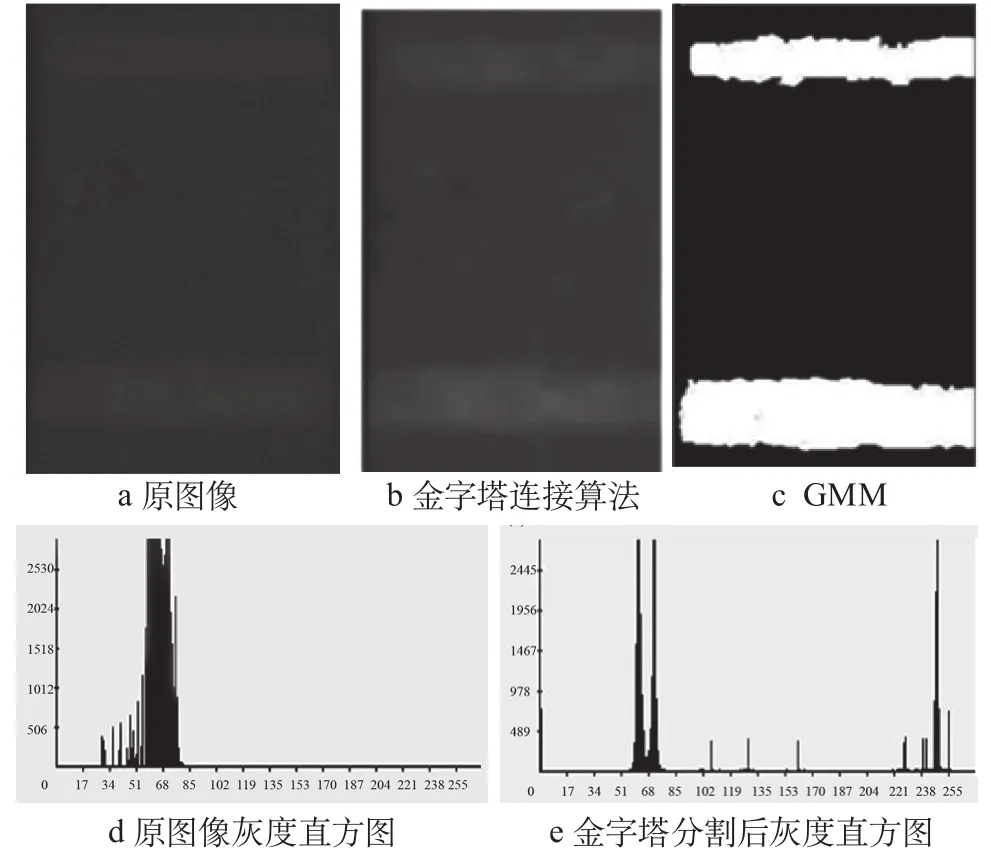
图3 荧光区域提取结果Fig.3 Fluorescent segmentation results

3.3 荧光信号的数据分析

平均法，是一种广泛使用的统计方法，通过统计出的荧光信号区域内所有像素点光密度的平均值来反映荧光区域的荧光强度。抗体与不同浓度的抗原相结合，荧光的亮度就反映了抗原抗体之间相互作用的情况。通过前面提到的算法实现自动提取出荧光区域，再计算出提取的荧光区域的平均亮度，就可以定量地分析参与反应的抗原的浓度与荧光亮度间的对应关系。

针对采集的一组不同浓度抗原与抗体结合的免疫层析芯片图像，由本文算法自动提取荧光区域的轮廓并计算荧光亮度，根据检测的数据得到图4和表1。

图4表示抗原浓度与荧光亮度之间的对应关系，由表1的数据拟合而成的直线，f(x)=883.53487x+133.58974,拟合度达到0.9926。可以看出，检测出的荧光区域的平均亮度与参与反应的抗原浓度呈一定的线性关系，从而为层析芯片信息的定量分析提供了依据，也验证了算法的有效性和精确性。

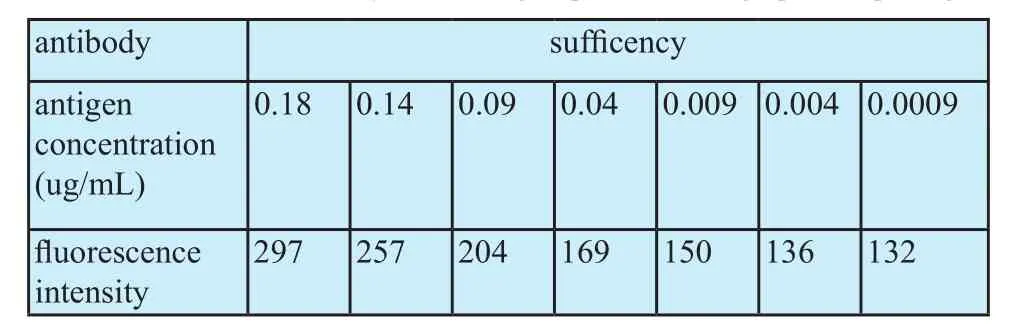
表1 量子点标记的不同浓度的抗原与抗体充分结合后产生荧光的亮度值Tab.1 Fluorescence intensity value of a group of chromatographic chip images

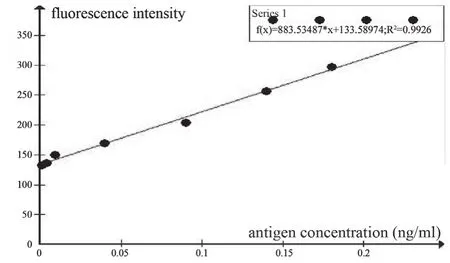
图4 抗原浓度与荧光亮度之间的对应关系Fig. 4 Linear relation between fluorescence intensity and concentration of antigens

4 结论

由实验结果可以说明，本文采用的算法对于层析芯片的荧光信号的检测具有很好的效果，能够准确地检测出荧光信号，从而实现免疫层析芯片的定量分析。利用了金字塔的分割特性，计算快速简单且执行效率高，而采用高斯混合模型，可以有效地进一步分割图像，并精确地提取出荧光区域的轮廓。该方法可以有效地针对量子点标记的免疫层析芯片进行荧光信息的自动提取。

[1] H.Arai, B. Petchclai, K. Khupulsup, T. Kurimura, K. Takeda.Evaluation of a rapid immunochromatographic test for detection of antibodies to human immunodeficiency virus[J]. J Clin Microbiol,1999, 37:360-70.

[2] H. Yang, Q. Guo, R. He, et al. A Quick and Parallel Analytical Method Based on Quantum Dots Labeling for ToTCH-Related Antibodies[J]. Nanoscale Research Letters ,2009,4: 1469-1474.

[3] L. A. Overturf, M. L. Comer, and E. J. Delp. Color image coding using morphological pyramid Decomposition[J].IEEE Trans.Image Process, 1995, 4: 177-185.

[4] M. Bister, J. Cornelis and A. Rosenfeld. A critical view of pyramid segmentation algorithms[J]. Pattern Recog. Lett,. 1990,11: 605–617.

[5] D. Prewer and L. Kitchen. Soft image segmentation by weighted linked pyramid[J]. Pattern Recog. Lett, 2001, 2:123–132.

[6] Z. Zivkovic. Improved adaptive gausian mixture model for background subtraction[J]. Proc. Int. Conf. Pattern Recognition,2004, 2: 28–31.

[7] Xujing Wang*, Soumitra Ghosh and Sun-Wei Guo. Quantitative quality control in microarray im-age processing and data acquisition[J]. Nucleic Acids Research, 2001, 15:75.

[8] Robert HIRATA Jr., Junior BARRERA. Microarray gridding by mathematical morphology[A]. Pro-ceedings of XIV Brazilian Symposium on Computer Graphics and Image Processing[C].IEEE 2001: 112-119.

[9] J. Electron. Morphological operations for color image processing[J]. Electrical Imaging, 1999, 8:100-103.

[10] Goutsias J. Non Linear Multiresolution Signal Decomposition Schemes-Part I: Morphological Pyramids[J].IEEE Trans on Image Processing, 2000, 9(11): 1862-1876.

[11] Carsten Rother, Andrew BLAKE,et al. Grabcut - interactive foreground extraction using iterated graph cuts[J]. In Proceedings of ACM SIGGRAPH, 2004, 3: 309-314.

[12] Jahne B. Digital Image Processing[M]. New York: Springer, 1997.