弥散斑验光仪的设计
2011-01-26张逸夔黄胜海叶慧芳邹睿韬童耿民卓然陶育华
【作 者】张逸夔,黄胜海,叶慧芳,邹睿韬,童耿民,卓然,陶育华
温州医学院眼视光学院,浙江省,温州市,325027
0 引言
弥散斑在日常生活中很常见,在夜晚中看远处的路灯,人们会发现,戴和不戴眼镜所看到的路灯形态不同,这是因为屈光状态的不同而造成眼底弥散斑形态、大小的改变。利用这个原理,弥散斑验光仪能让医生半定量地了解到患者眼中的弥散斑,并利用计算机分析患者的屈光状态,从而有助于临床诊断和开具处方。
1 弥散斑验光仪的原理和结构
1.1 弥散斑的计算原理
1.1.1 用emsley标准简化眼来进行理论分析
根据简单的三角形相似和公式L'-L=Fe(L' 为像方屈光度,L为物方屈光度,Fe为眼屈光度),可得

如图1所示,j为视网膜上弥散斑大小,g为瞳孔大小,K为近(远)点屈光度,K'=Fe+K。由Zemax模型眼计算得NO' =16.58 mm,fe=16.56 mm,因此Fe=1000/fe≈1000/NO',其中NO'为节点到视网膜的距离,fe为眼球前焦距。
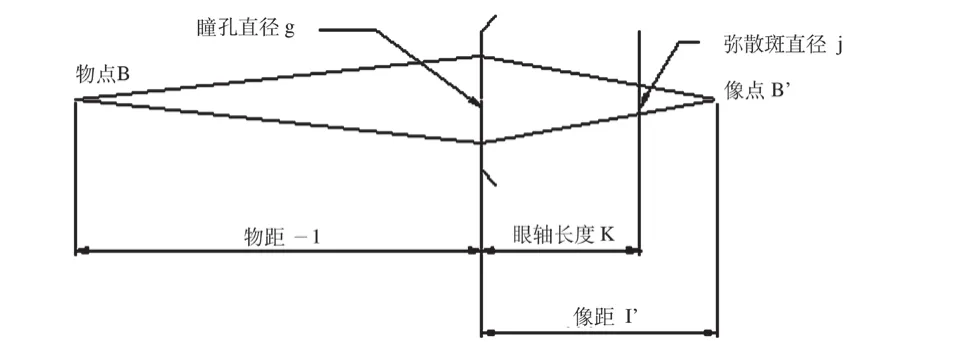
图 1 简化眼模型示意图[1]Fig.1 The diagram of reduced eye model
把该视网膜上的弥散圆直径换算到5米远处相应的光斑直径ja,如图2所示,即有

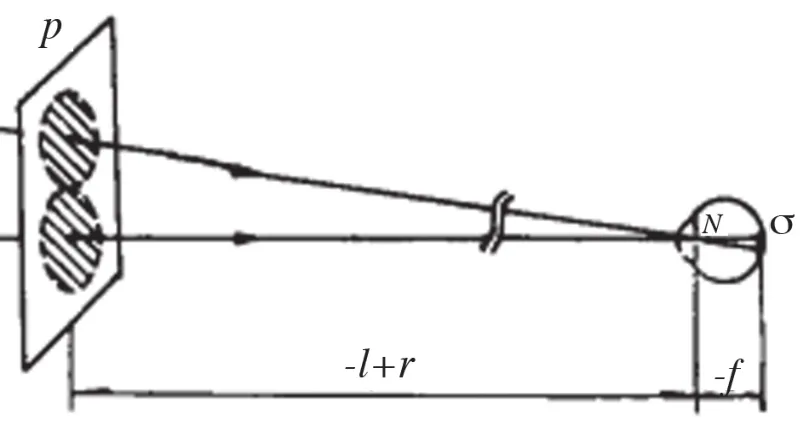
图 2 简化眼光路示意图[2]Fig.2 The optical path of reduced eye model
式中,-l为物距,r为角膜曲率半径,NO' 为结点到视网膜的距离。
当物是一定大小的物体时,则应将ja值再加上该物体的高度h, 即

这里jh即为患者所见屏上光斑的大小[2],我们通过测量jh,可获得患者的K,即屈光度数。
1.1.2 Zemax光学设计软件仿真
由于上述(1)~(3)式由简化模型眼推导而来,未必符合复杂的人眼。因此,利用Liou & Brennan 1997 eye model进行Zemax计算机仿真,以验证公式的合理性。
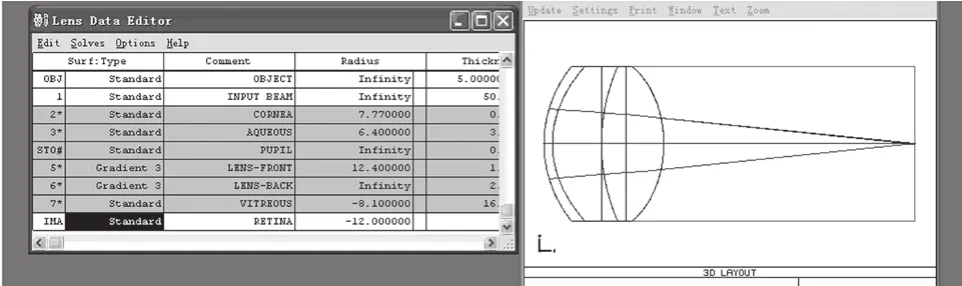
图 3 Zemax 人眼模型Fig.3 Human eye model in Zemax
在此,我们主要关注视网膜弥散斑的大小是否符合公式(1)的推导结果。由于患者所见为周边有毛刺干扰的弥散斑,而在实际测量中我们让患者忽略毛刺的影响;因此在Zemax中我们选择RMS RADIUS,而非GEO RADIUS来代表人眼视网膜上的弥散斑大小。利用轴性近视的原理,通过改变视网膜的前后位置来模拟不同的屈光度。如图4所示,低度近、远视患者的眼底弥散斑很不规则;而随着屈光不正程度的上升,弥散斑能量分布越来越均匀。这和我们临床试用时的结果一致,即低度近视患者看到的毛刺很长、很明显,而高度近视患者的毛刺不太明显。
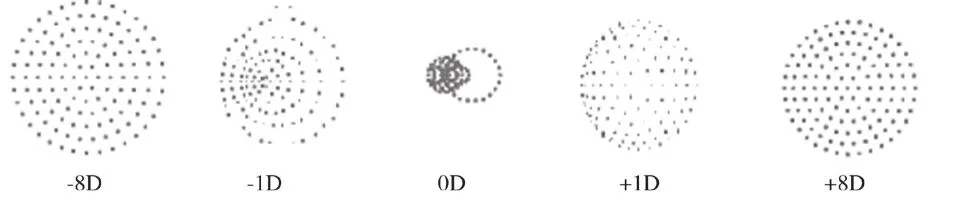
图 4 Zemax软件中不同屈光度下弥散斑的形态Fig.4 light intensity distribution of blur circle with different diopters
将公式(1)和Zemax中RMS进行比较(如图5),结果比较接近;而在高屈光不正区,两者差别相对比较大,这和RMS(均方差)的原理有关。当数据分布均匀,如呈正弦函数分布,则RMS=A/1.414(A为振幅),比实际的振幅A小。由于高度近、远视所看到的弥散斑更均匀,因此RMS比实际尺寸小。

图 5 简化眼和Zemax模型眼的视网膜弥散斑直径比较Fig.5 The comparison of blur circle’s diameter between reduced eye model and the Liou & Brennan 1997 eye model in different diopters
由此可知,公式(1)虽然是由简化眼模型推导而来,但具有较高的准确性。下文中的临床测试结果也证实了这一点。
1.2 弥散斑验光仪的结构
如图6所示,HE-NE激光发出波长632.8 nm光束,经过半反半透镜分为两束,透射的光束经过两面偏振片打到散射屏上,反射的光束经过平面反光镜达到散射屏上,形成两个光点。偏振片的作用是调节投射光的光强,使屏幕上的两个光点亮度相同。
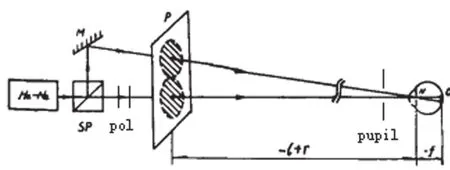
图6 弥散斑验光仪结构图[2]Fig.6 Structure diagram of blur circle refractometer
被测者距离散射屏5 m远,前置直径4 mm光阑,看到的光点为弥散斑。由上述理论推导可知,近、远视患者看到圆形弥散斑,散光患者看到椭圆。通过控制反射镜的上下左右摆动,被测者可以二维移动反射的光点,直至其认为两个弥散斑相切。此时测量两个光点的距离,两点连线和水平线的夹角,就可以通过公式来计算患者的屈光度数。如图7,对于散光患者,两个椭圆弥散斑短轴相切的结果为球镜度数,长轴、短轴相切结果之差为散光度数,长轴的夹角经过互补、转90o两步换算即为散光轴向。(说明:患者所见和验光师所见为镜面对称,验光处方中的轴向以验光师的角度为准,因此需要互补;对于柱镜来说,轴向和有屈光力的方向成90o,因此需要转90o)

图 7 散光患者所见的椭圆弥散斑长、短轴相切Fig.7 The elliptical blur circles should be moved to be tangent in the directionsof both major axis and minor axis when the patient is astigmatic
1.3 弥散斑验光仪的参数设计
由于个体差异,每个人的瞳孔大小,节点位置等参数与模型眼有所不同,为了验光的准确,我们需要设计这些参数,减少个体差异带来的验光误差。
1.3.1 瞳孔直径的设计
瞳孔大小是影响弥散斑的重要因素,我们将其设为4 mm。其理由如下:当瞳孔太大,球差增大,即患者所见毛刺增多,影响判断;当瞳孔太小,屏上点距离jh的测量误差造成的验光误差增大,节点位置的不同(个体差异)造成的系统误差也增大。
像差分析:对于无散光患者,由Zemax--Prescription分析得(表1所示),像差主要为球差和位置色差(无散光患者)。由于采用He-Ne激光,消除色差。对于散光患者,本质是不同子午线的屈光程度不同,像散的结果已经在测量长、短轴之差中反映,从而不再赘述。

表1 无散光患者的像差分析Tab.1 The aberration analysis of patients without Astigmatism
图8为Zemax中视网膜面Fan像差分析,x轴为相对瞳孔直径,Px 和Py分别为水平和垂直方向的瞳孔直径。由图可知,瞳孔增大,像差(球差)显著增大。由于球差大,患者所见的弥散斑毛刺增多,影响判断,从而不宜选用大瞳孔。
图9为不同屈光度下,瞳孔改变0.1 mm对验光结果的影响。由图9可知,验光结果对瞳孔的变化比较敏感,并且近视度数越大,对瞳孔变化越敏感。如近视-8D,瞳孔改变0.1 mm,造成0.25D的验光误差,因此患者需要前置光阑来控制瞳孔直径。
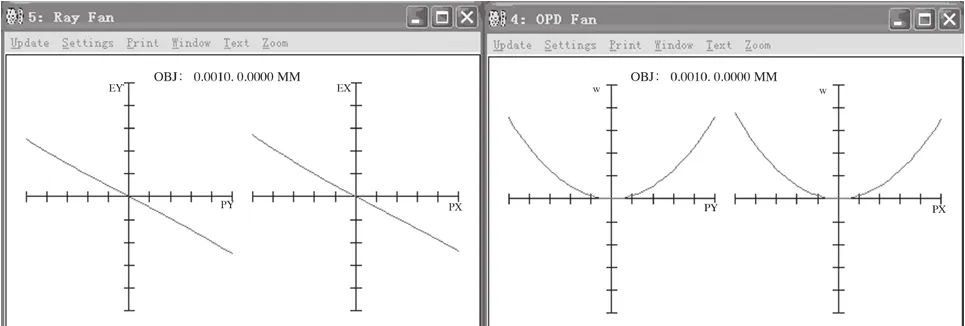
图8 Zemax-fan 像面垂轴像差分析Fig.8 The Ray Fan and OPD Fan analysis in zemax
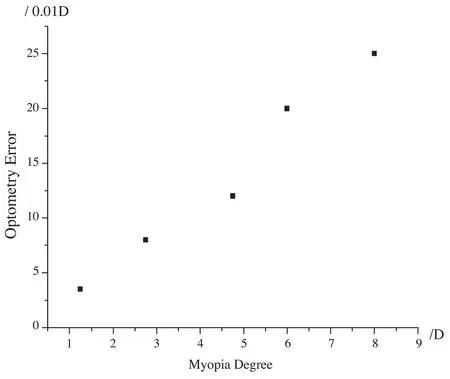
图9 近视程度越深,0.1 mm的瞳孔直径变化对验光结果的影响Fig.9 0.1 mm change of pupil diameter has greater impact on the optometry result in high myopia than that in low myopia
图10为屏上两光斑距离jh的测量误差敏感性分析。可知瞳孔直径越大,测量误差引起的验光结果改变越小。如瞳孔直径取2.5 mm,则1 mm测量误差造成0.1 D的验光误差。而若瞳孔直径取5.0 mm,则1 mm测量误差只导致0.05 D的测量误差。这体现了大孔径的优势。
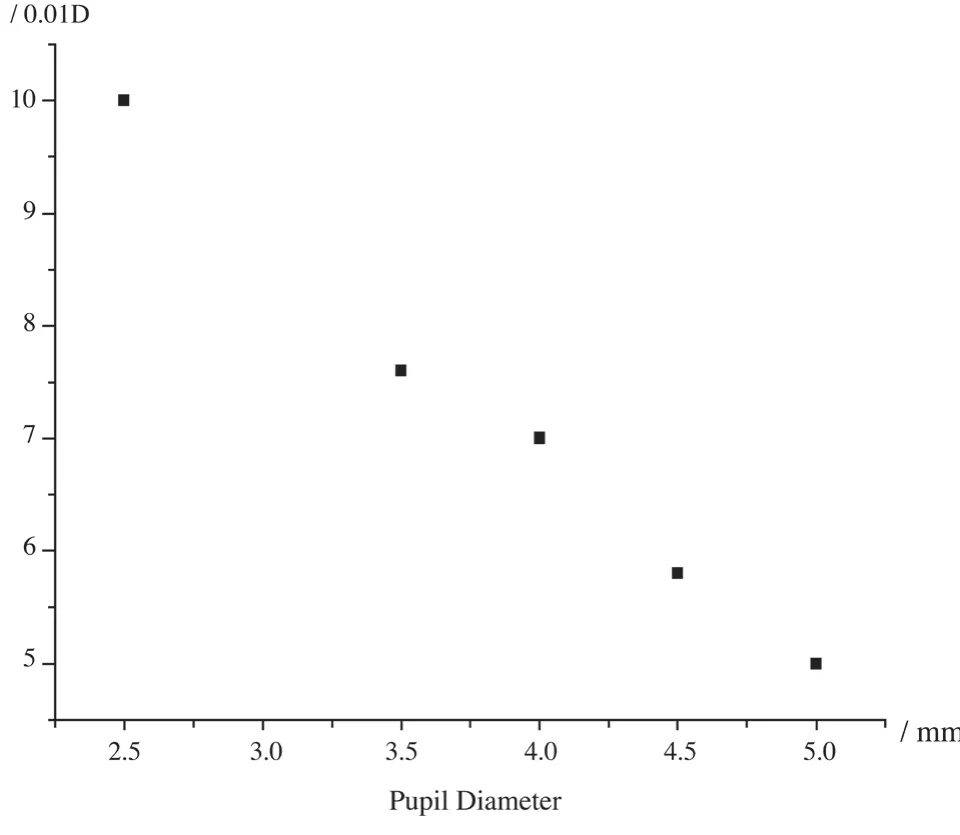
图10 瞳孔直径越大,1mm测量误差造成的验光误差越小Fig.10 1mm measurement error has greater impact on the optometry result in small pupils than that in large pupils
图11和12为孔径取4 mm时的误差敏感性分析。由图可知,当瞳孔取4 mm,节点位置的改变或测量误差对验光结果影响相对小,且屈光不正度数越低,验光误差越小。如近视-8D,测量误差或节点改变3 mm,验光结果变化小于0.25D,而近视-3D的结果变化为0.03D。
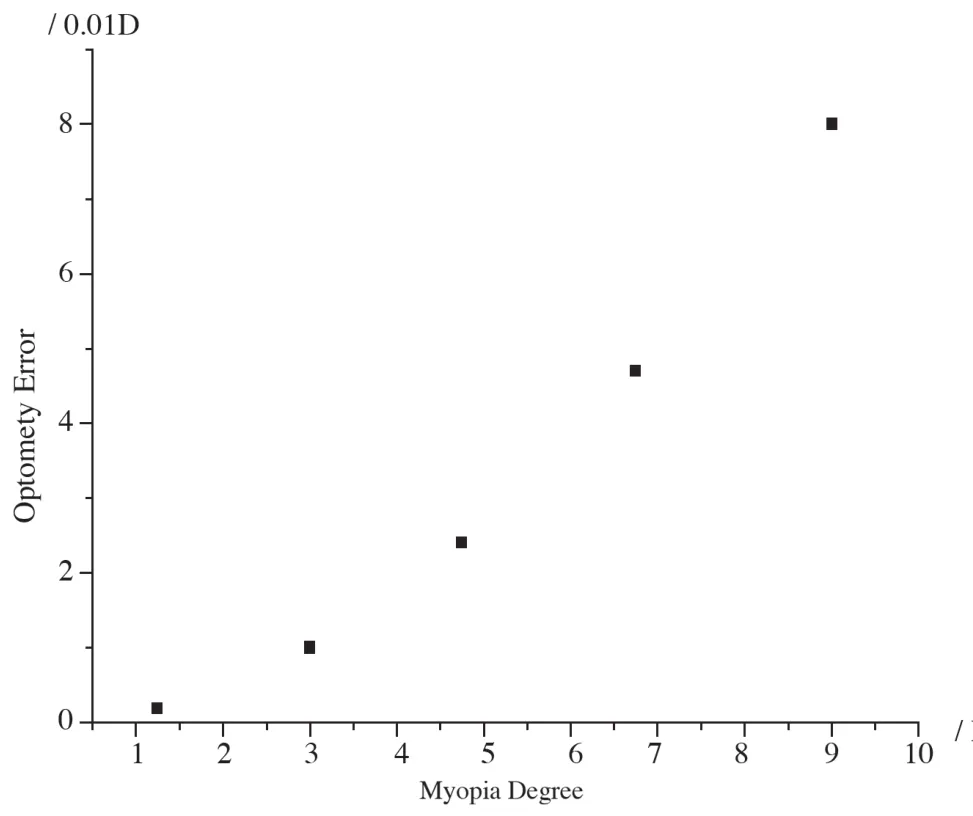
图11 瞳孔取4 mm时,1 mm节点位置变化对不同屈光度的验光结果的影响Fig.11 optometry error dot to 1mm NO' shift
综上所述,瞳孔取4 mm,不仅有利于改善弥散斑像质,而且能允许较大的个体参数差异和测量误差。
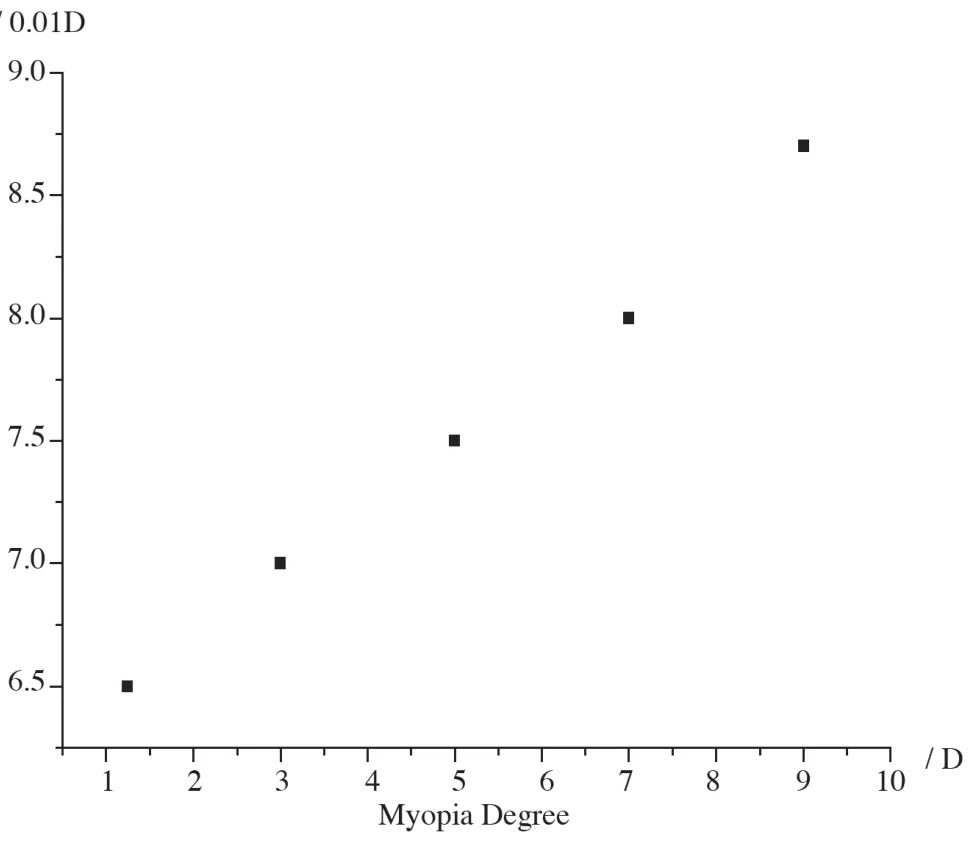
图12 瞳孔取4 mm时1 mm测量误差对验光结果的影响Fig.12 Optometry error dot to 1 mm jh measurement error
1.3.2 NO'长度的选择
Gullstand模型眼中眼轴长度为23.89 mm,节点大致位于晶状体后表面,NO'为16.53 mm。但不同个体眼轴长度不同,节点位置也不同。国内大多数数据表明[3-5],成人眼轴长度在22~28 mm之间,按比例计算,NO'大致在15.2~19.4 mm之间。在计算中,统一取NO'=20 mm,接近高度近视患者的NO',因为由图11可知,近视程度越高,节点位置变化越敏感。当患者为近视-9D,节点变化3 mm。引起0.25 D的验光误差;而当患者为近视-3D,节点变化3 mm。引起0.03 D的验光误差。因此NO'=20 mm可以有效地减少个体节点位置不同引起的测量误差。
2 仪器初步临床应用和评价
2.1 对象
近视数据21眼(42例),为在校学生和教师,矫正视力大于0.8;散光数据35眼(59例),轴向数据26例,均为温州眼视光医院视光部就诊患者,矫正视力大于0.6,散光度数大于0.75 D,年龄12~38岁,有认知能力,能判断椭圆相切。
2.2 方法
在室内光照度小于20 lx下,利用自行搭建的仪器进行测量,并将结果和医院的综合验光处方进行比较。
2.3 统计学方法
采用spss13.0 ,wps office 2005统计软件。将近视、散光度数、轴向数据和医院验光处方进行对照t检验,令P<0.05为具有统计学差异;将散光度数和医院验光处方差值按<0.25D、<0.5D、<0.75D、>0.75D共4组进行百分比分析。
2.4 结果
近视组和轴向组t检验结果阴性(P=0.33;P=0.086),无统计学差异;散光组对照t检验有统计学差异(P=0.041)。散光度数组比率如图12所示,<0.75D组为80%。散光组数据和医院结果偏离较大,可能和年幼患者配合有关。表2为对照t检验结果。
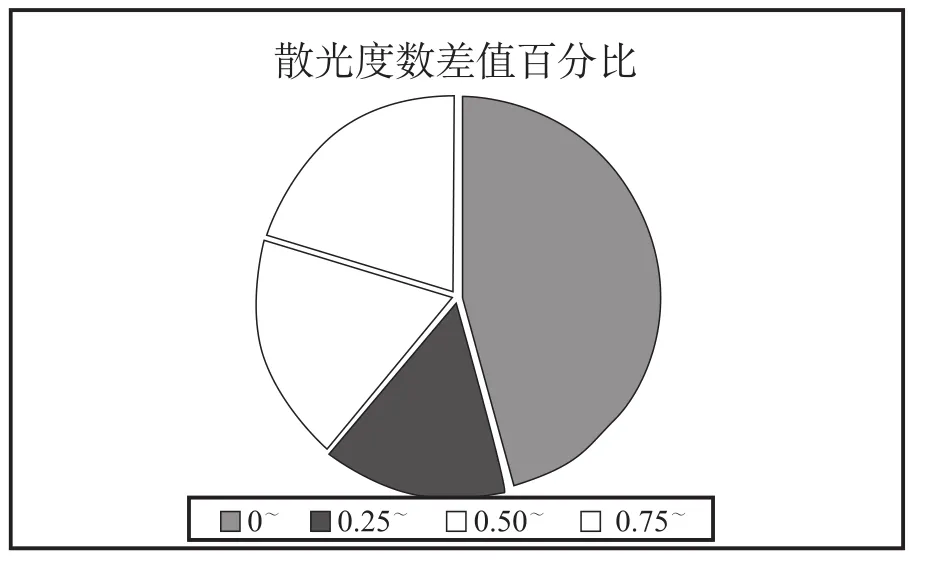
图12 散光测量结果Fig.12 Measurement results of astigmatism
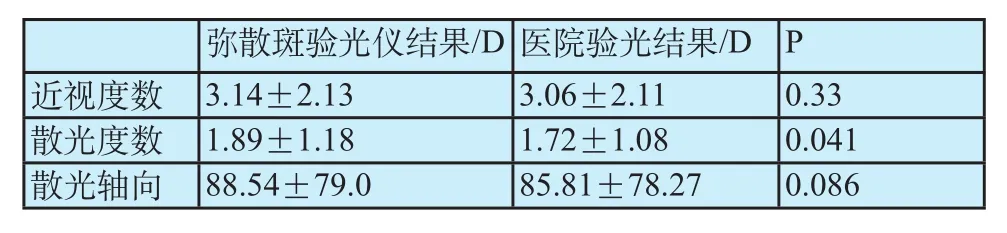
表2 对照t检验分析Tab.2 The results of paired t-test
3 讨论
早在几十年前,人们已经认识到屈光不正会导致眼底弥散斑的形态改变,并由简化眼推导出计算公式[1]。在90年代,我国学者也曾提出利用弥散斑进行验光的设想[2]。但由于简化模型眼精度有限,而复杂的眼模型又需要测量大量的个体参数,因此不利于临床应用。笔者希望通过系统的理论分析、计算机仿真及临床试验,减少个体眼球参数差异引起的测量误差,提高弥散斑验光的精度,并通过后续的设备改进实现自主、快捷验光,使其能够运用于临床筛查乃至专项检查。
3.1 误差分析和改进措施
系统误差源于简化模型眼和个体眼轴、节点参数的差异。在上述分析中,选用4 mm瞳孔直径和20 mmNO'长度使理论精度相对于前人的研究[6]有了较大的改进。后续的改进包括收集临床屈光不正患者的个体化参数,利用多因素线性回归修正表达式,提高验光准确度,并扩大适用人群范围。
患者的主观判断误差也不可避免。由于球差的存在,弥散斑周围有毛刺,这在一定程度上干扰了两个弥散斑相切的判断。瞳孔直径的选择是解决这个问题的关键,4 mm瞳孔直径可有效地减少、缩短毛刺,同时又能提供较大的误差允许范围,每3 mm判断误差只影响0.25 D。不得不提的是,由于现有的设备不能实现自动化,患者需要指挥验光者移动反光镜来移动弥散斑,这样医患配合不佳也是误差的来源。后续的工作是利用光点自动控制装置,使患者能自己控制弥散斑的移动,这样不仅能提高精度,也提高了效率。
如何放松调节是所有自动验光仪必须面对的问题。弥散斑验光仪利用暗环境和远距离视标,有效地减少了调节[7]。这在测量中也有体现,即患者不会出现弥散斑忽大忽小的情况。但我们不可能消除调节,因此调节的存在也是误差的来源之一。
在实际应用中,测量误差往往难以避免。由上所述,瞳孔参数的选择提供了3 mm的测量误差允许范围,因此影响较小。若能实现自动化,通过步进马达的转动量来计算距离,精度更高。
3.2 应用前景
国内目前的验光设备绝大多数是进口产品,动辄10来万元,需要高精度的机械传动和精密的光电转换系统,这使专业的验光流程在我国很难普及。弥散斑验光仪的主要构建只包括一个激光光源和控制反射镜二维移动的传动系统,在成本上很有优势。此外,由于原理简单,验光师只引导患者判断相切即可,不需要专业的培训,这一点在普通眼镜店尤为方便。综上所述,由于经济性和简便性,弥散斑验光仪十分适用于初级验光,为后续的验配提供可靠的依据。
对于弱视患者,弥散斑验光仪还有独特的优势。主觉验光中,验光师根据患者对精细视标的判断来进行下一步的验配。如果患者为弱视,主觉验光就比较难进行下去,需要额外的专业知识或设备,如检影、照相等。而弥散斑验光仪由于采用激光光源,即使是高度屈光不正患者也可以在视网膜上获得较大的光照度。理论上,患者此时只需要局部视野具有一定的空间分辨力即可判断相切。
由于不同屈光介质的不同程度的损害,患者眼底的弥散斑会呈现各种形态。我们可以尝试通过绘制患者眼底的弥散斑的具体形态来分析其哪个部分出现了损伤。
由于患者需要主观判断眼底弥散斑,我们还可以利用弥散斑验光仪对患者进行视觉分辨功能的分析和测定,如分析患者的视觉系统对模糊像的判断能力,从而得出患者潜在的最佳视力。
我们相信,随着研究的深入,弥散斑验光仪一定会在临床、科研中发挥作用。
[1] Obstfeld H. Optics in vision[M]. London: Butterwortth &Co Ltd,1978, 58-99.
[2] 李欣茹, 黄学平, 陶育华, 等. 屈光不正眼弥散斑变化的实验研究[J]. 眼科研究, 1992,01, 30.
[3] 张勇, 潘红飙, 万川. 角膜中央厚度与眼轴长度及眼屈光度的关系分析[J]. 安徽医药 2009, 13(8): 931.
[4] 李辉, 阎洪欣, 刘玉华. 青少年单纯性近视眼屈光度与角膜曲率及眼轴的相关性[J]. 眼视光学杂志, 2005, 7(2): 105-106.
[5] 陈玉冰, 赵刚平, 潘美容等. 近视眼角膜中央厚度、角膜中央屈光力及眼轴长度的测定分析[J]. 现代医院, 2004, 4 (6) : 8-9.
[6] 陶育华, 黄学平, 林冰, 等. 非正视眼离焦弥散斑的变化与特征[J].温州医学院学报, 1995, 2: 93-95.
[7] 瞿佳. 视光学理论和方法[M]. 北京: 人民卫生出版社, 2004
