地下结构地震反应分析中材料非线性的影响

单华廷，李立云，杜修力

（北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124)

0 前言

日本阪神地震后，地下结构的抗震问题逐渐引起土木工程界和地震工程界重视，并成为其研究热点。为保证地铁等地下结构在强地震作用下的安全运行，国内外学者利用各种方法对地下结构的地震反应问题进行了大量的研究，数值模拟方法以其高效、经济的特点被广泛应用。庄海洋等[1-2]、杜修力等[3-4]、郝志宏等[5]、Barbat等[6]、Hanganu 等[7]对地下结构抗震问题进行了研究，并取得了一些成果。在地下结构的抗震数值分析中，非线性问题对分析结果有重要的影响，不考虑这些因素可能带来较大的误差。非线性问题主要包括土与结构接触的非线性问题和材料非线性（土体材料和结构材料的非线性）问题，现有的研究成果中少有同时考虑这两类非线性问题。

本文应用大型通用有限元软件 ANSYS，基于杜修力等[8-9]提出的静动统一数值分析方法，对某地铁地下结构的地震反应进行数值模拟，分析在考虑接触效应和材料非线性特性时对地下结构的抗震反应影响。以期对地下结构地震反应分析中非线性因素的影响有较为清楚的认识。

1 静动统一数值分析方法

进行地震作用下地下结构的动力反应分析时，需要考虑地下结构在场地自重稳定场中产生的初始应力，一般将静力作用下的初始状态作为地震动力分析的初始条件。早期的研究中，静力分析过程一般采用固定边界，在动力分析时将静力分析得到的边界反力作为约束[10]，由于边界的不统一容易导致的误差不易判定，因此，杜修力等提出来解决这一问题的静、动统一数值分析方法[8]。静动统一数值分析方法是应用动力方法求解静力问题，求解思路是：在整个计算模型上设置黏弹性人工边界[11-12]，求得计算系统在介质自重下的静力稳定解。由于系统的阻尼作用，经过一定时间的震荡衰减，将趋于一个稳定的应力场，此时的应力场即可认为是系统自重引起的初始应力场，并且把这个稳定的应力场作为地震荷载作用的初始条件，进行系统在重力和地震荷载共同作用下的地震反应分析。

2 非线性问题的模拟

2.1 接触非线性问题

由于土体和地下结构两种介质的力学特性差别明显，强地震发生时，在土体与地下结构接触面处产生较大的相对变形，甚至会出现沿接触面法向相对分离和切向相对滑动的接触非线性问题。杜修力等[3]采用现有的大型有限元软件通用的接触面对法对其进行了模拟。接触面对法是接触力学方法的一种，也是有效处理接触问题的方法之一。有限元分析中，通过在土与结构的接触面处分别定义结构和土体为主、从接触面，通过主、从接触面之间的力学行为来模拟土与结构的动力接触特性。本文也采用这一方法。

2.2 材料非线性问题

为了较好地考虑材料的非线性特性，采用Drucker- Prager本构模型（简称D-P模型）来描述土体的力学特性，这种屈服准则考虑了静水压力对土体屈服面的影响。D-P模型屈服面见图1，应力-应变关系曲线见图2；混凝土本构关系采用Willam- Warnke五参数模型（简称W-W模型），其应力-应变关系按《混凝土结构设计规范》规定的公式进行拟合。W-W模型应力屈服面及混凝土应力-应变关系曲线如图3、图4所示。

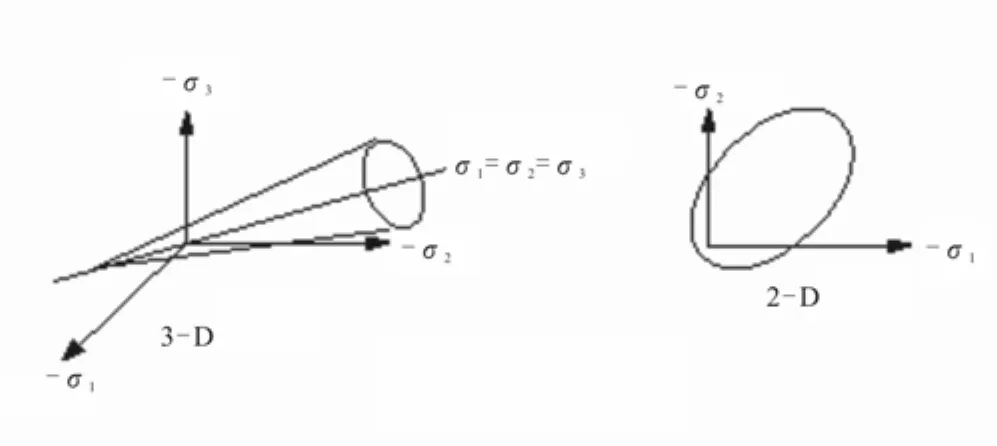
图1 土体D-P模型屈服面图Fig.1 The Yield surface of D-P constitutive model for soil.

3 算例分析

3.1 有限元建模

某地铁地下结构高8 m，宽19 m，中柱宽1 m，边墙厚1 m，顶板、底板厚1 m，顶板埋深5 m。计算区域宽度取67 m，深度取24 m。

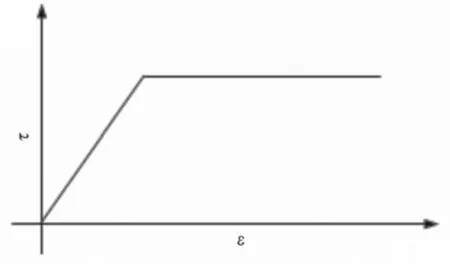
图2 土应力-应变关系曲线Fig.2 The Constitutive relation of soil.

图3 混凝土W-W模型屈服面图Fig.3 The Yield surface of W-W constitutive model for concrete.

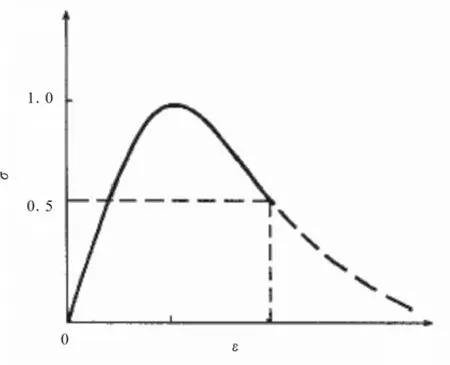
图4 混凝土应力-应变关系Fig.4 The Constitutive relation of concrete.

土体和地下结构分别进行网格划分，在土体与结构接触界面处定义接触面对来考虑二者之间的相互作用。由于土体和结构的刚度相差很大，采用刚体-柔体接触类型，其中结构面定义为主接触面(目标面)，土体面定义为从接触面(接触面)，接触初始状态为缝隙关闭，没有滑动。接触算法采用增广的拉格朗日乘子法。在计算时，初始法向接触刚度取为土体的刚度，并允许在计算中调整，切向刚度由摩擦系数和法向刚度共同确定，并随法向刚度的变化而变化。考虑到介质材料的能量耗散和应用的方便，在计算中考虑土体和结构的材料阻尼，阻尼比和其他的材料参数见材料参数表1（中柱的材料参数为折减后的参数），有限元计算模型见图5。

表1 材料参数表

图5 土-结构相互作用有限元计算模型Fig.5 Finite element mode of soil-structure interaction.

3.2 地震波输入

本文选用底部垂直入射的天津波(SV波)进行地震反应分析，采取在模型边界节点输入地震波等效节点荷载的波动输入方法，为了研究强地震对地下结构地震响应的影响，对天津波进行人工放大，分别取地震动加速度峰值为0.1 g、0.2 g和0.4 g。天津波的位移、速度、加速度时程曲线如图6所示。

3.3 数值计算结果分析

本文算例分别针对考虑土体介质与结构材料非线性和不考虑材料非线性两种情况进行了计算。控制节点的选取是根据应力、应变最不利位置原则综合考虑，分别考虑水平应力、应变，竖向应力、应变，剪应力、应变及mises应力、应变的最不利位置，结合地震调查结果，分别从地下结构顶板侧墙和中柱选取最不利节点位置进行分析，具体节点见图5。

3.3.1 地下结构应力、应变云图分析

图7、图8 分别为地下结构在天津波加速度峰值为αmax=0.2 g的地震作用下，在t=12.90 s时刻结构的应力、应变云图。从应力云图中可以看到，水平应力最不利位置为顶板中部外侧和底板的中部内侧左右，竖向应力最不利位置为右侧墙底部内侧和左侧墙顶部外侧， mises应力云图最不利位置为右侧墙底部内侧；而从应变云图中可以看到，中柱底部的塑性变形发展充分，处于危险的状态，是地下结构中的薄弱部位，与震害调查较为吻合。

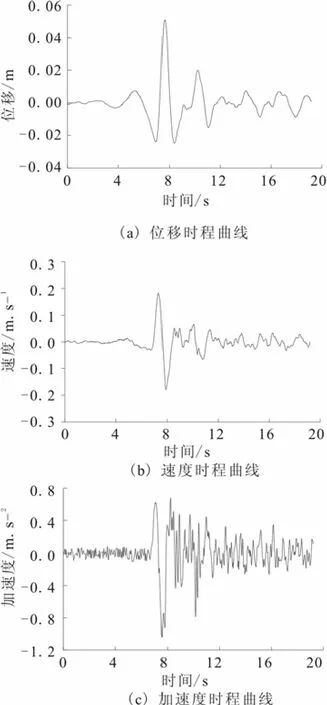
图6 天津波时程曲线Fig.6 Time history curves of Tianjin earthquake wave.

结构顶板和侧墙构成了典型的刚架体系，在重力和水平地震作用下，结构顶板是受弯构件，顶板跨中弯矩较大，水平拉、压应力、应变均出现较大值，在顶板端部负弯矩和剪应力也较大，故其水平应力、应变也会出现较大值；底板与顶板受力机理相同，不再另外说明；在侧墙顶部也出现较大端弯矩，侧墙出现竖向应力较大值；在中柱部分，底部压力较大，故其底部的压应力、应变都较大；随着地震作用的增大，应力、应变均增大，结构材料进入塑性状态，出现塑性应力重分布，且由于地震作用的反复作用，对地下结构不断的加载、卸载，塑性应变不断累积，出现较大的应变区域。

3.3.2 部分节点应变动力时程曲线分析

为了分析地下结构的塑性变形的发展状态，对各控制节点的应变进行动力时程分析，图9为部分控制节点应变动力时程曲线。从应变时程曲线中可以看到，考虑了材料的非线性特性后，在结构和中柱中各个节点都产生了塑性变形，但其规律并不相同，结构

中各节点的塑性应变发展占总应变相比很小，而在中柱中，塑性应变有了很大的发展，达到总应变的一半甚至和接近于总应变，表明中柱中塑性应变占较大大部分，塑性应变发展充分。

图7 t=12.90 s时刻结构的应力云图Fig.7 The stess distribution of the structure at t=12.90

图8 t=12.90 s时刻结构的应变云图Fig.8 The strain of the structure at t=12.90 s.

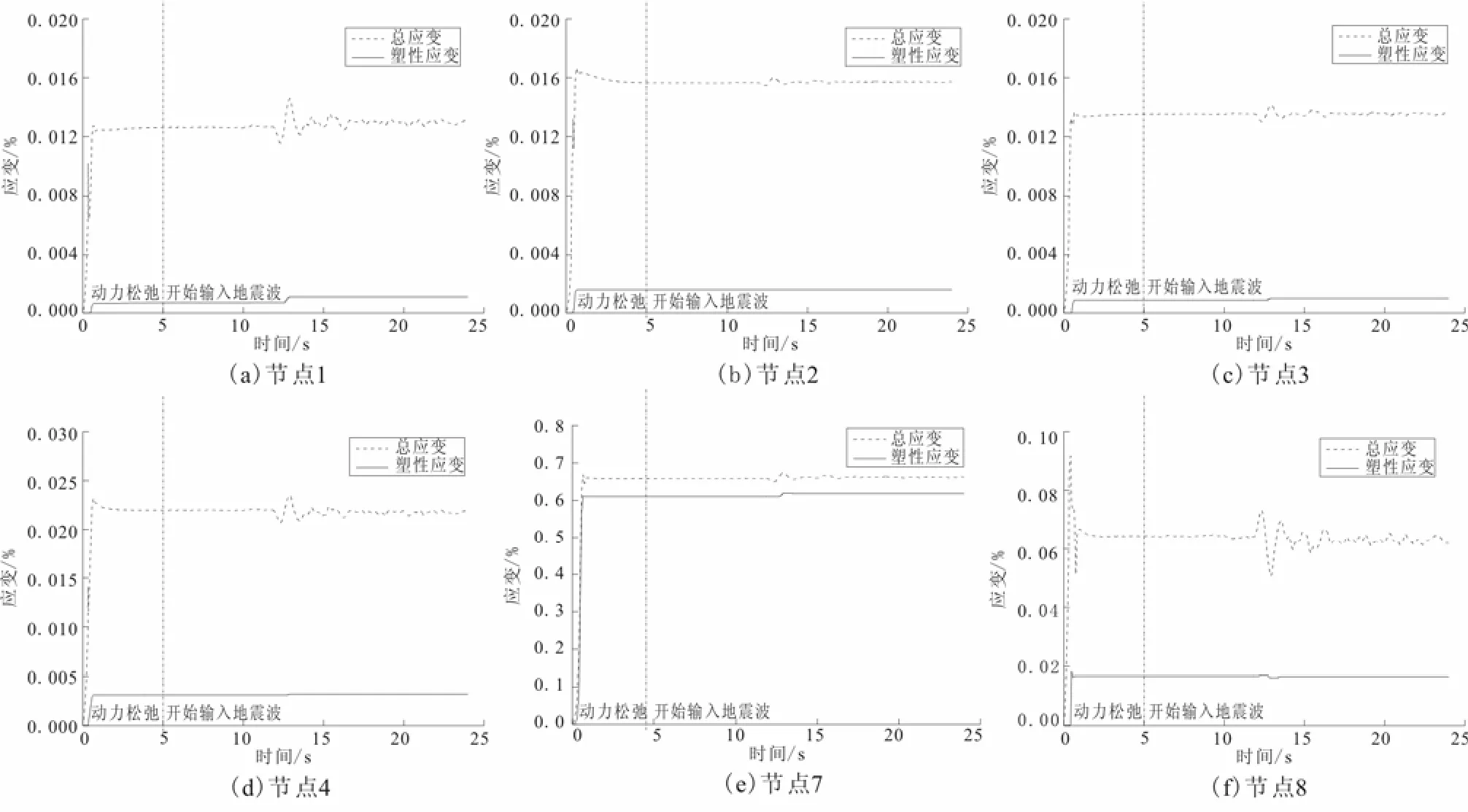
图9 部分控制节点应变时程曲线Fig.9 Dynamic time history curves of strain at some control nodes.

表2 不同地震动峰值条件下地下结构应力(MPa)

表3 不同地震动峰值条件下地下结构应变(%)

3.3.3 不同地震动峰值下应力应变对比

表2、表3为地下结构各节点在不同地震动峰值条件下的峰值反应，从表中数据可以发现，随着地震动加速度峰值的增大，地下结构的地震反应也增大，但不同部位对地震动的敏感程度并不相同：在结构中，顶板、底板增长较小，侧墙增长较大，表明地下结构侧墙对地震动的峰值条件较为敏感；在中柱中，底部增长较小，顶部增长较大，表明柱顶部对地震动峰值条件较为敏感。此外，结构和中柱顶部节点的应力、应变增幅明显，现象一致，表明结构在较低地震条件下没有达到屈服，应力、应变随着地震动峰值的增大增大；而中柱底部应力基本不变、应变继续增大，表明在较低地震条件下中柱底部接近破坏，是薄弱部位。

3.3.4 材料非线性对计算结果的影响

计算结果表明，考虑土与结构材料的非线性后，对控制节点的位移、速度、加速度影响不大，而对控制节点的水平应力、竖向应力、剪应力及mises应力影响较大，改变了最不利位置，甚至出现了节点应力拉、压状态发生改变。本论文仅就应力、应变结果进行分析，表4～表7分别为地下结构在αmax=0.2 g的地震作用下t=12.90 s的最不利峰值应力、应变数据表。

表4 结构最不利位置峰值应力

表5 结构最不利位置峰值应变数据表(%)

表6 中柱最不利位置峰值应力

表7 中柱最不利位置峰值应变数据表(%)

通过上表中数据可以看到，考虑材料非线性特性后，地下结构的地震反应明显发生变化，尤以应变增大显著，但结构和中柱的反应有所不同：在结构中最不利位置的应力、应变都有明显的增大作用；中柱最不利位置应力均减小明显，但应变却表现为不同的现象，从非线性应变时程曲线分析可以看出，此处出现了产生塑性应变，并达到了屈服。

总之，不考虑材料的非线性特性时地下结构的地震反应偏小，在地下结构抗震设计中偏于不安全，因此，在地下结构抗震设计中需要采取相应的措施，保障地下结构的抗震安全。

4 结论

本文基于粘弹性人工边界和静动统一数值分析方法的求解思路，利用大型通用有限元软件 ANSYS模拟了接触考虑材料非线性行为的地下结构地震反应，并且得到了比较合理的计算结果，在此基础上与不考虑材料非线性行为的结果进行对比，得出以下结论：（1）考虑材料的非线性特性后，地下结构的动力反应显著增大，部分节点应力、应变峰值甚至增大到十几倍；（2）应力、应变最不利节点位置发生了改变；（3）节点应力拉、压状态发生改变，出现了交变内力；（4）地下结构反应随着地震动峰值的增大而增大；（5）对节点的位移、速度、加速度有增大作用，但影响不大。

[1]庄海洋, 程绍革, 陈国兴. 阪神地震中大开地铁车站震害机制数值仿真分析[J]. 岩土力学, 2008, 29(1): 246-250.

[2]庄海洋. 土-地下结构非线性动力相互作用及其大型振动台试验研究[D]. 南京: 南京工业大学博士学位论文, 2006.

[3]杜修力, 赵源, 李立云. 土体-结构界面接触对地下结构动力反应的影响[J]. 防灾减灾工程学报, 2010, 30(5): 471-478.

[4]赵源, 杜修力, 李立云. 地震动入射角度对地下结构动力反应的影响[J]. 防灾减灾工程学报, 2010, 30(6): 625-630.

[5]郝志宏, 叶英华, 刘运亮, 等. 基于ANSYS的北京某明挖地铁车站抗震分析[J]. 工业建筑, 2008, 39(增刊): 752-758.

[6]Barbat A H, Oller S, Onate E, et al. Viscous damageModel for timoshenko beam structures[J]. International Journal of Solids and Structures, 1997, 34 (30): 3953-3976.

[7]Hanganu A D, Onate E, BarbatAH. A finite element methodology for local/global damage evaluation in civil engineering structures[J].Computers and Structures, 2002, 80(12): 1667～1687.

[8]杜修力. 工程波动理论与方法[M]. 北京: 科学技术出版社, 2009.

[9]廖维张, 杜修力, 赵密, 等.开放系统非线性动力反应分析的一种算法[J]. 北京工业大学学报, 2006, 32(2): 115-119.

[10]杜修力, 涂劲, 陈厚群. 有缝拱坝一地基系统非线性地震波动反应分析方法[J]. 地震工程与工程振动, 2000, 20(1): 11-20.

[11]杜修力, 赵密, 王进廷. 近场波动模拟的人工应力边界条件[J]. 力学学报, 2006, 38(1): 49-56.

[1]刘晶波, 谷音, 杜义欣.一致粘弹性人工边界及粘弹性边界单元[J].岩土工程学报, 2006, 28(9): 1070-1075.