考虑土－结构相互作用的风力发电机塔架地震响应分析①

2011-10-16曹青，张豪

地震工程学报 2011年1期

关键词：风轮塔架风力机

曹青，张豪

（河海大学水利水电工程学院，江苏南京 210024）

考虑土－结构相互作用的风力发电机塔架地震响应分析①

曹青，张豪

（河海大学水利水电工程学院，江苏南京 210024）

利用有限单元法建立用弹簧阻尼单元近似模拟土－结构相互作用的风力发电机塔架结构模型。采用更新的拉格朗日增量有限元格式，逐步积分的Newmark法求解，通过算例分析了多维地震荷载作用下风力机塔架结构的时程响应规律，研究了P－Δ效应、竖向地震作用和土－结构相互作用的影响。分析得出：土－结构相互作用对风力发电机塔架结构的地震动力响应的影响不容忽视，在材料线弹性范围内竖向地震荷载和P－Δ效应对结构的动力特性影响较小。

地震响应；风力发电机塔架；P－Δ效应；土－结构相互作用

Abstract：Using finite element method，a FEM model of wind turbine tower considering soilstructure interaction simulated by the spring－damping element is proposed to investigate its dynamic response under multi－dimension seismic excitation in time domain.The updated Lagrange FEM formalism is adapted to discrete the equation and to use Newmark integral method to solve it step by step.Through this numeral analysis on the influence of P－Δeffect，the effects of soil－structure interaction and vertical seismic action on structure＇s dynamic property，the time－history response rule for the tower is studied with a real example.The result show that the effect of the soil－structure interaction on the seismic response of wind turbine tower structure is significate and should not be ignored.In line elastic range，the influence of vertical seismic loads and the P－Δeffect are not notable.

Key words：Seismic response；Wind turbine tower；P－Δeffect；Soil－structure interaction

0 引言

近年来风力发电以其技术成熟，无污染和可再生性得到迅猛的发展。越来越多的风力机建在地震活跃区域，对风力发电机塔架结构抗震研究对保证结构稳定、安全生产具有重要的理论意义及实用价值。

风力发电机主要是由捕捉风能的转动的风轮、重量比较重的近似刚体的机舱、轮毂和底座、起支撑发电机上述部分的高耸大柔度的塔架结构及地基组成，属于一个多体组合不对称的高耸结构。在结构的地震响应分析中，土与结构的相互作用是必须要考虑的，因为在地震中的风力机结构的动力行为受到地基、基础耦合作用的影响是巨大的［1］。在所有结构中，塔架结构的地震动力响应一般最大，且其支撑了风力机重要的动力部件，在地震中不能倾覆和倒塌，因而保证塔架的强度与稳定性是最重要的。

风力机塔架系统是各部分耦合在一起的三维系统，影响其地震作用下的动力响应的因素也是众多的。首先地面运动是复杂的三维空间运动，水平双向分量又有竖向方向分量。有研究表明［2－4］高耸结构特别是烟囱、水塔等结构，其破坏是由水平和竖向地面运动共同作用引起的。又由于风力机塔架及叶片是一高耸长细悬臂结构，结构质量分布又不均匀，在结构系统动力分析中必然包括荷载作用下结构的变形二阶效应（P－Δ效应）［4－5］，因此需要研究P－Δ效应对风力机结构地震响应的影响。

目前已有一些风力机塔架地震响应的分析成果。文献［6－7］都采用多体动力学模型，以弹簧、阻尼模型考虑SSI的影响，分析了风力机塔架地震时程响应；贺广零［8］还建立了一体化的风力机有限元模型，在基础底部设置弹簧阻尼来考虑SSI的影响，并对风力发电机塔筒系统进行了模态和地震时程响应分析。综合文献可以看出，目前对风力机塔架的地震响应分析还不够系统全面，还没有对P－Δ效应以及竖向地震作用影响的研究，因而开展考虑土－结构相互作用风力发电机塔架地震响应的深入研究是有必要的。

本文应用三维有限单元方法，用弹簧阻尼系统模拟土－结构的相互作用，采用更新的拉格朗日增量格式，考虑P－Δ非线性效应，用逐步积分的Newmark方法进行分析，研究结构在地震作用下的时程响应特性以及各种因素对结构地震响应动力特性的影响。

1 基本理论

1.1 土－结构的相互作用模型

通常用有限元方法进行地基土与结构的复杂相互作用分析仿真耗时较长。能抓住地基土与结构的相互作用重要特征的一个有效方法为用弹簧阻尼系统表征土与地基的相互作用。对于三维的土壤基础模型，在水平平面内的平动分量与转动分量是耦合在一起的，但其耦合量比较小，通常将其忽略，尤其对于在浅层地基上的风力发电机基础。因而将所有运动分离单独考虑。对于刚性圆盘基础，就是分别在各向加弹簧和阻尼器，其常数［9］如下：

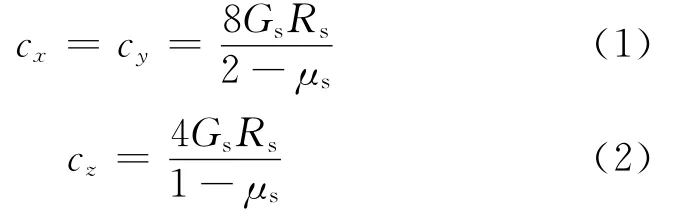
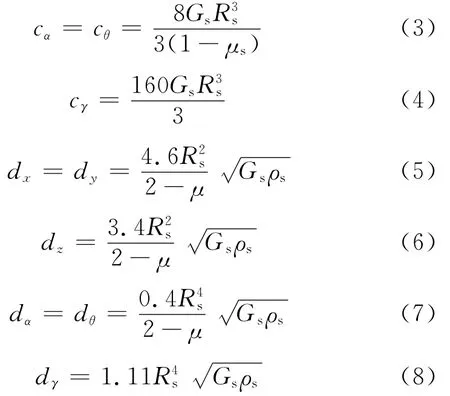
式中：cx、cy和cz分别表示水平x、y向和竖向z向刚度系数；cα、cθ和cγ分别表示地基转动和对竖轴扭转刚度系数；相对应的di（i＝x，y，z，α，θ，γ）代表阻尼系数；Rs是刚性圆形基础的半径；Gs、μs和ρz分别是土壤的剪切模量，泊松比和密度。

因而，由土与结构的相互作用引起的力可以写为

这力和力矩作为荷载加到模型运动控制方程中。

1.2 P－Δ效应模型［10－11］

在结构反应中，所谓的P－Δ效应主要是指竖向荷载作用下，由于水平位移所附加的对结构反应的影响，即变形的高价分量。由增量应变

其中：

式（11）中后一项是位移的高阶微量，即P－Δ影响。采用更新的拉格郎日格式，以几何刚度的形式加以考虑，多自由度体系一般弹性动力方程用增量可以表示为

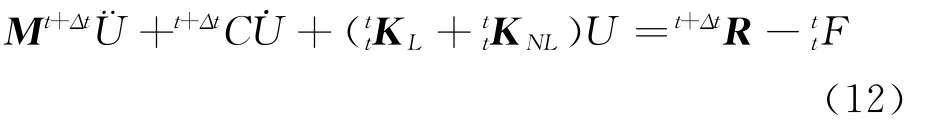
其他矩阵和线性结构一样，只是加了非线性应变引起的几何刚度矩阵，而且在荷载中考虑了前时刻的内部节点力。其中非线性刚度矩阵表示为

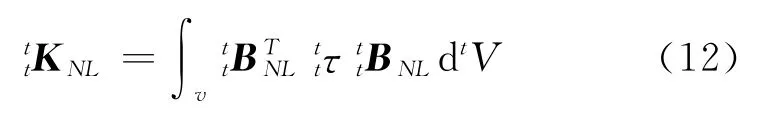
其中

h为形函数。

每个时步都由前一时步值形成线性非线性刚度矩阵，用Newmark方法逐步积分进行求解，从而得到考虑二阶效应的几何非线性的解。

2 数值分析

2.1 模型建立

以某一1.0MW风力发电机［12］为例进行研究。该发电机为三叶片上风向水平轴风力发电机，额定功率1.0MW；轮毂高度处额定风速13m／s；风轮直径62.00m；风轮额定转速18.8r／min；风轮（叶片和轮毂）重量17 200kg；叶片重量4 400kg；机舱重量49 300kg。风轮和机舱重心偏离塔架中心1.2 m，风轮的旋转转动惯量为：2.8×106kg·m。塔架为圆锥筒型薄壁钢结构，塔架高度58m；底部直径3.5m；顶部直径1.8m；壁厚0.02m；材料为Q235－B；弹性模量E＝2.1×1011Pa；泊松比＝0.3；密度为7 850kg／m3；材料许用应力［σ］＝235MPa。

地基为三类地基，土壤假设为各向同性材料，材料常数为：剪切模量Gs＝5.6×106Pa；泊松比＝0.333；密度为1 900kg／m3。

研究采用大型商业软件ADINA对风力发电机塔架系统进行建模分析。因为风力发电机塔架属于细长杆件，塔筒直径由上向下逐渐变大，其作用机理更像三维的梁。为了能有效地抓住结构的主要特征又能减小计算量，所以采用6段不同尺寸的三维2节点的管单元进行模拟；转动的风轮用刚性的圆盘模拟，为三维的实体单元；轮毂采用集中质量模拟；机舱刚度较大，把它看做一个整体，用弹性模量较大的梁单元进行模拟；风轮与机舱、机舱与塔架间采用刚性连接；塔架底部设置弹簧阻尼单元。有限元模型及坐标系统见图1。

图1 风力发电机塔架有限元模型Fig.1 FEM model of wind turbine tower.

地震作用破坏力大，为研究地震作用的影响，考虑重力和静风荷载作用，不考虑脉动风荷载的影响。风力发电机处于正常运行设计工况，结构处于线弹性状态，模型采用Raleigh阻尼，阻尼比取2%。

地震动很复杂，与场地地震烈度和土壤性质有很大关系［13－14］。为了便于重点研究，地震波选用EI－Centro地震波，持时50s，其东西向分量加速度峰值210.12cm／s2，卓越周期0.50s，最大幅值出现在12.46s；南北向分量加速度峰值350.1cm／s2，卓越周期0.68s，最大幅值出现在3.14s；竖向分量加速度峰值245.2cm／s2，卓越周期0.119s，最大幅值出现在2.0s。地震波x轴正向加EW分量，y轴正向加NS分量和z向加竖向地震波分量。

计算模型情况有：无相互作用＋三向地震，相互作用（用弹簧阻尼单元考虑土与结构相互作用）＋三向地震，相互作用＋三向地震＋P－Δ效应，相互作用＋x、y两向地震作用（无竖向地震作用）。

2.2 自振特性

自振频率和振型是结构的基本的属性，表1给出三种计算情况的结构的自振频率。

由表1可以看出，各种情况下塔架系统的自振频率都高于风轮的旋转频率（0.313Hz）。考虑土壤与结构相互作用，结构的自振频率降低，其第一阶和第二阶模态分别为塔架横向（y向）顺风向（x向）模态，频率降低5%左右，第三阶主要为风轮绕轴转动，受地基影响很小，后面几阶为塔架扭转和弯曲振动的高阶振型，受地基的影响更大，能达到14.3%，因而在设计中要给予特别的关注，尤其对于软基。

表1 结构的自振频率（Hz）

考虑初始应力（几何刚度）（P－Δ效应影响）模型与考虑土与结构相互作用模型的结构自振频率比，各阶频率也有所下降，但影响很小，其顺风向（x）弯曲振动频率也只下降了1.6%，尤其对于高阶振型其影响更小。

2.3 动力响应分析

地面运动是非常复杂的，水平方向不仅是双向的，同时还有扭转的运动。因扭转运动记录资料很少，在本算例中不做考虑。主要考虑水平双向和竖向地震荷载。各计算工况时程结果见表2，及图2～图4。

图2 塔架底部的内力Fig.2 Interior force at tower foot.

图3 塔架底部的力矩Fig.3 Interior moment at tower foot.

图4 塔架顶y向位移Fig.4 Y－displacement at tower top.

（1）表2和图2、3是考虑土与结构相互作用下的结果，可以看出，风力机系统在三向地震作用下塔架结构主要以横风向（y向）和顺风向（x向）弯曲振动为主，且弯曲振动频率接近塔架的第一阶自振频率。由地震作用引起的塔架剪力比较小，且其高频成分比较多。塔架轴力比较大，主要因其静力结果较大。塔架竖向振动以高频振动为主，因为塔架竖向自振频率较高。水平两个方向的弯矩都比较大，绕竖轴的塔架扭矩比起弯矩来说较小。但对于风轮的主轴来说，由于受到旋转风轮的影响，其竖向剪力和扭矩比较大，因而在地震中主轴易被折断和引起塔架较大的偏航扭矩。总体来看各响应值在10s之前达到最大值，随后逐渐衰减。

表2 各工况下结构地震响应最大值

（2）图4和表2可以看出，土与结构相互作用对结构的动力响应影响很大，塔架顶部位移增加了10%，其相对挠度达到7.4‰，但其各内力都有所下降，主要因为地基软，柔度大，因而有可能使得像塔架这样的高耸结构在强度满足要求的情况下而失去稳定，发生倾覆倒塌事件。

（3）由于初始应力和变形影响了整体结构的刚度矩阵，每一个时步段都考虑这种应变的高阶微量，即考虑作用荷载P－Δ效应。由计算结果表2和图3、4可以看出，P－Δ效应引起了结构自振频率降低，结构地震响应周期延长，峰值有所增加，但影响比较小，P－Δ效应不显著。形成这种情况是因为地震作用下结构的动态变位过程十分复杂，过程中竖向力产生的附加弯矩在结构的某些部位可以和水平地震力、竖向地震力产生的弯矩反号；再者，对高耸结构而言地震反应中的高振型含量丰富，那种波形变形会使各质点重量对体系下方部位产生的附加弯矩也出现反号现象。上述两种情况都会减弱PΔ效应。

（4）竖向地震对位移和弯矩的影响很小，其作用和P－Δ效应作用近似。但对塔架轴力和风轮主轴竖向剪力影响比较大，塔架轴力增大25%左右，这对于高耸的塔架结构侧向稳定也是不利的，而且风轮主轴竖向剪力增大17%左右，这容易引起主轴被折断。

3 结论

由上述分析可以得出如下结论：

（1）风力发电机结构系统是一个不对称的结构，多向地震作用对结构的影响很大，不仅使塔架结构弯矩、挠度响应增大，容易引起塔架的倾覆，而且还使得风轮主传动轴有比较大的偏航方向及竖向的剪力，容易引起传动主轴折断。

（2）土与结构的相互作用使塔架结构各阶自振频率下降，尤其对高阶频率影响更大；使塔架内力减小，塔架挠度增大，容易引起风力机塔架的倾覆。因而对软基上的风力塔架抗震设计中更需要考虑土与结构的相互作用。

（3）P－Δ效应引起了结构自振频率降低，地震响应周期延长，振动幅值有所增加，衰减慢，但总体影响很小，若结构设计合理，P－Δ效应可以不考虑。

（4）竖向地震作用对结构响应影响就其量级来说比较小，主要引起结构竖向方向的惯性力增大，容易引起风轮主传动轴的的破坏和加剧高耸塔架侧向失稳的危险性。

［1］沈聚敏，等.抗震工程学［M］.北京：中国建筑工业出版社，2000：247－258.

［2］朱春良，杨春田，于淑琴，等.烟囱竖向地震响应的试验与研究［J］.特种结构，2002，19（3）：34－37.

［3］陈健云，周晶，马恒春，等.高耸烟囱结构竖向地震响应的模型试验研究及分析［J］.建筑结构学报，2005，26（2）：87－93.

［4］张玉梅，朱玉普，张晓东.多向地震耦合作用下高耸结构土－结构动力相互研究［J］.工程力学，2008，25（2）：154－159.

［5］刘铁林，姜迎春，刘伟.地震作用下高耸结构动力响应波动分析方法［J］.工程力学，2008，25（增刊Ⅱ）：164－167.

［6］ Zhao X，Maiβer P.Seismic response analysis of wind turbine towers including soil－structure interaction［A］∥Proc.IMechE［C］.220Part K：J.Multi－body Dynamics，2006：53－61.

［7］贺广零.考虑土－结构相互作用的风力发电高塔系统地震动力响应分析［J］.机械工程学报，2009，45（7）：87－94.

［8］贺广零，周勇，李杰.风力发电高塔系统地震动力响应分析［J］.工程力学，2009，26（7）：72－77.

［9］ Wolf J P.Spring－dashpot－mass models for foundation vibrations［J］.J.Earthq.Eng.Struct.Dyn.，1997，26：931－949.

［10］ Klaus－Jǔrgen Bathe.Finite Element Procedures［M］.Upper Sandle River，New Jersey：Prentice－Hall，1996：485－575.

［11］爱德华·L·威尔逊著.北京金土木软件技术有限公司中国建筑标准设计研究院译.结构静力与动力分析［M］.北京，中国建筑出版社，2006：101－110.

［12］李声艳.大型风力发电机组的动力学特性计算分析［D］.天津：天津工业大学，2007.

［13］王恒知，石玉成，卢育霞，等.人工拟合地震动时程参数对场地反应的影响分析［J］.西北地震学报，2009，31（2）：126－ 130.

［14］王国波，杨林德.上海软土自由场地的三维地震响应分析［J］.西北地震学报，2008，30（4）：27－31.

Seismic Response Analysis of Wind Turbine Tower with Soil－Structure Interaction

CAO Qing，ZHANG Hao

（College of Water Conservancy and Hydropower Engineering，Hohai University，Nanjing 210098，China）

TU311.3