用SAS软件实现成组设计定量资料的统计分析

胡良平,郭辰仪(军事医学科学院科技部生物医学统计学咨询中心,北京100850)

上期介绍了配对设计定量资料的一般处理方法,所处理的数据存在某种一一对应的联系,例如同一批对象试验前后的数据。但在有些试验中,有时很难找到满足配对要求的样本,例如想要比较两种药物治疗效果的优劣,但两种药物作用在同一个病人身上会相互影响。最恰当的方法就是选择病情相近的病人若干,随机分成两组,分别接受不同药物治疗,比较最终治疗效果。对于这样的问题,需要采用成组设计资料的分析方法。下面看一个例子。

例1 某试验研究一种药物治疗急性脑出血的疗效,试验前进行临床病史资料收集和CT检查,选取符合标准者,并随机分组。为确保对照组和治疗组病人条件一致,排除非试验因素干扰,分别测定治疗前两组病人的出血量,如表1所示[1]。

类似例1的问题在临床科研中经常会遇到。如果两组对象在基线水平上存在差异,那对于试验结果会产生很大的影响,导致试验结果的不可信。分析两组定量数据均值之间的差异是否具有统计学意义,可采用成组设计定量资料假设检验方法进行统计分析。

1 成组设计

1.1 成组设计的定义和特点 试验中,如果只涉及一个具有两水平的试验因素,即受试对象接受两种不同的处理,而无法采用配对设计时,可采用成组设计。若试验因素独立于受试对象,成组设计将全部受试对象完全随机地均分入该试验因素的两个水平组中,即采用完全随机的方法分配受试对象;反之,将从两个特定的子总体中随机抽取受试对象。像这样,观测两组受试对象接受不同处理后,比较某一观测指标之间差异的试验安排方法,称为成组设计。成组设计的正规名称为单因素两水平设计。

成组设计的特点是:仅涉及一个试验因素,且该试验因素只有两个水平,未对其他任何重要非试验因素进行有计划的安排,希望通过随机化分组或随机抽样来平衡所有非试验因素在两组间对观测结果的干扰和影响。常见成组设计包括一元定量/定性资料成组设计和多元定量/定性资料成组设计,本文仅对定量资料成组设计进行分析解释。

1.2 成组设计定量资料统计分析方法的合理选用 (1)确定试验仅受一个因素影响,且所观测值为定量数据;(2)检测两组定量资料是否分别满足正态性要求,若满足则采用t检验(方差不齐时采用近似t检验);若有任一组定量资料不满足正态性,则采用秩和检验。(3)当检测的是在专业上有联系的多个定量指标时,需采用成组设计定量资料多元方差分析。

2 实例解析

2.1 应用 SAS软件分析成组设计一元定量资料 例2 沿用例1中的资料,试问两组受试对象治疗前的平均出血量之间的差异是否有统计学意义?对问题的分析与SAS实现 此资料仅有两组病人,涉及一个具有两水平的试验因素。两个水平分别为“对照组”和“试验组”;只有一个定量指标为“出血量”,两组数据相互独立,不存在关联关系,故此定量资料属于成组设计一元定量资料。对两组病人的出血量分别进行正态性检验,若都服从正态分布,可采用成组设计一元定量资料的 t检验;反之,可采用成组设计一元定量资料的秩和检验。应用SAS进行分析,程序如下。表中数据以空格隔开,换行无要求;注意每组水平标志后的数据个数要与实际相符,否则程序会出错。

/＊第1步导入数据＊/ data a; input group＄n; do i=1 to n; input x@@; output; end; cards; first 20 31.31 30.85 3.43 36.26 16.30 20.54 0.43 19.91 12.76 16.36 27.05 12.93 31.67 30.87 19.65 31.60 15.39 31.69 20.25 4.765 second 26 5.80 31.04 8.28 16.49 28.83 24.74 13.53 26.82 14.06 20.49 5.75 11.59 22.83 47.27 41.03 32.65 37.70 30.42 27.81 6.65 2.84 47.18 30.18 22.60 19.52 46.38 ; run; /＊第2步正态性检验＊/ proc univariate normal noprint; var x;by group;

output out=AAA normal=W probn=P; run; ods html; /＊第3步输出正态性检验结果＊/ proc print data=AAA noobs; var group W P; run; /＊第4步输出t检验结果＊/ proc t test cochran data=a; class group;var x; run; /＊第5步输出秩和检验结果＊/ proc npar1way wilcoxon data=a; class group; var x; run; ods html close;

程序说明:第1步建立数据集,“input”语句表明从数据cards中读取相应的数据赋值给变量;“group”用来标记数据x是属于哪个组;“n”表示每个组的数据数分别是多少。第2步调用univariate过程,对数据资料进行正态性检验;“noprint”选项表明不需要输出结果;后面在第3步中会提取这部分的结果精简输出。观察第3步结果,当两组数据都满足正态性的前提下,进行第4步t检验。若有任何一组数据不满足正态性,则略过第4步结果,查看第5步结果。另外,ods html语句用来将统计分析结果输出成网页格式。

以下为SAS输出结果及结果解释。

第3步输出:

组别 W P第1组 0.927 56 0.138 57第2组 0.956 38 0.325 33

从结果可以看到,第1组和第2组正态性检验P值均＞0.05,因此可采用第4步的t检验(若不满足正态性,请参看例3非参数检验输出结果)。

第4步输出:

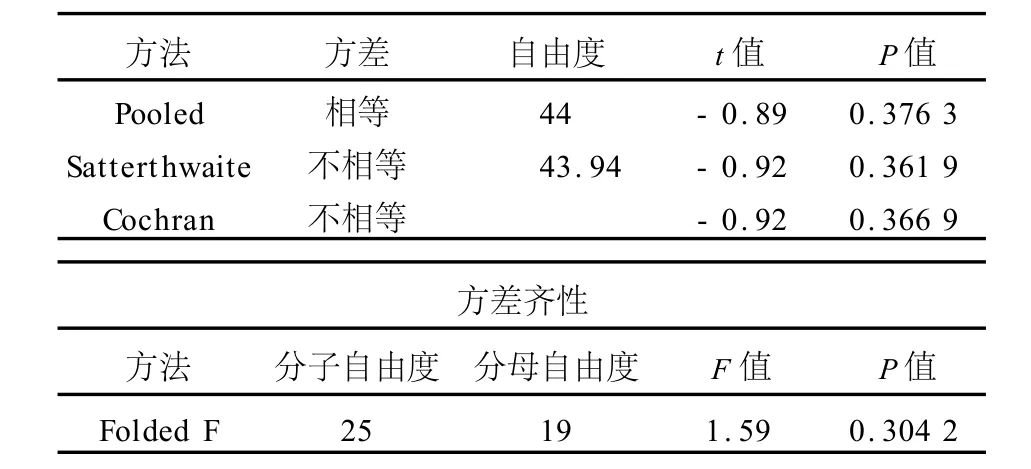
SAS系统t检验过程

由方差齐性检验结果可知,P值为0.304 2＞0.05,因此认为两组数据所对应的总体方差相等。在t检验结果中,参看方差相等的检验方法Pooled即可。t检验结果,P=0.376 3＞0.05,所以可以认为两组数据之间的差异无统计学意义。本例中参看第4步结果即可,下面将第5步结果也展示出来:

SAS系统NPAR1WAY过程

如果上面两组有任何一组不满足正态性,则需参看这部分输出结果。这是在成组设计一元定量资料秩和检验统计量基础上,采用两种近似检验方法(正态近似法与t近似法)求出近似检验统计量的 Z值和P值。若此处“Two-SidedPr＞|Z|”的 P＜0.05,则可认为两者之间有显著性差异。统计结论: Z=-0.587 2,P=0.557 1＞0.05,故按α=0.05水准,认为两组出血量的平均值之间的差异无统计学意义。专业结论:因两组病人治疗前出血量可认为基本相同,当出血量被认为是对试验结果唯一的重要非试验因素时,这两组病人之间的均衡性很好,可以接受不同水平的试验因素的处理。

2.2 应用 SAS软件分析成组设计多元定量资料 上面的例子中只涉及到一个定量观测指标,当有多个在专业上有联系的定量观测指标时,则需要采用成组设计定量资料多元方差分析方法,联合考查两组受试者在多个定量指标的平均值(称为均值向量)之间的差异是否具有统计学意义。

例3 比较帕罗西汀治疗单纯抑郁症和抑郁合并焦虑症病人的疗效[2],选取2003年8月-12月在上海几所三级甲等综合性医院就诊的抑郁症病人。在基期时已服用与未服用帕罗西汀的病人的各项SF-36评分数据见表2(本文为突出显示SAS分析方法[3],仅选取其中两项指标),试问这些病人是否能被共同用于试验研究,还是要区分开试验?

对问题的分析与SAS实现 例3中测量两个定量指标,有两组受试对象,属于成组设计二元定量资料,采用成组设计定量资料二元方差分析,实现此分析的SAS程序如下。表中数据以空格隔开,换行无要求;注意每组编号后的数据个数 n要与实际相符,否则程序会出错。受文章篇幅限制,此处略去一些数据,用“…”表示。

表2 病人在基期的生活质量aTable 2 Patients’quality of life before treatment

/＊第1步导入数据＊/ data b; input group＄n; do i=1 to n; input x1 x2@@; output; end; cards; first 20 75.23 29.57 75.27 30.22…second 18 83.22 30.70 78.81 31.12…; run; /＊第2步方差分析＊/ ODS html; proc glm; class group; model x1 x2=group/ss3 nouni; manova H=group; means group; run; ODS html close;

程序说明:程序中第1步是数据步,“x1”和“x2”分别代表两个指标生理功能A和生理功能B;第2步是过程步,是二元方差分析过程步,调用一般线性模型过程(GLM过程)对“x1”和“x2”进行二元方差分析,“ss3”表示应用 GLM过程中第3种算法。此过程中“manova H=group”语句是进行多元方差分析,以分组为影响因素进行分析。

SAS输出结果及结果解释:

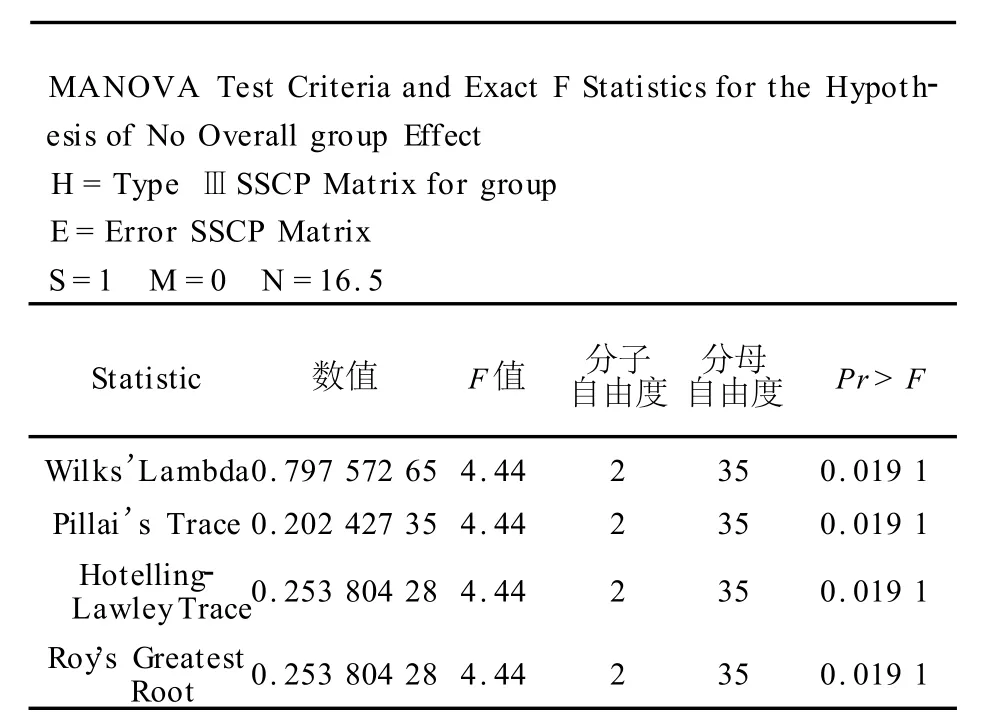
SAS系统一般线性模型过程多元方差分析

这部分给出了成组设计定量资料二元方差分析结果,同时考虑两项指标,采用了4种统计分析方法,通常只看第1种。Wilks’λ=0.798,对应的F=4.44,分子和分母自由度分别为2和35,对应的P=0.019 1＜0.05,说明就两个指标整体而言,两组数据的均值向量之间的差异有统计学意义。

专业及统计结论:针对两个指标整体而言,基期时已服用与未服用帕罗西汀病人的各项SF-36评分数据存在差异,其差异有统计学意义(Wilks’λ= 0.798,F=4.44,P＜0.05)。因此,两组病人的两项定量指标的平均水平不等,故不适合把它们放一起进行该试验,需在不同组内分别进行。

[1] 陆 磊,孙晓江,张 进,等.盐酸甲氯芬酯治疗急性脑出血的疗效评价[J].药学服务与研究,2007,7(4):271-273.

Lu Lei,Sun XiaoJiang,Zhang Jin,et al.The clinical efficacy of meclofenoxate hydrochloride in treatment of patients with acute intracerebral hemorrhage[J].Pharm Care Res,2007,7 (4):271-273.Chinese with abstract in English.

[2] 周学东,陈兴宝,季建林,等.帕罗西汀治疗单纯抑郁症和抑郁合并焦虑症病人的疗效比较[J].药学服务与研究,2007,7(2): 90-93.

Zhou XueDong,Chen XingBao,Ji JianLin,et al.Comparison of the efficacy of paroxetine in treatment of pure depression and depression combined with anxiety[J].Pharm Care Res,2007,7 (2):90-93.Chinese with abstract in English.

[3] 胡良平.医学统计学:运用三型理论分析定量与定性资料[M].北京:人民军医出版社,2009:40-85.

Hu LiangPing.Medical statistics-analysis of quantitative and qualitative data with triple-type theory[M].Beijing:People’s Military Medical Press,2009:40-85.Chinese.